> states<- as.data.frame(state.x77[,c("Murder", "Population","Illiteracy","Income","Frost")])
> fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
> confint(fit)
2.5 % 97.5 %
(Intercept) -6.552191e+00 9.0213182149
Population 4.136397e-05 0.0004059867
Illiteracy 2.381799e+00 5.9038743192
Income -1.312611e-03 0.0014414600
Frost -1.966781e-02 0.0208304170
> #结果表明,文盲率改变1%时,谋杀率就在95%的置信区间[2.38,5.90]中变化。另外,因为Frost的置信区间包含0,所以可以得出结论:当其他变量不变时,温度的改变与谋杀率无关。
标准方法
>fit <- lm(weight~ height, data=women)
> par(mfrow=c(2,2))
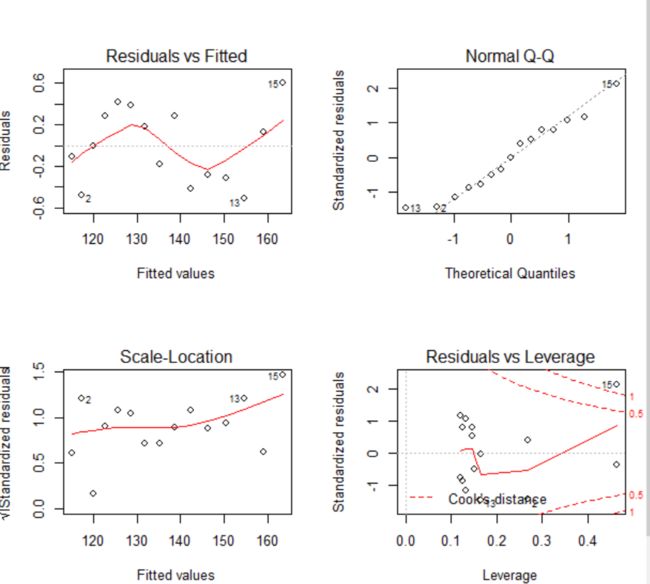
> plot(fit) #结果如下图
正态性 当预测变量值固定时,因变量成正态分布,则残差值也应该是一个均值为0的正态分布。正态“Q-Q,右上”是正态分布对应的值下,标准化残差的概率图。拖满足正态分布,那么图上的点应该落在呈45°的直线上;否则,就违反了正态性的假设;
线性 若因变量和自变量线性相关,模型应该包含数据中所有的系统方差。在“残差图与拟合图,左上”中可以清楚地看到一个曲线关系,暗示着可能需要对回归模型加上一个二次项。
同方差性 若满足不变方差假设,那么“位置尺度图,左下”中,水平线周围的点应该随机分布。
残差与杠杆图(右下),提供了可能关注的单个观测点的信息,从图形中可以鉴别出离群点,高杆杠点和强影响点。
第二次修正
> fit2 <- lm(weight ~ height + I(height^2), data=women)
Warning message:
显示串列没有完全被刷新
> par(mfrow=c(2,2))
> plot(fit2)
> #这儿的显示基本还算理想,但是观测点13和观测点15对整个回归的影响还是比较大,删除之后再看结果
> newfit<- lm(weight ~ height +I(height^2),data=women[-c(13,15),])
> par(mfrow=c(2,2))
Warning message:
显示串列没有完全被刷新
> plot(newfit)
继续来看运用函数进行修正
car包提供了大量函数,大大增强了拟合和评价回归模型的能力
qqPlot() 分位数比较图
durbinWatsonTest() 对误差自相关性做durbin-Watson检验
ncvTest() 对非恒定的误差方法做的分检验
speardLevelPlot() 分散水平检验
outlierTest() bonferronni离群点检验
avluencePlot() 回归影响图
scatterplot() 增强的散点图
scatterplotMatrix() 增强的散点图矩阵
vif() 方差膨胀因子
举例来说
> states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
> par(mfrow=c(2,2))
> plot(fit)
很明显,结果中“Nevada”是对结果的影响就比较大,属于噪点
可视化误差:
> states["Nevada",]
Murder Population Illiteracy Income Frost
Nevada 11.5 590 0.5 5149 188
> fitted(fit)["Nevada"] #显示拟合值
Nevada
3.878958
> residuals(fit)["Nevada"] #残差拟合值
Nevada
7.621042
> rstudent(fit)["Nevada"]
Nevada
3.542929
> #可见,Nevada有一个很大的正残差值(真实值-预测值),表明该模型低估了该州的谋杀率。Nevada的谋杀率是11.5%,而模型预测的谋杀率是3.9%。
绘制学生化残差图函数
> residplot<- function(fit, nbreaks=10){
+ z<- rstudent(fit)
+ hist(z, breaks=nbreaks,fre=FALSE, xlab="Studentized Residual", main="Distribution of Errors")
+ rug(jitter(z), col="brown")
+ curve(dnorm(x,mean=mean(z),sd=sd(z)), add=TRUE, col="blue", lwd=2)
+ lines(density(z)$x, density(z)$y,col="red", lwd=2, Ity=2)
+ legend("topright", legend=c("Normal Curve","Kernel Density Curve"), Ity=1:2, col=c("blue","red"), cex=.7)
+ }
> residplot(fit)
结果如下:
线性模型假设的综合验证
gvlma( )函数由pena和slate编写,能对线性模型假设进行综合验证,同时还能做偏斜度、峰度和差异方差性的评价。
> library(gvlma)
> gvmodel<- gvlma(fit)
> summary(gvmodel)
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level of Significance = 0.05
Call:
gvlma(x = fit)
Value p-value Decision
Global Stat 2.7728 0.5965 Assumptions acceptable.
Skewness 1.5374 0.2150 Assumptions acceptable.
Kurtosis 0.6376 0.4246 Assumptions acceptable.
Link Function 0.1154 0.7341 Assumptions acceptable.
Heteroscedasticity 0.4824 0.4873 Assumptions acceptable.
> #该结果中的P=0.597,高于显著性水平,因此接受原假设。
R语言回归诊断的基本知识到这就结束了,咱们下期再见!O(∩_∩)O哈哈~