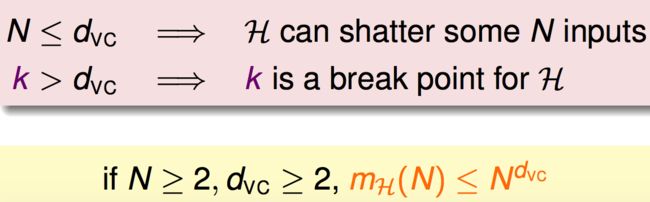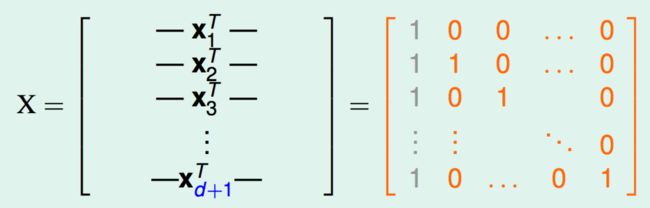VC dimension and Model complexity
可以把growth function m_H(N)的upper bound用N^(k-1)来限制, for N large, k>=3 Thus,
定义: VC Dimension: maximum non-break point 如果break point = k, then VC dimension = k-1 在VC Dimension上,这个Hset可以shatter某N个点,不一定是所有的N个点,但是如果N超过了VC dimension,则出现了Hset不能shatter掉的情况。 d_vc = minimun k -1
如果有另外一个N的input,可以被shatter,则d_vc>N。如果其他任何的N input都不能被shatter的话,则d_vc
1. if linear separable dataset, PLA can converge. After T(large) correction, Ein(g)=0 2. with x_n ~ P and y_n=f(x_n), the prob of (Ein(g)-Eout(g)>epislon) <= 4m_H(2N)exp(-1/8 * epislon^2 * N) (Hoeffding) if d_vc is finite. Then if N large, Eout(g) = Ein(g) PAC Combine with 1 and 2, Eout(g) = 0
Multiple feature d-D perceptrons: d_vc = d+1 证明: 先证d_vc >= d+1 (There are some d+1 inputs that can shatter) 输入d+1个点,每个点的维度为d再加上x_0=1,也就是那个threshold,一共是d+1维。把这d+1个维度为d+1的点写成矩阵形式:
第1个点全0,第2个点在第一个维度有1的分量,其他维度为0,第3个点在第二个维度有1的分量,其他维度为0,其他以此类推。然后最左边灰色的column就是那个threshold,就是x_0。这个矩阵是(d+1)*(d+1)维的,是可逆的,invertible。 对于任何一个dichotomy, 用y=[y_1, y_2,…,y_d+1]表示的话,可以有一个w,这个w也就是一个h在每个feature上的权重,通过这个h对d+1个点的Data进行划分,得到的其中一种dichotomy。那么现在对于任何一种dichotomy,都可以找到对应的w,即
所以对于这种特定的X,发现它可以被shatter,满足条件 (There are some d+1 inputs that can shatter),因此d_vc>=d+1 现在证d_vc<=d+1(任何>d+1,姑且就用d+2个点作为例子,都不能被shatter) 对于2D perceptron情况,对于输入是3个点而言,存在可以被shatter的3点input。在此基础上,加上一个点,变成了4点input。现在可否被shatter呢?假设原来三个点分别是+1,+1,-1,如果是这样的话,第4个点就无法是-1,原因是第四个点与前3个点有linear dependence,这restrict了dichotomy的种类。
因此对于2D情况,当输入的点的个数大于d+1,这里是d+2,都不可以被shatter。 对于一般的d维perceptron,每个点的维度是d+1维,现在输入d+2个点,把这些点用矩阵形式表示,
可以看到,第d+2个点x_d+2 可以由前d+1个点用线性表示,这是线代里面知识。 现在有个h,它的w满足
就是它满足对每个点x的划分的符号都与前面的a相同,那么这样产生出来的结果是正的,因此第d+2个点就不能被h划分为-1,此时说明如果有d+2个点作为input,这种情况是不可以被shatter的。因此d_vc<=d+1。 证毕。
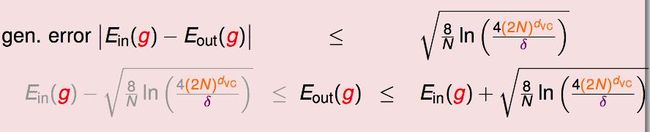
VC bound: 不等式右边,定义为delta,Bad发生的概率delta很小
相反,Good发生的概率,即P(|Ein(g)-Eout(g)|<=epislon) >= 1-delta
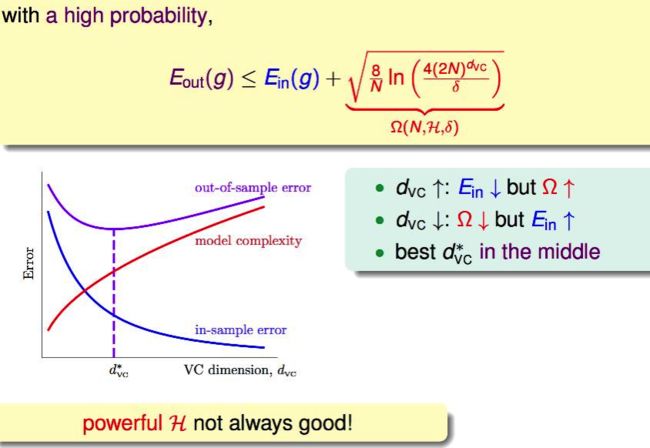
这个不等式,Ein和Eout有很大的概率,会被限制在根号那一项内,定义为Omega,就是model(Hset) complexity。
可以看到,随着VC dimension的上升,Hset就越来越powerful,Ein就会下降,但是这伴随着Model Complexity的penalty。某个时刻,Model Complexity 德penalty上升的量超过Ein下降的量,这样会导致Eout不降反升。 Sample Complexity:N 还是对于Hoeffding中的VC Bound delta
在外面有一个N,在exp中有一个N,外面的N和里面的N对delta的贡献分别是正和负的。 E.g:
一开始N=100or1000的时候,外面的N dominant,再增大以后,exp里的N开始dominant。从理论上来说,N需要的个数是d_vcd的10000倍,但是实际上只需要10倍。 这样的差距,说明我们计算的这个VC bound还是很宽松的,来源是
1. 不需要知道P和f 2. 没有用真正的dichotomy set的大小,而是用了成长函数(max dichotomy set),确保可以使用任何的Data,而不是某一特定的Data 3. 用成长函数的上限,也就是Dichotomy set上限的上限 4. 最差情况