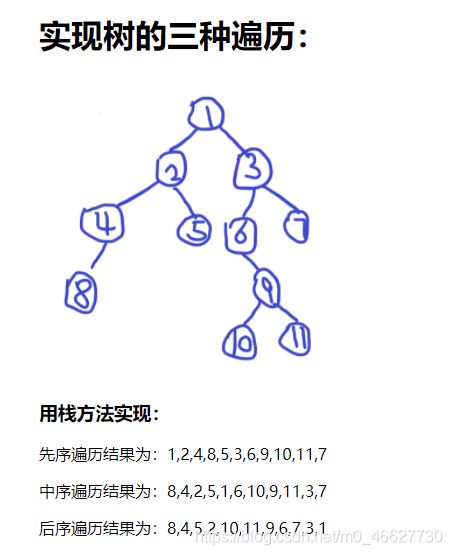
用栈实现树的三种遍历
这里写目录标题
-
- 前言
- 前期准备
- 先序遍历
- 后序遍历
- 中序遍历(个人埋头写出来的,没想到力扣上超时了,尴尬)
- 参照力扣官方给出来的中序遍历
- 结果图
前言
二叉树三种遍历的算法,可谓是程序员必须会的一个算法。最近在练习算法也对此研究了一段时间,通过递归,我们其实不难实现三种遍历方式,但通过栈来实现,感觉还是有点意思的。
其中在写中序遍历时发现了要是该树不是二叉树时有点错误,只好不断一遍遍检查思路,所以捣鼓了挺长时间的,真的有点艰辛,归根到底还是自己太菜了。
前期准备
var trees = {
value: 1,
left: {
value: 2,
left: {
value: 4,
left: {
value: 8,
left: null,
right: null
},
right: null
},
right: {
value: 5,
left: null,
right: null
}
},
right: {
value: 3,
left: {
value: 6,
left: null,
right: {
value: 9,
left: {
value: 10,
left: null,
right: null
},
right: {
value: 11,
left: null,
right: null
}
}
},
right: {
value: 7,
left: null,
right: null
}
}
}
先序遍历
思路:由于栈有先进后出的特点,而先序遍历又是:头节点 -> 左节点 -> 右节点 的顺序。所以先压入头结点,然后压入右节点,最后压入左节点,这样就可以实现弹栈的时候是先左节点后右节点了。
function pre() {
let result = '' // 结果排序
let stack = [] // 声明栈
let head = trees // 声明头结点为树头
stack.push(head) // 将头节点压入栈
// 栈不为空
while (stack.length) {
head = stack.pop() // 头结点为弹出节点
result += head.value + ',' // 输出该节点值
// 有右子树先压入右子树
if (head.right) {
stack.push(head.right)
}
// 然后才判断有左子树压入左子树
if (head.left) {
stack.push(head.left)
}
}
// 这里我是将结果插入到元素中显示,你们亦可以直接打印
document.getElementById('stack-pre').innerText = '先序遍历结果为:' + result.slice(0, result.length - 1)
}
后序遍历
思路:后序遍历是:左节点 -> 右节点 -> 头节点的顺序。所以先压入头结点,然后压入左节点,最后压入右节点,这样就可以实现弹栈的时候可以得到 头节点 -> 右节点 -> 左节点的顺序,然后再倒过来即可实现 左节点 -> 右节点 -> 头节点的顺序。
function next() {
let result = '' // 结果排序
let stack = [] // 声明栈
let head = trees // 声明头结点
stack.push(head) // 将头节点压入栈
// 栈不为空
while (stack.length) {
head = stack.pop() // 头结点为弹出节点
result = head.value + ',' + result // 输出该节点值
// 有左子树先压入左子树
if (head.left) {
stack.push(head.left)
}
// 然后才判断有右子树压入右子树
if (head.right) {
stack.push(head.right)
}
}
// 这里我是将结果插入到元素中显示,你们亦可以直接打印
document.getElementById('stack-next').innerText = '后序遍历结果为:' + result.slice(0, result.length - 1)
}
中序遍历(个人埋头写出来的,没想到力扣上超时了,尴尬)
思路:中序遍历是:左节点 -> 头节点 -> 右节点的顺序。所以先压入头结点,然后压入所有层级的左节点,弹出栈顶节点时判断是否有右子树,有则压入右子树反之表明该节点及其子树已遍历完成。
function middle() {
let result = '' // 结果排序
let stack = [] // 声明栈
let head = trees // 声明头结点,指向树头节点
stack.push(head) // 将树头结点压入栈中
let addLeft = true // 是否可以添加左子树,当该头结点没有右子树但有左子树时,遍历右子树再返回该头结点时,证明是第二次到达头结点,所以不可以再添加该头结点的左子树
// 栈不为空
while (stack.length) {
// 存在还没遍历过的左子树,则将该左子树压入栈并将头结点指向该左子树
if (addLeft && head.left) {
stack.push(head.left)
head = head.left
} else {
// 不存在左子树或者已遍历过该节点的左子树时,需要弹出栈顶并让头结点指向它,并输入该节点的值
head = stack.pop()
result += head.value + ','
// 如果该节点存在右子树,则允许其继续遍历左子树,并将该右节点压入栈和改变头结点指向
if (head.right) {
addLeft = true
stack.push(head.right)
head = head.right
} else {
// 无右子树的情况,则表明该栈顶节点已遍历完所有子树,不允许再添加已遍历过的左子树入栈
addLeft = false
}
}
}
// 这里我是将结果插入到元素中显示,你们亦可以直接打印
document.getElementById('stack-middle').innerText = '中序遍历结果为:' + result.slice(0, result.length - 1)
}
参照力扣官方给出来的中序遍历
思路:具体思路与我上面的差不多,但它更精妙地是采用两次while,从而避免了上面出现的多次条件判断,大大节省了运算时间。
function middle() {
let result = '' // 结果排序
let stack = [] // 声明栈
let head = trees // 声明头结点,指向树头节点
// 栈不为空或者头节点不为空
while (head || stack.length) {
// 不断将左子树节点压入栈中
while (head) {
stack.push(head)
head = head.left
}
// 该节点不存在左子树的时候,则弹栈并将head指向弹出节点的右节点,进而遍历其右子树
head = stack.pop()
result += head.value + ','
head = head.right
}
// 这里我是将结果插入到元素中显示,你们亦可以直接打印
document.getElementById('stack-middle').innerText = '中序遍历结果为:' + result.slice(0, result.length - 1)
}