Spark-MLlib协同过滤算法

协同过滤

协同过滤概述

协同过滤算法是一种基于群体用户或者物品的典型推荐算法，也是目前常用的推荐算法中最常用和最经典的算法。协同过滤算法的确认就是标准推荐算法作为一种可行的机器推荐算法标准步入正规。

基于用户的推荐

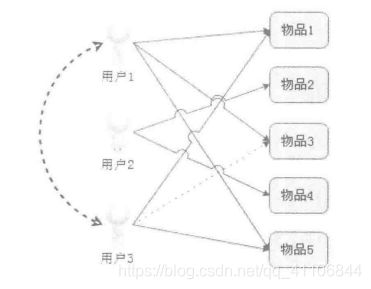
基于用户推荐的过滤算法可以理解为：用户1喜欢物品1，物品3，物品5；用户3喜欢物品1，物品5。从图上可以看出，用户1和用户2选择上的偏好更相似，所以给用户3推荐物品3是合理的。

基于物品的推荐

基于物品推荐的过滤算法可以理解为：用户3喜欢物品1和物品5，物品3和物品1是有相同标签的物品，所以用户3也会喜欢物品3。

协同过滤算法的不足

在实际应用中，基于用户的和基于物品的推荐算法均是最常用的协同过滤推荐算法。但是在某些场合下仍然具有不足之处。

首先是基于用户的推荐算法，针对某些热点物品的处理不够准确，对于一些常用的物品推荐，其计算结果往往排在推荐的首位，而这样的推荐却没有实际应用意义。同时基于用户的推荐算法，往往数据量较为庞大，计算费事，由于热点的存在准确度也很成问题。

基于物品的推荐算法相对于基于用户的推荐算法，其数据量小很多，可以较为容易地生成推荐值，但是其存在推荐同样（同类型）物品的问题。例如，用户购买了某件商品，那么推荐系统可能会继续推荐相同类型的商品给用户，用户在购买一件商品后绝对不会再购买同类型的商品，这样的推荐完全是失败的。

相似度度量

基于欧几里得距离的相似度计算

$$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

几里得相似度计算是一种基于用户之间直线距离的计算方式。在相似度计算中，不同的物品或者用户可以将其定义为不同的坐标点，而特定目标定位为坐标原点。

知道了两个坐标之间的直线距离，欧几里得相似度也就很好计算了，与d成反比，即其相似度公式如下：
$$s=\frac{1}{1+d}$$

基于余弦角度的相似度计算

与欧几里得距离相类似，余弦相似度也将特定目标，即物品或者用户作为坐标上的点，但不是坐标原点。基于此与特定的被计算目标进行夹角计算。
$$cos@=\frac{\sum (x_i\ast y_i)}{\sqrt{\sum (x_i^2)\ast \sum (y_i^2)}}$$
代码：

import org.apache.spark.{
     SparkConf, SparkContext}
import scala.collection.mutable.Map


object CollaborativeFilteringSpark {
     
    val conf = new SparkConf().setMaster("local").setAppName("CollaborativeFilteringSpark ")    //设置环境变量
    val sc = new SparkContext(conf)                                 //实例化环境
    val users = sc.parallelize(Array("aaa","bbb","ccc","ddd","eee"))       //设置用户
    val films = sc.parallelize(Array("smzdm","ylxb","znh","nhsc","fcwr"))    //设置电影名

    val source = Map[String,Map[String,Int]]()                //使用一个source嵌套map作为姓名电影名和分值的存储
    val filmSource = Map[String,Int]()                     //设置一个用以存放电影分的map
    def getSource(): Map[String,Map[String,Int]] = {
                 //设置电影评分
        val user1FilmSource = Map("smzdm" -> 2,"ylxb" -> 3,"znh" -> 1,"nhsc" -> 0,"fcwr" -> 1)
        val user2FilmSource = Map("smzdm" -> 1,"ylxb" -> 2,"znh" -> 2,"nhsc" -> 1,"fcwr" -> 4)
        val user3FilmSource = Map("smzdm" -> 2,"ylxb" -> 1,"znh" -> 0,"nhsc" -> 1,"fcwr" -> 4)
        val user4FilmSource = Map("smzdm" -> 3,"ylxb" -> 2,"znh" -> 0,"nhsc" -> 5,"fcwr" -> 3)
        val user5FilmSource = Map("smzdm" -> 5,"ylxb" -> 3,"znh" -> 1,"nhsc" -> 1,"fcwr" -> 2)
        source += ("aaa" -> user1FilmSource)                //对人名进行存储
        source += ("bbb" -> user2FilmSource)                 //对人名进行存储
        source += ("ccc" -> user3FilmSource)                 //对人名进行存储
        source += ("ddd" -> user4FilmSource)                 //对人名进行存储
        source += ("eee" -> user5FilmSource)                 //对人名进行存储
        source                                        //返回嵌套map
    }

    //两两计算分值,采用余弦相似性
    def getCollaborateSource(user1:String,user2:String):Double = {
     
        val user1FilmSource = source.get(user1).get.values.toVector        //获得第1个用户的评分
        val user2FilmSource = source.get(user2).get.values.toVector        //获得第2个用户的评分
        val member = user1FilmSource.zip(user2FilmSource).map(d => d._1 * d._2).reduce(_ + _).toDouble            //对公式分子部分进行计算
        val temp1  = math.sqrt(user1FilmSource.map(num => {
                 //求出分母第1个变量值
            math.pow(num,2)                                        //数学计算
        }).reduce(_ + _))                                        //进行叠加
        val temp2  = math.sqrt(user2FilmSource.map(num => {
                 求出分母第2个变量值
            math.pow(num,2)                                     //数学计算
        }).reduce(_ + _))                                        //进行叠加
        val denominator = temp1 * temp2                            //求出分母
        member / denominator                                    //进行计算
    }

    def main(args: Array[String]) {
     
        getSource()                                            //初始化分数
        val name = "bbb"                                        //设定目标对象
        users.foreach(user =>{
                                         //迭代进行计算
            println(name + " 相对于 " + user +"的相似性分数是："+ getCollaborateSource(name,user))
        })
    }
}
---------
bbb 相对于 aaa的相似性分数是：0.7089175569585667
bbb 相对于 bbb的相似性分数是：1.0000000000000002
bbb 相对于 ccc的相似性分数是：0.8780541105074453
bbb 相对于 ddd的相似性分数是：0.6865554812287477
bbb 相对于 eee的相似性分数是：0.6821910402406466

最小二乘法

最小二乘法（LS算法）是一种数学优化技术，他通过最小化误差的平方和寻求数据的最佳函数匹配。利用最小二乘法可以简便的求得未知的数据，并使得这些求得的数据与实际数据之间的误差的平方和最小。最小二乘法还可以用于曲线拟合。

从图中可以看到，若干个点依次分布在向量空间中，如果希望找到一条直线和这些点达到最佳匹配。那么最简单的方式就是希望这些点到直线的距离最小：
$$f(x)=ax+b^2$$

交替最小二乘法