王道考研2021——数据结构学习笔记
王道给的代码中,有些用的是c++,但是和c的区别不大,不影响理解。
ElemType e 指e为任意数据类型,如struct,int…
文章目录
- 线性表
-
- 顺序表
-
- 定义
-
- 静态分配
- 动态分配
- 初始化与增加动态数组长度
- 顺序表插入
- 顺序表删除
- 按位查找
- 按值查找
- 结构类型的比较
- 单链表
-
- 初始化
- 判断是否为空
- 按位查找
- 按值查找
- 求表长度
- 单链表插入
- 按位序删除
- 指定结点删除
- 尾插法建立单链表
- 头插法建立单链表
- 双链表
-
- 初始化
- 双链表插入
- 双链表删除
- 双链表遍历
- 循环链表
-
- 循环单链表
- 循环双链表
- *静态链表
-
- 定义
- 基本操作
- 栈
-
- 顺序栈的定义
- 初始化操作
- 判断栈空
- 进栈
- 出栈
- 读取栈顶元素
- *共享栈
- 链栈的定义
- 栈在括号匹配中的应用
- 栈在表达式求值中的应用
-
- 计算逆波兰表达式
- 队列
-
- 定义与初始化
- 判空
- 入队与判满
- 出队
- 获取队头元素值
- 队列节约空间的定义方式
- 链式队列
-
- 定义
- 初始化
- 判空
- 入队
- 出队
- *双端队列
- 特殊矩阵的压缩存储
- 串
-
- 定义
- 串的链式存储
- 求子串
- 比较
- 定位
- 朴素模式匹配算法
- KMP算法
- KMP算法的改进
- 树
-
- 概念
-
- 基本概念
- 结点关系描述
- 高度、深度、度
- 有序树和无序树
- 树和森林
- 树的常考性质
- 二叉树
-
- 概念
- 满二叉树和完全二叉树
- 二叉排序树
- 平衡二叉树
- 常考性质
- 顺序存储定义和初始化
- 顺序存储基本操作与判断
- 链式存储定义/初始化/插入
- 链式存储递归遍历
-
- 求树的深度(应用)
线性表
顺序表
定义
静态分配
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int length;
}SqList;
动态分配
#define InitSize 10 //默认的最大长度
typedef struct{
int *data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList;
初始化与增加动态数组长度
//用动态分配定义顺序表
void InitList(SeqList &L){
//用malloc函数申请一片连续的存储空间
L.data=(int *)malloc(InitSize*sizeof(int));
L.length=0; //设置长度容易忘
L.MaxSize=InitSize;
}
void IncreaseSize(SeqList &L,int len){
//先申请一个比之前大的空间,把原先的数组复制进去,再释放原先的空间
int *p=L.data;
L.data=(int *)malloc((L.MaxSize+len)*sizeof(int));
for(int i=0;i<L.length;i++){
L.data[i]=p[i]; //将数据复制到新区域
}
L.MaxSize=L.MaxSize+len; //顺序表最大长度增加len
free(p); //释放原先的内存空间
}
顺序表插入
此处后移,先移动靠后的元素,再移动靠前的元素
//用静态分配定义顺序表
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=L.MaxSize) //当前存储空间已满,不能插入
return false;
for(int j=L.length;j>=i;j--) //将第i个元素及之后的元素后移
L.data[j]=L.data[j-1];
L.data[i-1]=e; //在位置i处放入e
L.length++; //长度加1
return true;
}
顺序表删除
此处前移,先移动靠前的元素,再移动靠后的元素
//用静态分配定义顺序表
bool ListDelete(SqList &L,int i,int &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e=L.data[i-1]; //将被删除的元素赋值给e
for(int j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度减1
return true;
}
按位查找
由于随机访问,按位查找在顺序表中很容易实现
//用静态分配定义顺序表
ElemType GetElem(Sqlist L,int i){
return L.data[i-1];
}
按值查找
//用静态分配定义顺序表
int LocateElem(SeqList L,ElemType e){
for(int i=0;i<L.length;i++)
if(L.data[i]==e)
return i+1; //数组下表为i的元素值等于e,返回其位序i+1
return 0; //退出循环,说明查找失败
}
结构类型的比较
基本数据类型可以直接用==比较
//方法一,依次对比各个分量来判断两个结构体是否相等
if(a.num == b.num && a.people == b.people){
printf("相等");
}else{
printf("不相等");
}
//方法二,定义一个函数
bool isCustomerEqual(Customer a, Customer b){
if(a.num == b.num && a.people == b.people)
return true;
else
return false;
}
单链表
目前,只记了带头结点的情况
初始化
typedef struct LNode{
//定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
//LNode *和LinkList的意思是一样的,前者侧重结点,后者侧重链表
//初始化一个单链表
bool InitList(LinkList &L){
//&表示间接访问,和c语言使用二级指针同理
L=(LNode *)malloc(sizeof(LNode); //分配一个头结点
if(L==NULL) return false; //内存不足,分配失败
L->next=NULL; //头结点之后暂时还没有节点,赋值为NULL是好习惯
return true;
}
判断是否为空
bool Empty(LinkList L){
if(L->next==NULL) return true;
else return false;
}
按位查找
//按位查找,返回第i个元素
LNode *GetElem(LinkList L,int i){
if(i<0) return NULL;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p=L; //L指向头结点,头结点是第0个结点(不存数据)
while(p!=NULL && j<i){
p=p->next;
j++;
}
return p;
}
按值查找
LNode *LocateElem(LinkList L,ElemType e){
LNode *p = L->next;
//从第1个结点开始查找数据域为e的结点
while(p!=NULL && p->data !=e)
p=p->next;
return p; //找到后返回该结点指针,否则返回NULL
}
求表长度
//求表的长度
int Length(LinkList L){
//此处不需要间接访问
int len = 0; //统计表长
LNode *p = L;
while(p->next!=NULL){
p=p->next;
len++;
}
return len;
单链表插入
综合了 按位序+在指定结点后前/后插 的代码
//在第i个位置插入元素e
bool ListInsert(LinkList &L,int i,ElemType e){
if(i<1) return false;
//下面这一段可以用 LNode *p = GetElem(L,i-1); 代替,GetElem即为上方的按位查找函数
//可以把自己写出的函数存在一个文件中,直接引入即可
/***********************************************************************/
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点,头结点是第0个结点(不存数据)
while(p!=NULL && j<i-1){
//循环找到第i-1个结点
p=p->next;
j++;
}
/***********************************************************************/
return InsertNextNode(p,e); //封装的好处
//return InsertPrevNode(p,e);
}
//后插操作:在p结点之后插入元素e
bool InsertNextNode(LNode *p,ElemType e){
if(p==NULL) return false;
//这个函数将会在其他函数中调用,p可能指向NULL,这样写可以使算法更健壮
LNode *s = (LNode *)malloc(sizeof(LNode));
if(s==NULL) return false; //内存分配失败
s->data = e; //用结点s保存数据元素e
//后插操作
s->next=p->next;
p->next=s; //将结点s连到p之后
//拓展:前插操作
s->next=p->next; //修改指针域
p->next=s;
temp=p->data; //交换数据域部分
p->data=s->data;
s->data=temp;
return true;
}
按位序删除
bool ListDelete(LinkList &L,int i,ElemType &e){
if(i<1) return false;
//下面这一段可以用 LNode *p = GetElem(L,i-1); 代替,GetElem即为上方的按位查找函数
/***********************************************************************/
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p=L; //L指向头结点,头结点是第0个结点(不存数据)
while(p!=NULL && j<i-1){
//循环找到第i-1个结点
p=p->next;
j++;
}
/***********************************************************************/
if(p==NULL) return false; //i值不合法
if(p->next == NULL) return false; //第i-1个结点之后已无其他结点
LNode *q=p->next; //令q指向被删除结点
e = q->data; //用e返回元素的值(不禁联系到js和python的pop方法)
p->next=q->next; //将*q结点从链中“断开”
free(q); //释放结点的存储空间
return true; //删除成功
}
指定结点删除
先用后继结点q的数据域覆盖当前结点p的数据域,然后把当前结点的指针域指向下下个结点,删掉q。
bool DeleteNode(LNode *p){
if(p==NULL) return false;
LNode *q=p->next; //令q指向*p的后继结点
p->data=q->data; //用后继结点的数据域覆盖自己的
p->next=q->next; //将*q结点从链中“断开”
free(q); //释放后继结点的存储空间
return true;
}
尾插法建立单链表
王道版:
typedef struct LNode{
//定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
LinkList List_TailInsert(LinkList &L){
//正向建立单链表
int x; //设ElemType为整型
L=(LinkList)malloc(sizeof(LNode)); //建立头结点
L->next=NULL; //初始为空链表
LNode *s,*r=L; //s总是指向最新生成的结点,r为表尾指针
scanf("%d",&x); //输入结点的值
while(x!=9999){
//输入9999表示结束
s=(LNode *)malloc(sizeof(LNode));
s->data=x;
r->next=s;
r=s; //r指向新的表尾结点
scanf("%d",&x);
}
r->next=NULL; //尾结点指针置空
return L;
}
学校版:
把数组内的数存入链表
#include 头插法建立单链表
这种方法可以将链表逆置,为常考点
思路:每个新的结点都插在头结点之后
LinkList HeadInsert(LinkList &L){
//逆向建立单链表
LNode *s;
int x;
L=(LinkList)malloc(sizeof(LNode)); //创建头结点
L->next=NULL; //初始为空链表
scanf("%d",&x); //输入结点的值
while(x!=9999){
//输入9999表示结束
s=(LNode *)malloc(sizeof(LNode)); //创建新结点
s->data=x;
s->next=L->next;
L->next=s; //将新结点插入表中,L为头指针
scanf("%d",&x);
}
return L;
}
双链表
初始化
typedef struct DNode{
ElemType data;
struct DNode *prior,*next;
}DNode,*DLinklist;
bool InitDLinkList(DLinklist &L){
L = (DNode *)malloc(sizeof(DNode)); //分配一个头结点
if(L==NULL) return false; //内存不足,分配失败
L->prior = NULL; //头结点的prior永远指向NULL
L->next = NULL; //头结点之后暂时还无结点
return true;
}
双链表插入
双链表的插入略微比单链表的插入复杂,要明白它插入的过程:
指定位置插入结点的代码(可以结合按位序):
bool InsertNextDNode(DNode *p,DNode *s){
if(p==NULL||s==NULL) return false; //非法参数
s->next=p->next;
if(p->next!==NULL) //如果p结点有后继节点
p->next->prior=s;
s->prior=p;//修改指针时要注意顺序
p->next=s;
}
双链表删除
//删除p结点的后继结点
bool DeleteNextDNode(DNode *p){
if(p==NULL) return false;
DNode *q=p->next; //找到p的后继结点q
if(q==NULL) return false; //p没有后继
p->next=q->next;
if(q->next!=NULL) //q结点不是最后一个结点
q->next->prior=p; //释放结点空间
free(q); //释放结点空间
return true;
}
//循环释放各个数据结点
void DestoryList(DLinklist &L){
while(L->next!=NULL)
DeleteNextDNode(L);
free(L); //释放头结点
L=NULL; //头指针指向NULL
}
双链表遍历
遍历的目的是对结点p做相应处理,如打印
//后向遍历
while(p!=NULL){
p=p->next;
}
//前向遍历
while(p!=NULL){
p=p->prior;
}
//前向遍历(跳过头结点)
while(p->prior!=NULL){
p=p->prior;
}
循环链表
循环单链表
在初始化时,头指针指向自己(普通单链表指向NULL)
L->next = L;

//判断结点p是否为循环单链表的表尾结点
bool isTail(LinkList L,LNode *p){
if(p->next==L) return true;
else return false;
}
//判断循环单链表是否为空
bool Empty(LinkList L){
if(L->next==L) return true;
else return false;
}

循环链表的好处:很多时候对链表的操作都是在头部或尾部,可以让L指向表尾元素,降低时间复杂度。(暂时没有这部分代码)
循环双链表
在初始化时,头结点的prior和next都指向自己。
L->prior = L;
L->next = L;

//判断结点p是否为循环双链表的表尾结点
bool isTail(DLinklist L,DNode *p){
if(p->next==L) return true;
else return false;
}
//判断循环双链表是否为空
bool Empty(DLinklist L){
if(L->next == L) return true;
else return false;
}

*静态链表
定义
静态链表由数据和游标构成,游标存储下一个结点的位置
#define MaxSize 10 //静态链表的最大长度
struct Node{
//静态链表结构类型的定义
ElemType data; //存储数据元素
int next; //下一个元素的数组下标
}SLinkList[MaxSize];
基本操作
此处不是很重要,代码不写也可以
初始化:
- 尾结点的next值赋值为-1
- 为避免内存脏数据污染,空结点的next先赋值为-2
查找:从头结点出发挨个往后遍历结点
插入位序为i的结点:
- 找到空结点,存入数据元素
- 从头结点出发找到位序为i-1的结点
- 修改新结点的next
- 修改i-1号结点的next
删除某个结点:
- 从头结点出发找到前驱节点
- 修改前驱节点的游标
- 被删除结点next设为-2
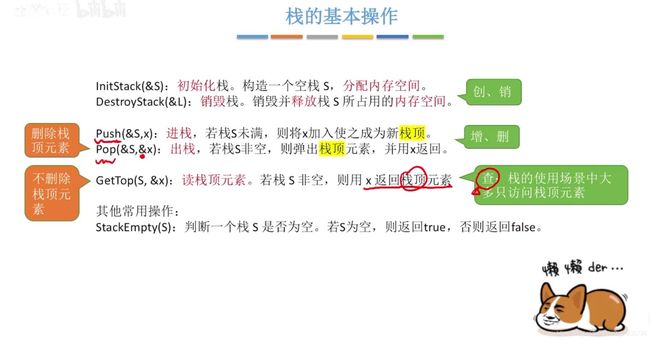
栈
逻辑上的出栈和清空栈只是改了栈顶指针(下标),由于没有用malloc申请空间,在声明栈的时候分配内存,在程序运行完毕后会自动回收内存,所以我们不用关心物理上的清空栈操作。
顺序栈的定义
栈由静态数组和栈顶指针组成,其中栈顶指针存放的是数组下标
此处讨论的都是 栈顶指针指向最上方元素 的情况,还有一种情况是 指针指向最上方元素上方一个位置 的情况,这两者在入栈和出栈时的自增自减符号位置有区别,判断栈满的条件也不同。
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶指针
}SqStack; //Sq:sequence——顺序
初始化操作
void InitStack(SqStack &S){
S.top=-1; //初始化栈顶指针
}
判断栈空
下面的几个操作中,可以把判断栈空的语句用这个函数替换
bool StackEmpty(SqStack S){
if(S.top == -1) return true; //空
else return false; //非空
}
进栈
bool Push(SqStack &S,ElemType x){
if(S.top==MaxSize-1) return false; //栈满,报错
S.top = S.top + 1; //指针先加1
S.data[S.top]=x; //新元素入栈
//可以写成S.data[++S.top]=x;
return true;
}
出栈
出栈和读取栈顶元素的区别是,出栈在逻辑上会删除栈顶的元素,而后者不会删除
bool Pop(SqStack &S,ElemType &x){
if(S.top == -1) return false; //栈空,报错
x=S.data[S.top]; //栈顶元素先出栈
S.top = S.top - 1; //指针再减1
//可以写成x=S.data[S.top--];
return true;
}
备注:出栈只是从逻辑上删除了栈顶元素(指针下移),但实际上数据还在内存中
读取栈顶元素
bool GetTop(SqStack S,ElemType &x){
if(S.top == -1) return false; //栈空,报错
x=S.data[S.top]; //x记录栈顶元素
return true;
}
*共享栈
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top0; //0号栈栈顶指针
int top1; //1号栈栈顶指针
}SqStack; //Sq:sequence——顺序
//初始化栈
void InitStack(ShStack &S){
S.top0=-1; //初始化栈顶指针
S.top1=MaxSize;
}
栈满的条件:top0 + 1 == top1
链栈的定义
这部分老师没有给出基本操作的代码,以后有空自己写一下,建立链栈和头插法建立链表是类似的。
typedef struct Linknode{
ElemType data; //数据域
struct Linknode *next; //指针域
}*LiStack //栈类型定义·
栈在括号匹配中的应用
算法实现:
建议基本操作再写一遍
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶指针
}SqStack; //Sq:sequence——顺序
bool bracketCheck(char str[],int length){
SqStack S;
InitStack(S); //初始化栈
for(int i=0;i<length;i++){
if(str[i]=='(' || str[i]=='[' || str[i]=='{'){
Push(S,str[i]); //扫描到左括号,入栈
}else{
if(StackEmpty(S)) return false;
//扫描到右括号,且此时栈空,匹配失败
char topElem;
Pop(S,topElem); //栈顶元素出栈
if(str[i]==')' && topElem!='(')
return false;
if(str[i]==']' && topElem!='[')
return false;
if(str[i]=='}' && topElem!='{')
return false;
}
}
return StackEmpty(S); //检索完全部括号后,栈空说明匹配成功
}
栈在表达式求值中的应用
计算逆波兰表达式
本关任务:
利用值栈对逆波兰表达式进行求值。逆波兰表达式从键盘输入,其中的运算符仅包含加、减、乘、除4种运算,表达式中的数都是十进制数,用换行符结束输入。由于逆波兰表达式的长度不限,所以值栈要用后进先出链表实现。
基本操作定义的方法和上方有出入,比如创建栈的函数有两种情况:
①不传参数,函数的作用就是把栈的结构返回
②传入指向栈的指针,用函数修改后,再把它带回来
(不知道为什么,educoder上可以正确运行,dev则错误)
#include 队列
定义与初始化
#define MaxSize 10 //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //用静态数组存放队列元素
int front,rear; //队头指针和队尾指针
//一般队头指向第一个元素,队尾指向最后一个元素的下一个位置
}SqQueue;
void InitQueue(SqQueue &Q){
//初始时队头、队尾指针指向0
Q.rear=Q.front=0;
}
计算队列元素个数:(rear+MaxSize-front)%MaxSize
判空
当队头和队尾指向同一个元素时,则队空
bool QueueEmpty(SqQueue Q){
if(Q.rear==q.front) return true; //队空条件
else return false;
}
入队与判满
判满需要用循环队列(利用取模运算)实现,用模运算将存储空间在逻辑上变成了环状
当队尾的上一个元素为队头时,则队满

bool EnQueue(SqQueue &Q,ElemType x){
if((Q.rear+1)%MaxSize==Q.front)
return false; //队满则报错
Q.data[Q.rear]=x; //新元素插入队尾
Q.rear=(Q.rear+1)%MaxSize; //队尾指针加1取模
return true;
}
出队
删除一个队头元素,并用x返回
bool DeQueue(SqQueue &Q,ElemType &x){
if(Q.rear==Q.front) return false; //队空则报错
x=Q.data[Q.front];
Q.front=(Q.front+1)%MaxSize; //队头指针后移
return true;
}
获取队头元素值
bool GetHead(SqQueue Q,ElemType &x){
if(Q.rear==Q.front) return false; //队空则报错
x=Q.data[Q.front];
//和出队相比,不改变队头指针
return true;
}
队列节约空间的定义方式
由于按照上方的定义方式,队满的条件是:队尾的上一个元素是队头,而队尾又指向最后一个元素的上一个位置,所以会导致一个位置大小空间的浪费,有如下改进方案(这些针对考研题目,只需记住上方的即可)
//size
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int front,rear;
int size; //队列当前长度
//初始化时rear=front=0;size=0;
//插入成功size++;删除成功size--;
//队满条件:size==MaxSize;
}SqQueue;
为了不浪费空间,把队头队尾指向同一个元素作为判断队空/队满的条件。但当发生这种情况时,可能队空也可能队满,tag用于判断最近进行的是删除还是插入。只有删除操作才可能导致队空,只有插入操作才可能导致队满。
每次删除成功时,令tag=0;插入成功时,令tag=1
//tag
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int front,rear;
int tag;
//初始化时,rear=front=0;tag=0;
//队空条件:front==rear && tag==0
//队满条件:front==rear && tag==1
}SqQueue;
链式队列
只研究带头结点的情况
定义
typedef struct LinkNode{
//链式队列结点
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{
//链式队列
LinkNode *front,*rear; //队列的队头和队尾指针
}LinkQueue;
初始化
void InitQueue(LinkQueue &Q){
//初始时,front、rear都指向头结点
Q.front=Q.rear=(LinkNode *)malloc(sizeof(LinkNode));
Q.front->next=NULL;
}
判空
bool IsEmpty(LinkQueue Q){
if(Q.front==Q.rear) return true;
//当队头指针和队尾指针指向同一个元素时,队列为空
else return false;
}
入队
void EnQueue(LinkQueue &Q,ElemType x){
LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));
s->data=x;
s->next=NULL;
Q.rear->next=s; //新结点插入到rear之后
Q.rear=s; //修改表尾指针
}
出队

bool DeQueue(LinkQueue &Q,ElemType &x){
if(Q.front==Q.rear) return false;
LinkNode *p=Q.front->next;
x=p->data; //用变量x返回队头元素
Q.front->next=p->next; //修改头结点的next指针
if(Q.rear==p) //如果此时是最后一个结点出队
Q.rear=Q.front; //修改rear指针
free(p); //释放结点空间
return true;
}
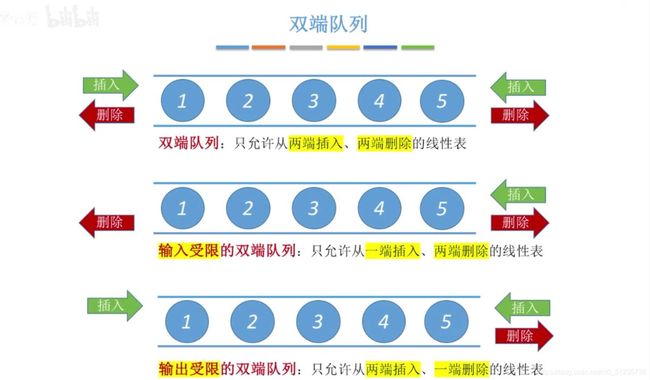
*双端队列
特殊矩阵的压缩存储
串
定义
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN]; //每个分量存储一个字符
int length; //串的实际长度
}SString;
串的链式存储
typedef struct StringNode{
char ch; //每个结点存1个字符
struct StringNode *next;
}StringNode,*String;
存储密度低
typedef struct StringNode{
char ch[4]; //每个结点存4个字符,还可以更多
struct StringNode *next;
}StringNode,*String;
求子串
SubString(&Sub,S,pos,len):求子串,用Sub返回串S的第pos个字符起长度为len的子串。
bool SubString(SString &Sub,SString S,int pos,int len){
if(pos+len-1 > S.length)
return false; //子串范围越界
for(int i=pos;i<pos+len;i++)
Sub.ch[i-pos+1] = S.ch[i];
Sub.length = len;
return true;
}
比较
StrCompare(S,T):比较操作。若S>T,则返回值>0;若S=T,则返回值=0;若S 该程序值得学习 Index(S,T):定位操作。若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置;否则函数值为0。 这个算法做的事,和上方的类似 以google为例,谈谈KMP算法存在的问题 改进: 树是一种递归定义的数据结构 定义 初始化 为了让这些操作在非完全二叉树中也有效,二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来 顺序存储的最坏情况:高度为h且只有h个结点的单支树(所有结点只有右孩子),也至少需要2^h -1个存储单元,浪费空间 又叫二叉链表: 用这种方式,很容易找到值定结点的左孩子或右孩子,但找它的父节点,只能从根开始遍历寻找,对此,还可以在定义结构体的时候加上父结点指针(三叉链表),这样方便找父结点,但是不常考 遍历分为三种次序:先序、中序和后序,本质上是一样的 先序遍历(PreOrder)的操作过程: 对于中序和后序遍历,只需要将“访问根节点”放在第二步、第三步即可 和后序遍历很像(后序遍历的visit(T)在第三行)
int StrCompare(SString S,SString T){
for(int i=1;i<=S.length && i<=T.length;i++){
if(S.ch[i]!=T.ch[i])
return S.ch[i]-T.ch[i];
}
return S.length-T.length;
//扫描过的所有字符都相同,则长度长的串更大
}
定位
int Index(SString S,SString T){
int i=1,n=StrLength(S),m=StrLength(T);
//StrLength只需要返回串结构体中的length即可
SString sub; //用于暂存子串
while(i<=n-m+1){
SubString(sub,S,i,m);
if(StrCompare(sub,T)!=0) ++i;
else return i; //返回子串在主串中的位置
}
return 0; //S中不存在与T相等的子串
}
朴素模式匹配算法
int Index(SString S,SString T){
int k=1;
int i=k,j=1;
while(i<=S.length && j<=T.length){
if(S.ch[i]==T.ch[j]){
++i;
++j; //继续比较后继字符
}else{
k++; //检查下一个子串
i=k;
j=1;
}
}
if(j>T.length) return k;
else return 0; //j<=T.length,说明最后主串长度不够了,匹配失败
}
int Index(SString S,SString T){
int i=k,j=1;
while(i<=S.length && j<=T.length){
if(S.ch[i]==T.ch[j]){
++i;
++j; //继续比较后继字符
}else{
i=i-j+2;
j=1; //指针后退重新开始匹配
}
}
if(j>T.length) return i-T.length;
else return 0; //j<=T.length,说明最后主串长度不够了,匹配失败
}
KMP算法
//求得的next值,等于最大相等前后缀长度+1
//前缀和后缀,都只是算j以及j之前的字符,比如google,如果j=4,指向第二个g,那么前缀有{g,go,goo},后缀有{g,og,oog},最大相等前后缀长度为1
void get_next(SString T,int next[]){
int i=1, j=0;
next[1]=0;
while(i<T.length){
if(j==0||T.ch[i]==T.ch[j]){
++i;++j;
//若pi=pj,则next[j+1]=next[j]+1
next[i]=j;
}
else
//否则令j=next[j],循环继续
j=next[j];
}
}
int Index_KMP(SString S,SString T){
int i=1,j=1;
int next[T.length+1];
//第0位不存数据,所以总长度+1
get_next(T,next); //求模式串的next数组
while(i<=S.length&&j<=T.length){
if(j==0||S.ch[i]==T.ch[j]){
++i;
++j; //继续比较后续字符
}
else
j=next[j]; //模式串向右移动
}
if(j>T.length)
return i-T.length; //匹配成功
else
return 0;
}
KMP算法的改进

现在第四个字符是g,不匹配,根据next数组,j指向1,而第一个字符是也是g,j又指向0,紧接着j++和i++…显然这里多走了一次,应该让j直接指向0。
先算出next数组int nextval[T.length+1];
nextval[1]=0;
for(int j=2;j<=T.length;j++){
if(T.ch[next[j]]==T.ch[j])
nextval[j]=nextval[next[j]];
//如果满足next[j]号字符和j号字符相同,用之前的next值覆盖之后的next值
//比如google的第四个g和第一个g相同,
//就把第一个g对应的next值(0)赋给第四个g对应的next值
else nextval[j]=next[j];
//否则就还和next的值一样
}
树
概念
基本概念
结点关系描述

如果使用了“堂兄弟结点”这个词,是想强调两个结点在同一层(一般不常用)高度、深度、度
有序树和无序树
树和森林
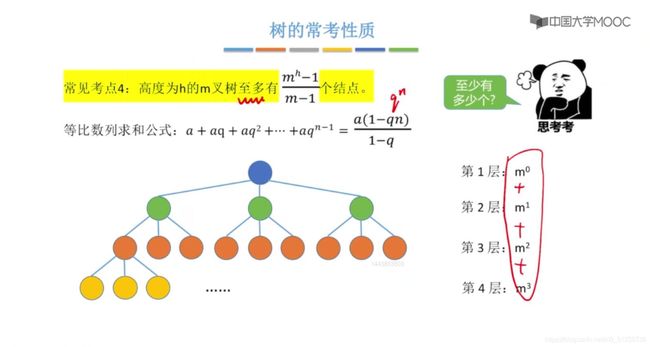
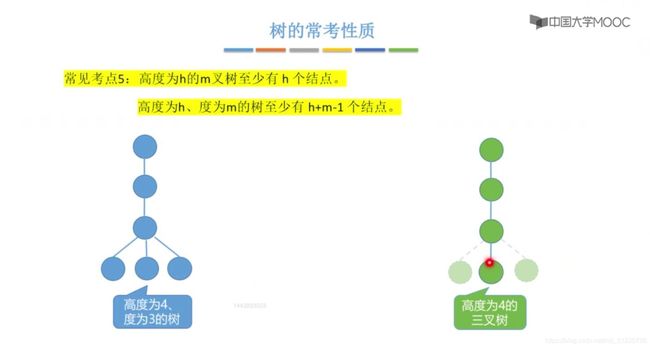
树的常考性质
二叉树
概念
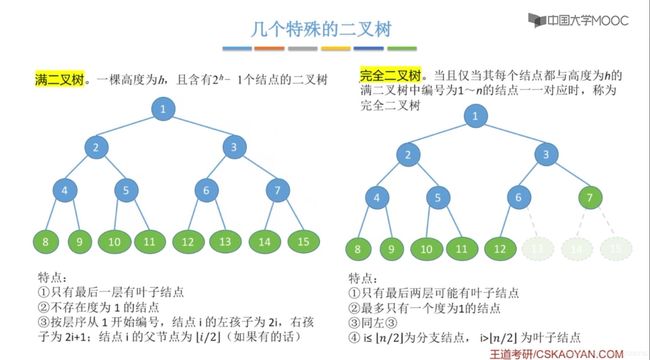
满二叉树和完全二叉树
二叉排序树
平衡二叉树
常考性质
顺序存储定义和初始化
#define MaxSize 100
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
};
TreeNode t[MaxSize];
//定义一个长度为MaxSize的数组t,按照从上至下、从左至右的顺序依次存储完全二叉树中的各个结点
for(int i=0;i<MaxSize;i++){
t[i].isEmpty=true;
//初始化时所有结点标记为空
}
顺序存储基本操作与判断

结论:二叉树的顺序存储结构,只适合存储完全二叉树链式存储定义/初始化/插入

typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//定义一棵空树
BiTree root = NULL;
//插入根节点
root = (BiTree)malloc(sizeof(BiTNode));
root->data = 1;
root->lchild = NULL;
root->rchild = NULL;
//插入新结点
BiTNode *p = (BiTNode *)malloc(sizeof(BiTNode));
p->data = 2;
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; //作为根节点的左孩子
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild,*rchild;
struct BiTNode *parent; //父结点指针
}
链式存储递归遍历
void PreOrder(BiTree T){
if(T!=NULL){
visit(T); //访问根节点(visit可以是任意操作,比如打印结点的值)
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
求树的深度(应用)
int treeDepth(BiTree T){
if(T == NULL){
return 0;
}
else{
int l = treeDepth(T->lchild);
int r = treeDepth(T->rchild);
//树的深度=Max(左子树深度,右子树深度)+1
return l>r? l+1:r+1;
}
}