YOLO v4常见的非线性激活函数详解

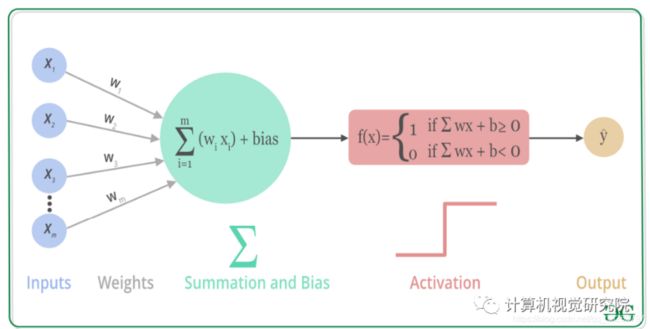
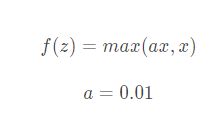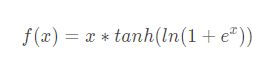YOLO v4中用到的激活函数是Mish激活函数
在YOLO v4中被提及的激活函数有: ReLU, Leaky ReLU, PReLU, ReLU6, SELU, Swish, Mish
其中Leaky ReLU, PReLU难以训练，ReLU6转为量化网络设计

激活函数使用过程图：

一、饱和激活函数

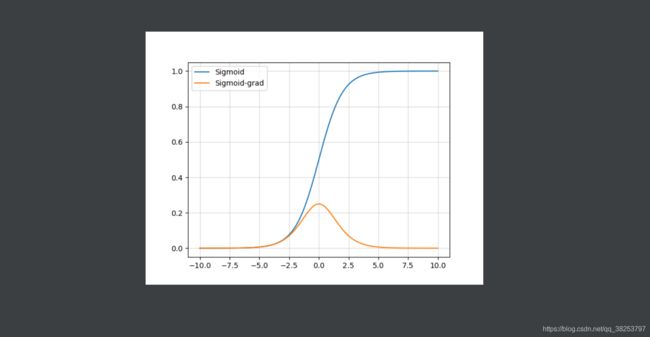
 1.1、Sigmoid

函数表达式：

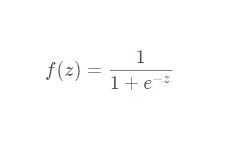
Sigmoid函数图像及其导数图像：

优点：

• 是一个便于求导的平滑函数；
• 能压缩数据，使输出保证在 [ 0 , 1 ] [0,1] [0,1]之间（相当于对输出做了归一化），保证数据幅度不会有问题；
• (有上下界)适合用于前向传播，但是不利于反向传播。

缺点：

• 容易出现梯度消失(gradient vanishing)，不利于权重更新；
• 不是0均值（zero-centered）的，这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。以 f=sigmoid(wx+b)为例， 假设输入均为正数（或负数），那么对w的导数总是正数（或负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。
• 指数运算，相对耗时。

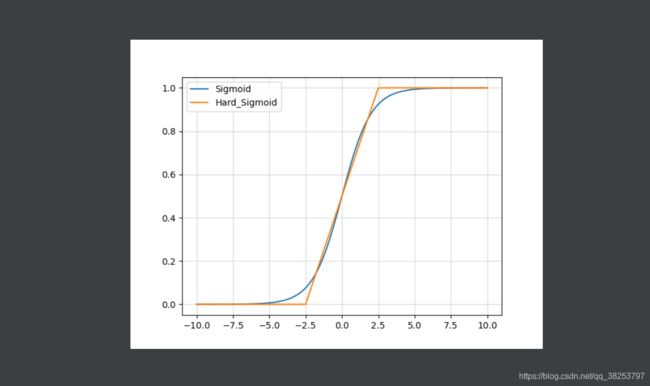
1.2、hard-Sigmoid函数

hard-Sigmoid函数时Sigmoid激活函数的分段线性近似。

函数公式：

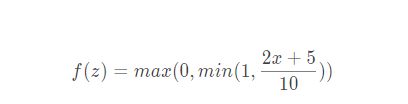
hard-Sigmoid函数图像和Sigmoid函数图像对比：

hard-Sigmoid函数图像及其导数图像：

优点：

1. 从公示和曲线上来看，其更易计算，没有指数运算，因此会提高训练的效率。

缺点：

1. 首次派生值为零可能会导致神经元died或者过慢的学习率。

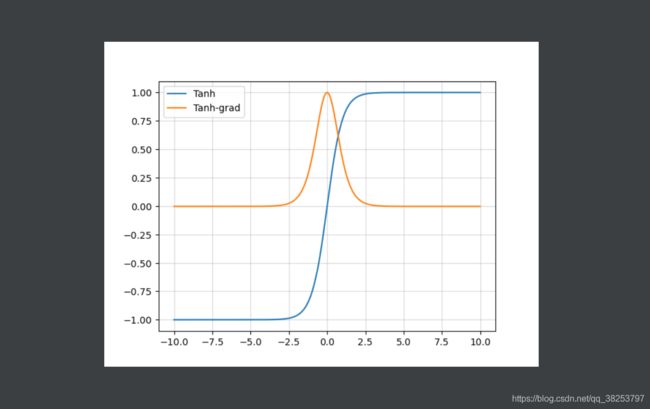
1.3、Tanh双曲正切

函数表达式：

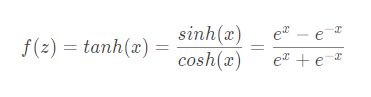
Tanh函数图像及其导函数图像:

优点：

1. 解决了Sigmoid函数的非zero-centered问题
2. 能压缩数据，使输出保证在 [ 0 , 1 ] [0,1] [0,1]之间（相当于对输出做了归一化），保证数据幅度不会有问题；(有上下界)

缺点:

• 还是容易出现梯度消失(gradient vanishing)，不利于权重更新；
• 指数运算，相对耗时。

二、非饱和激活函数

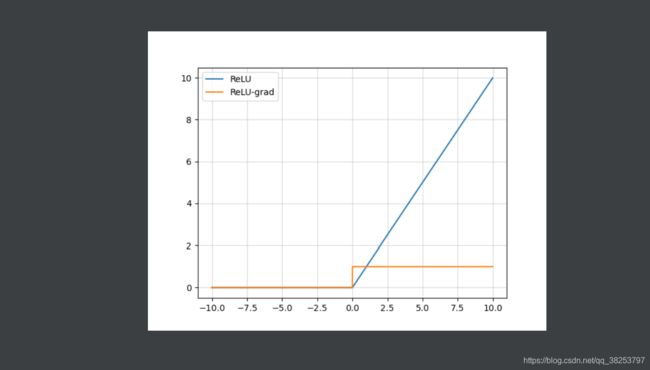
 2.1、ReLU(修正线性单元)

函数表达式：

f ( z ) = m a x ( 0 , x ) f(z)=max(0,x) f(z)=max(0,x)

ReLU函数图像及其导数图像：

优点:

1. ReLu的收敛速度比 sigmoid 和 tanh 快；
2. 输入为正时，解决了梯度消失的问题，适合用于反向传播。；
3. 计算复杂度低，不需要进行指数运算；

缺点:

• ReLU的输出不是zero-centered；
• ReLU不会对数据做幅度压缩，所以数据的幅度会随着模型层数的增加不断扩张。(有下界无上界)
• Dead ReLU Problem（神经元坏死现象）：x为负数时，梯度都是0，这些神经元可能永远不会被激活，导致相应参数永远不会被更新。（输入为负时，函数存在梯度消失的现象）

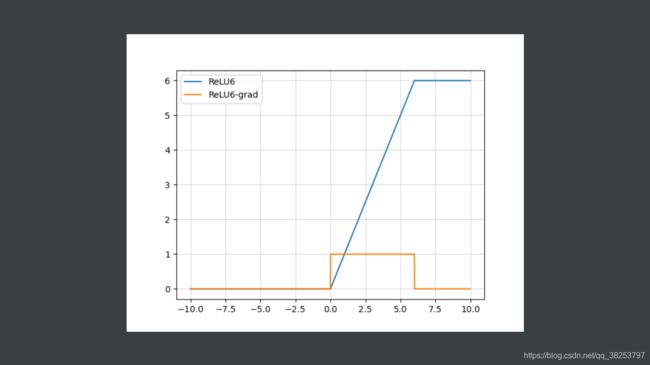
 2.2、ReLU6(抑制其最大值)

函数表达式：

ReLU函数图像和ReLU6函数图像对比：

ReLU6函数图像及其导数图像：

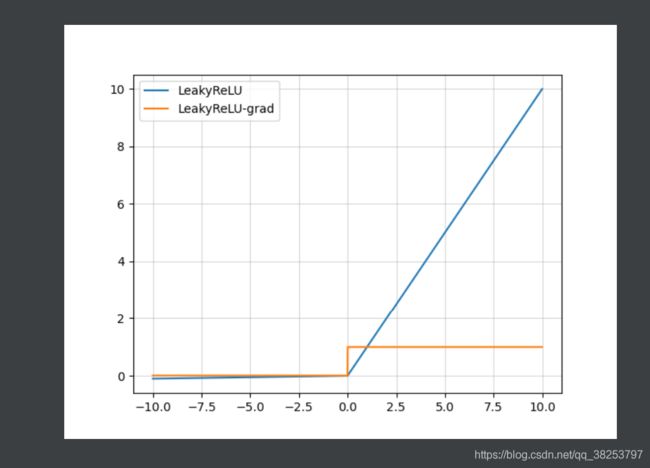
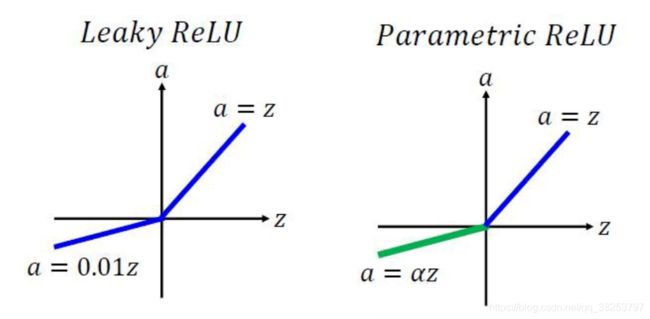
2.3、Leakly ReLU

函数表达式：

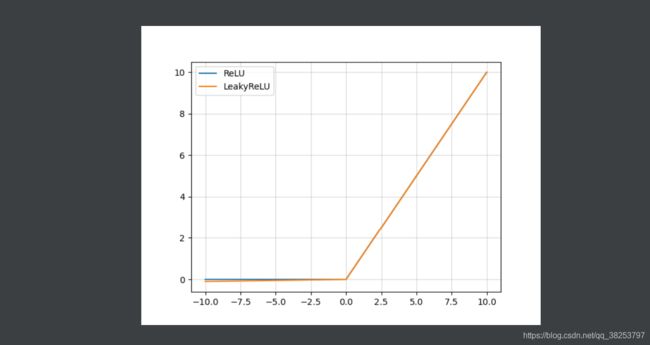
ReLU函数图像和Leakly ReLU函数图像对比：

Leakly ReLU函数图像及其导数图像：

优点：

1. 解决上述的dead ReLU现象， 让负数区域也会梯度消失；

理论上Leaky ReLU 是优于ReLU的，但是实际操作中，并不一定。

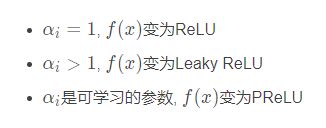
2.4、PReLU(parametric ReLU)

函数公式：

注意：

函数图像：

优点：

• 可以避免dead ReLU现象；
• 与ELU相比,输入为负数时不会出现梯度消失。

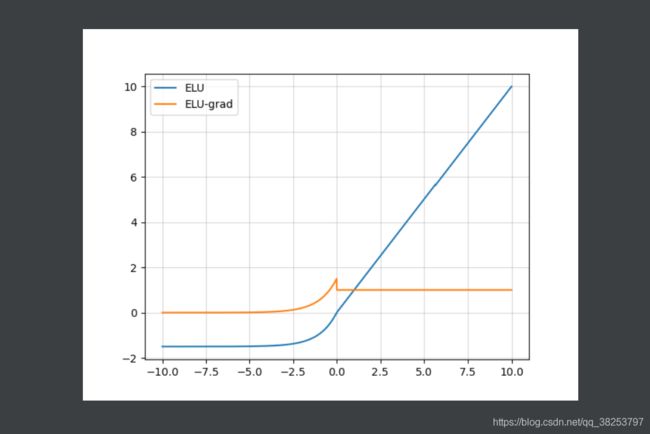
2.5、ELU(指数线性函数)

函数表达式：

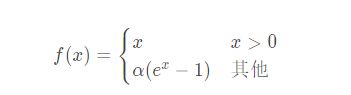
ELU函数图像及其导数图像（ α = 1.5 \alpha=1.5 α=1.5）：

优点：

• 有ReLU的所有优点，且没有Dead ReLU Problem（神经元坏死现象）；
• 输出是zero-centered的，输出平均值接近0；
• 通过减少偏置偏移的影响，使正常梯度更加接近自然梯度，从而使均值向0加速学习。

缺点：

• 计算量更高了。

理论上ELU优于ReLU, 但是真实数据下，并不一定。

2.6、SELU

SELU就是在ELU的基础上添加了一个 λ \lambda λ参数，且 λ > 1 \lambda>1 λ>1

函数表达式：

ELU函数图像和SELU函数图像对比( α = 1.5 , λ = 2 \alpha=1.5, \lambda=2 α=1.5,λ=2)：

SELU函数图像及其导数图像（ α = 1.5 , λ = 2 \alpha=1.5, \lambda=2 α=1.5,λ=2）：

优点：

1. 以前的ReLU、P-ReLU、ELU等激活函数都是在负半轴坡度平缓，这样在激活的方差过大时可以让梯度减小，防止了梯度爆炸，但是在正半轴其梯度简答的设置为了1。而SELU的正半轴大于1，在方差过小的时候可以让它增大，但是同时防止了梯度消失。这样激活函数就有了一个不动点，网络深了之后每一层的输出都是均值为0，方差为1. 2.7、Swish

函数表达式：

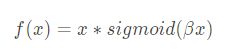
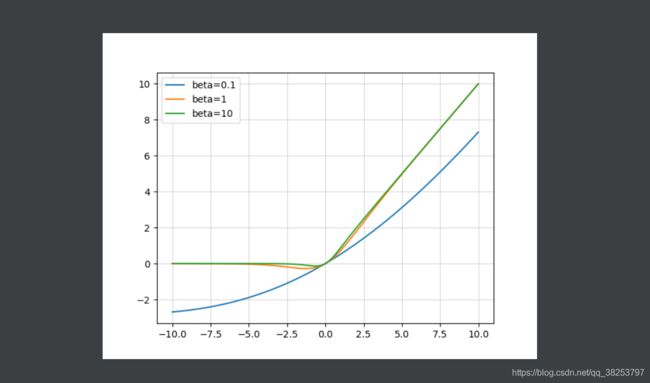
Swish函数图像( β = 0.1 , β = 1 , β = 10 \beta=0.1, \beta=1,\beta=10 β=0.1,β=1,β=10)：

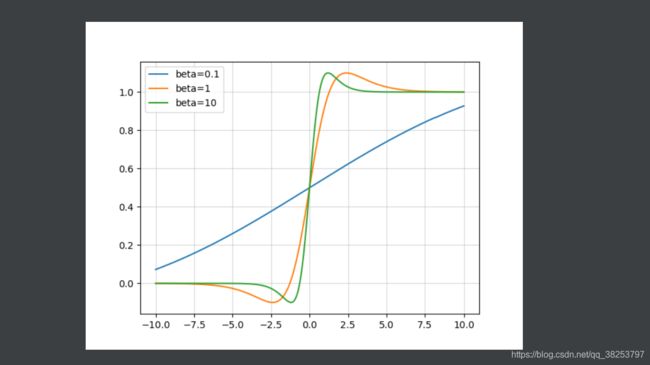
Swish函数梯度图像( β = 0.1 , β = 1 , β = 10 \beta=0.1, \beta=1,\beta=10 β=0.1,β=1,β=10)：

优点：

• 在x > 0的时候，同样是不存在梯度消失的情况；而在x < 0时候，神经元也不会像ReLU一样出现死亡的情况。
• 同时Swish相比于ReLU导数不是一成不变的，这也是一种优势。
• 而且Swish处处可导，连续光滑。

缺点：

• 计算量大，本来sigmoid函数就不容易计算，它比sigmoid还难。 2.8、hard-Swish

hard = 硬，就是让图像在整体上没那么光滑（从下面两个图都可以看出来）

函数表达式：

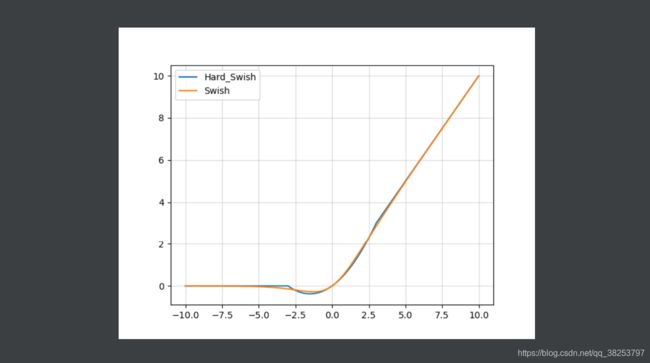
hard-Swish函数图像和Swish( β = 1 \beta=1 β=1)函数图像对比：

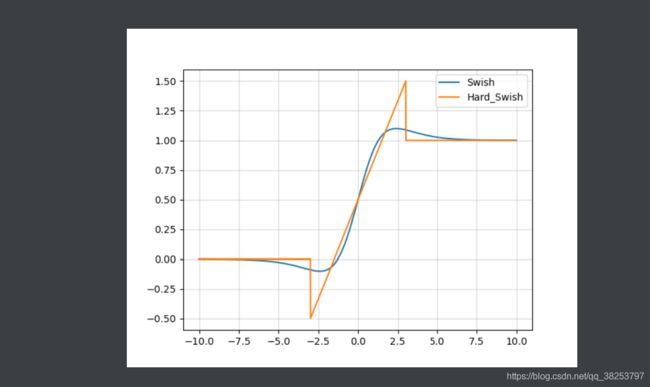
hard-Swish函数图像和Swish( β = 1 \beta=1 β=1)函数梯度图像对比：

优点：

1. hard-Swish近似达到了Swish的效果；
2. 且改善了Swish的计算量过大的问题，在量化模式下，ReLU函数相比Sigmoid好算太多了；

 2.9、Mish

论文地址：

https://arxiv.org/pdf/1908.08681.pdf

关于激活函数改进的最新一篇文章，且被广泛用于YOLO4中，相比Swish有0.494%的提升，相比ReLU有1.671%的提升。

Mish函数公式：

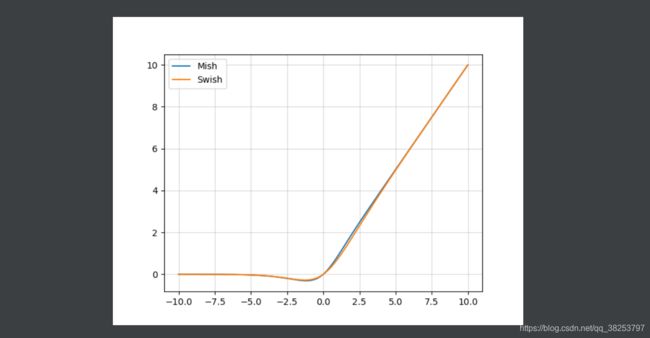
Mish函数图像和Swish( β = 1 \beta=1 β=1)函数图像对比：

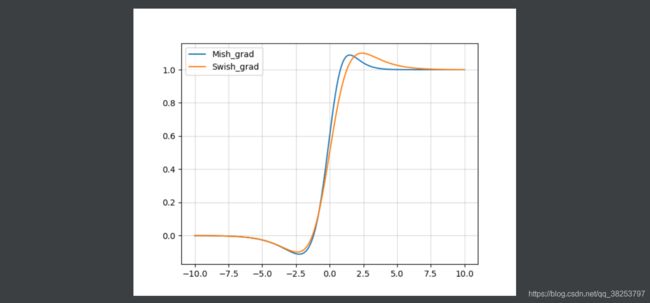
Mish函数图像和Swish( β = 1 \beta=1 β=1)函数导数图像对比：

为什么Mish表现的更好：

上面无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许更好的梯度流，而不是像ReLU中那样的硬零边界。
最后，可能也是最重要的，目前的想法是，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。Mish函数在曲线上几乎所有点上都极其平滑。

三、PyTorch 实现

import matplotlib.pyplot as plt
import numpy as np

class ActivateFunc():
    def __init__(self, x, b=None, lamb=None, alpha=None, a=None):
        super(ActivateFunc, self).__init__()
        self.x = x
        self.b = b
        self.lamb = lamb
        self.alpha = alpha
        self.a = a

    def Sigmoid(self):
        y = np.exp(self.x) / (np.exp(self.x) + 1)
        y_grad = y*(1-y)
        return [y, y_grad]

    def Hard_Sigmoid(self):
        f = (2 * self.x + 5) / 10
        y = np.where(np.where(f > 1, 1, f) < 0, 0, np.where(f > 1, 1, f))
        y_grad = np.where(f > 0, np.where(f >= 1, 0, 1 / 5), 0)
        return [y, y_grad]

    def Tanh(self):
        y = np.tanh(self.x)
        y_grad = 1 - y * y
        return [y, y_grad]

    def ReLU(self):
        y = np.where(self.x < 0, 0, self.x)
        y_grad = np.where(self.x < 0, 0, 1)
        return [y, y_grad]

    def ReLU6(self):
        y = np.where(np.where(self.x < 0, 0, self.x) > 6, 6, np.where(self.x < 0, 0, self.x))
        y_grad = np.where(self.x > 6, 0, np.where(self.x < 0, 0, 1))
        return [y, y_grad]

    def LeakyReLU(self):   # a大于1，指定a
        y = np.where(self.x < 0, self.x / self.a, self.x)
        y_grad = np.where(self.x < 0, 1 / self.a, 1)
        return [y, y_grad]

    def PReLU(self):    # a大于1，指定a
        y = np.where(self.x < 0, self.x / self.a, self.x)
        y_grad = np.where(self.x < 0, 1 / self.a, 1)
        return [y, y_grad]

    def ELU(self): # alpha是个常数，指定alpha
        y = np.where(self.x > 0, self.x, self.alpha * (np.exp(self.x) - 1))
        y_grad = np.where(self.x > 0, 1, self.alpha * np.exp(self.x))
        return [y, y_grad]

    def SELU(self):  # lamb大于1，指定lamb和alpha
        y = np.where(self.x > 0, self.lamb * self.x, self.lamb * self.alpha * (np.exp(self.x) - 1))
        y_grad = np.where(self.x > 0, self.lamb * 1, self.lamb * self.alpha * np.exp(self.x))
        return [y, y_grad]

    def Swish(self): # b是一个常数，指定b
        y = self.x * (np.exp(self.b*self.x) / (np.exp(self.b*self.x) + 1))
        y_grad = np.exp(self.b*self.x)/(1+np.exp(self.b*self.x)) + self.x * (self.b*np.exp(self.b*self.x) / ((1+np.exp(self.b*self.x))*(1+np.exp(self.b*self.x))))
        return [y, y_grad]

    def Hard_Swish(self):
        f = self.x + 3
        relu6 = np.where(np.where(f < 0, 0, f) > 6, 6, np.where(f < 0, 0, f))
        relu6_grad = np.where(f > 6, 0, np.where(f < 0, 0, 1))
        y = self.x * relu6 / 6
        y_grad = relu6 / 6 + self.x * relu6_grad / 6
        return [y, y_grad]

    def Mish(self):
        f = 1 + np.exp(x)
        y = self.x * ((f*f-1) / (f*f+1))
        y_grad = (f*f-1) / (f*f+1) + self.x*(4*f*(f-1)) / ((f*f+1)*(f*f+1))
        return [y, y_grad]

def PlotActiFunc(x, y, title):
    plt.grid(which='minor', alpha=0.2)
    plt.grid(which='major', alpha=0.5)
    plt.plot(x, y)
    plt.title(title)
    plt.show()

def PlotMultiFunc(x, y):
    plt.grid(which='minor', alpha=0.2)
    plt.grid(which='major', alpha=0.5)
    plt.plot(x, y)

if __name__ == '__main__':
    x = np.arange(-10, 10, 0.01)
    activateFunc = ActivateFunc(x)
    activateFunc.a = 100
    activateFunc.b= 1
    activateFunc.alpha = 1.5
    activateFunc.lamb = 2

    plt.figure(1)
    PlotMultiFunc(x, activateFunc.Sigmoid()[0])
    PlotMultiFunc(x, activateFunc.Hard_Sigmoid()[0])
    PlotMultiFunc(x, activateFunc.Tanh()[0])
    PlotMultiFunc(x, activateFunc.ReLU()[0])
    PlotMultiFunc(x, activateFunc.ReLU6()[0])
    PlotMultiFunc(x, activateFunc.LeakyReLU()[0])
    PlotMultiFunc(x, activateFunc.ELU()[0])
    PlotMultiFunc(x, activateFunc.SELU()[0])
    PlotMultiFunc(x, activateFunc.Swish()[0])
    PlotMultiFunc(x, activateFunc.Hard_Swish()[0])
    PlotMultiFunc(x, activateFunc.Mish()[0])

    plt.legend(['Sigmoid', 'Hard_Sigmoid', 'Tanh', 'ReLU', 'ReLU6', 'LeakyReLU',
                'ELU', 'SELU', 'Swish', 'Hard_Swish', 'Mish'])
    plt.show()

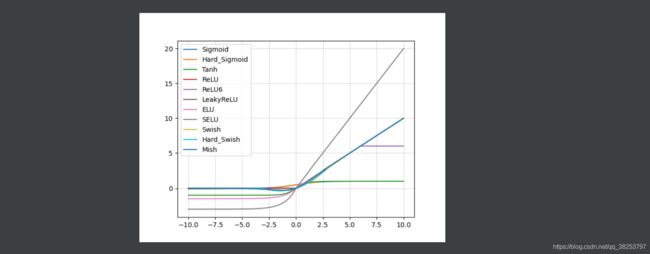
四、结果显示

Reference

链接1: link.

链接2: link.

https://arxiv.org/pdf/1908.08681.pdf

到此这篇关于YOLO v4常见的非线性激活函数详解的文章就介绍到这了,更多相关YOLO v4激活函数内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！