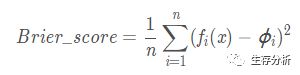svc预测概率_预测模型的概率校准
1.背景
机器学习分为:监督学习,无监督学习,半监督学习(也可以用hinton所说的强化学习)等。在这里,先简要介绍一下监督学习从给定的训练数据集中学习出一个函数(模型参数),当新的数据到来时,可以根据这个函数预测结果。监督学习的训练集要求包括输入输出,也可以说是特征和目标。训练集中的目标是由人标注的。监督学习就是最常见的分类(注意和聚类区分)问题,通过已有的训练样本(即已知数据及其对应的输出)去训练得到一个最优模型(这个模型属于某个函数的集合,最优表示某个评价准则下是最佳的),再利用这个模型将所有的输入映射为相应的输出,对输出进行简单的判断从而实现分类的目的。也就具有了对未知数据分类的能力。监督学习的目标往往是让计算机去学习我们已经创建好的分类系统(模型)。常见的有监督学习算法:回归分析和统计分类。
肿瘤预测模型是一个有监督学习模型,通过事先标注好的训练集,患者是否发生结局,患者信息等,训练一个COX模型,或者其他回归模型,在训练的模型基础上进行预测输出。在预测模型搭建过程中,由于抽样与正则化的原因,导致模型输出的概率值明显偏离真实的概率值。这时候我们称这些模型直接输出的概率值是定序值,而非定距数值,可比较大小,但其绝对值并无太多含义。那么如何将模型输出的prob校准到真实的逾期概率呢。使得经过校准后的概率变成逾期概率的意义。比如预测模型预测某个样本属于正类的概率是0.8,那么就应当说明有80%的把握认为该样本属于正类,或者100个概率为0.8的里面有80个确实属于正类。根据这个关系,可以用测试数据得到Probability Calibration curves。
假设我们考虑这样的一种情况:在二分类中,属于类别0的概率为0.500001,属于类别1的概率为0.499999。假若按照0.5作为判别标准,那么毋庸置疑应该划分到类别0里面,但是这个真正的分类却应该是1。如果我们不再做其他处理,那么这个就属于错误分类,降低了算法的准确性。如果在不改变整体算法的情况下,我们是否能够做一些补救呢?或者说验证下当前算法已经是最优的了呢?这个时候就用到了概率校准。
2.案例
如下表所示,
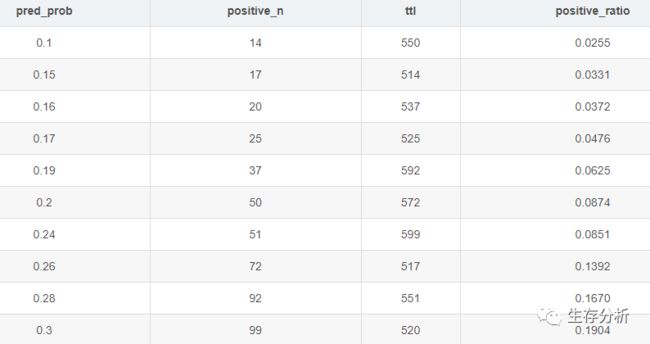
pred_prob为预测模型输出的预测概率predict probability
在数据集中预测概率为pred_prob的总数为ttl,例如第一行ttl的550意思预测概率为0.1的总例数为550条观测,其中有positive_n阳性例数,正例占比positive_ratio =positive_n/ttl
如上表,模型输出的pred_prob = 0.1 对应真实结局发生率 0.0255
模型解决了数据的排序问题【随着预测概率的增加,真实概率也在增加】,但从这个例子我们可以看出,模型预测与真实值之间出现了很大的差异。
那么我们如何将模型预测的概率f(x) 校准到 Real_Proba,数学上我们只需要找到一个f(x) ~ Real_Proba的映射关系,也就是说找到一个g(x),其中g(x)中的x为f(x),也就是说利用f(x) ~ Real_Proba的对应关系,拟合一个函数g(x),将f(x)校准到Real_Proba。
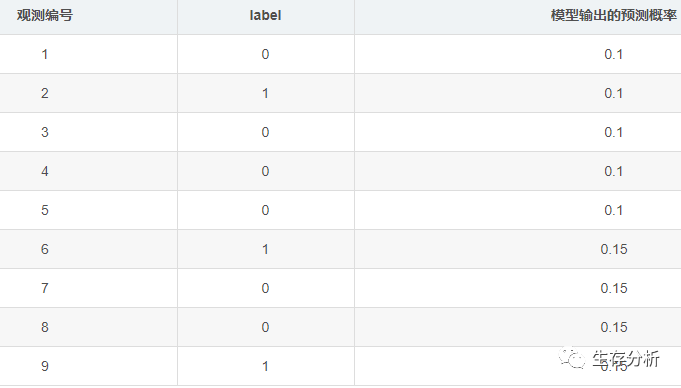
实案例中,我们并不知道观测结局的真实发生率,但是我们有患者发生结局事件标签label,通常我们的数据组织形式如下:
label=0 和label=1真实数据的两个结局,我们需要利用模型的预测值 与 label进行模型搭建。
3.校准方法
4.校准评价指标---Brier分数
Brier分数是衡量概率校准的一个参数。
校准函数公式
其中n为观测个数,fi(x)为第i个观测的预测值,φi为第i个观测对应的真实发生的label(0/1).Brier_score越低说明预测值与真实值越接近,预测概率越准确。简单来说,Brier分数可以被认为是对一组概率预测的“校准”的量度,或者称为“ 成本函数 ”,这一组概率对应的情况必须互斥,并且概率之和必须为1。
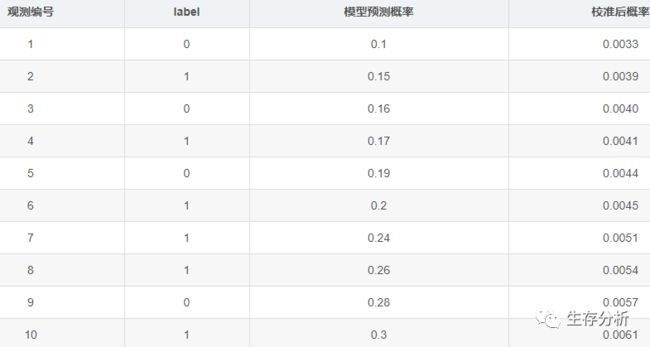
从这个案例可以看出,模型校准后,Brier Score在增大,所以不校准模型结果更优。
在说概率校准前,先说下Brier分数,因为它是衡量概率校准的一个参数(该案例中的校准概率并未真实计算,只是用来举例)。
再引用维基百科的一个例子说明 Brier分数的计算方式:
假设一个人预测在某一天会下雨的概率P,则Brier分数计算如下:
如果预测为100%(P = 1),并且下雨,则Brier Score为0,可达到最佳分数。
如果预测为100%(P = 1),但是不下雨,则Brier Score为1,可达到最差分数。
如果预测为70%(P = 0.70),并且下雨,则Brier评分为(0.70-1)2 = 0.09。
如果预测为30%(P = 0.30),并且下雨,则Brier评分为(0.30-1)2 = 0.49。
如果预测为50%(P = 0.50),则Brier分数为(0.50-1)2 =(0.50-0)2 = 0.25,无论是否下雨。
概率校准就是对分类函数做出的分类预测概率重新进行计算,并且计算Brier分数,然后依据Brier分数的大小判断对初始预测结果是支持还是反对。
3.常用模型的表现
以下图表比较了校准不同预测模型预测概率的良好程度:
第一张图是概率校准曲线,说明实际概率与预测概率的关系。可见Logistic回归预测概率比较准(模型本身的特点),朴素贝叶斯过于自信(可能由于冗余特征所致,违背了特征独立性前提)呈反sigmoid曲线,SVM很不自信呈sigmoid曲线,随机森林也是。
第二张图是预测概率分布图,Logistic和朴素贝叶斯大多分布在0或1附近,都是比较自信的,而随机森林多分布在0.2或0.8附近,SVM很不自信主要分布在0.5附近。
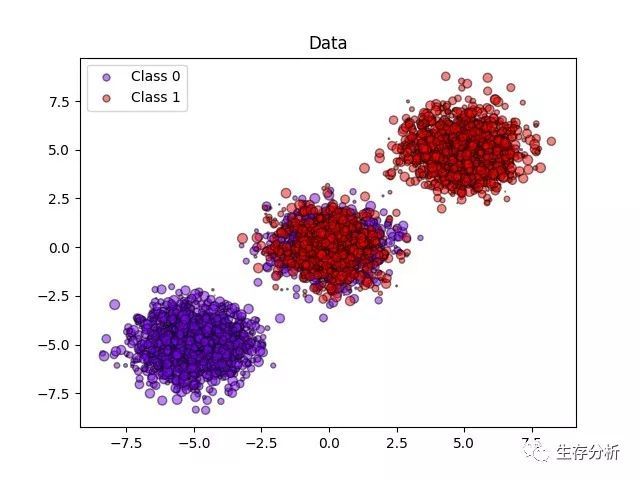
以下图像展示了概率校准的好处. 第一个图像显示一个具有 2 个类和 3 个数据块的数据集. 中间的数据块包含每个类的随机样本. 此数据块中样本的概率应为 0.5.
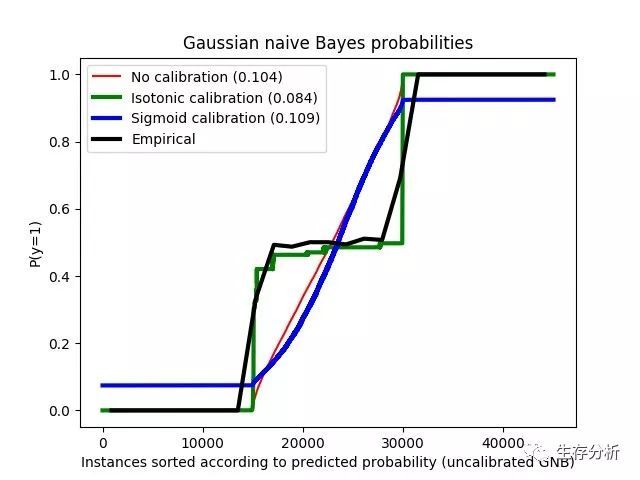
以下图像使用没有校准的高斯朴素贝叶斯分类器, 使用 sigmoid 校准和非参数的等渗校准来显示上述估计概率的数据. 可以观察到, 非参数模型为中间样本提供最准确的概率估计, 即0.5.
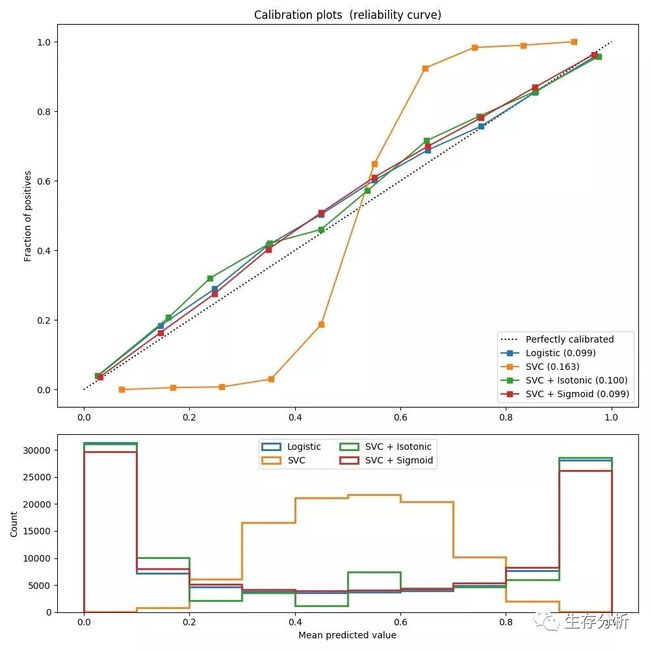
对具有20个特征变量的100.000个样本(其中一个用于模型拟合)进行二元分类的模拟数据集进行以下实验. 在 20个特征中,只有 2 个是信息量, 10 个是冗余的. 该图显示了使用逻辑回归获得的估计概率, 线性支持向量分类器(SVC)和具有 sigmoid 校准和 sigmoid 校准的线性 SVC. 校准性能使用 Brier score来计算, 请看下面的图例(越销越好)
这里可以观察到, 逻辑回归被很好地校准, 因为其曲线几乎是对角线. 线性 SVC 的校准曲线或可靠性图具有 sigmoid 曲线, 这是一个典型的不够自信的分类器. 在 LinearSVC 的情况下, 这是 hinge loss 的边缘属性引起的, 这使得模型集中在靠近决策边界(支持向量)的 hard samples(硬样本)上. 这两种校准都可以解决这个问题, 并产生几乎相同的结果. 下图显示了高斯朴素贝叶斯在相同数据上的校准曲线, 具有两种校准, 也没有校准.
可以看出, 高斯朴素贝叶斯的表现非常差, 但是以线性 SVC 的方式也是如此. 尽管线性 SVC 显示了 sigmoid 校准曲线, 但高斯朴素贝叶斯校准曲线具有转置的 sigmoid 结构. 这对于过分自信的分类器来说是非常经典的. 在这种情况下,分类器的过度自信是由违反朴素贝叶斯特征独立假设的冗余特征引起的.
用等渗回归法对高斯朴素贝叶斯概率的校准可以解决这个问题, 从几乎对角线校准曲线可以看出. Sigmoid 校准也略微改善了 brier 评分, 尽管不如非参数等渗校准那样强烈. 这是 sigmoid 校准的固有限制,其参数形式假定为 sigmoid ,而不是转置的 sigmoid 曲线. 然而, 非参数等渗校准模型没有这样强大的假设, 并且可以处理任何形状, 只要有足够的校准数据. 通常,在校准曲线为 sigmoid 且校准数据有限的情况下, sigmoid 校准是优选的, 而对于非 sigmoid 校准曲线和大量数据可用于校准的情况,等渗校准是优选的.
CalibratedClassifierCV 也可以处理涉及两个以上类的分类任务, 如果基本估计器可以这样做的话. 在这种情况下, 分类器是以一对一的方式分别对每个类进行校准. 当预测未知数据的概率时, 分别预测每个类的校准概率. 由于这些概率并不总是一致, 因此执行后处理以使它们归一化.
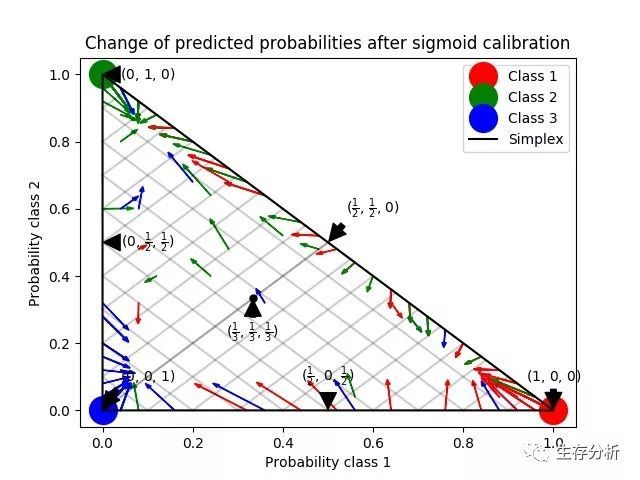
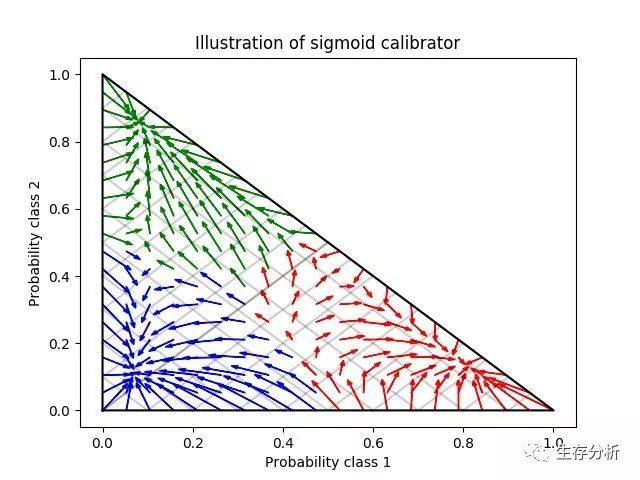
下一个图像说明了 Sigmoid 校准如何改变 3 类分类问题的预测概率. 说明是标准的 2-simplex,其中三个角对应于三个类. 箭头从未校准分类器预测的概率向量指向在保持验证集上的 sigmoid 校准之后由同一分类器预测的概率向量. 颜色表示实例的真实类(red: class 1, green: class 2, blue: class 3).
基础分类器是具有 25 个基本估计器(树)的随机森林分类器. 如果这个分类器对所有 800 个训练数据点进行了训练, 那么它的预测过于自信, 从而导致了大量的对数损失. 校准在 600 个数据点上训练的相同分类器, 其余 200 个数据点上的 method =’sigmoid’ 减少了预测的置信度, 即将概率向量从单面的边缘向中心移动:
该校准导致较低的 log-loss(对数损失). 请注意,替代方案是增加基准估计量的数量, 这将导致对数损失类似的减少.
本公众号部分精彩历史文章:
04:如何在R软件中求一致性指数(Harrell'concordance index:C-index)?
05:Nomogram 绘制原理及R&SAS实现.
06 :Lasso方法简要介绍及其在回归分析中的应用
07 : 最优模型选择中的交叉验证(Cross validation)方法
08 : 用R语言进行分位数回归(Quantile Regression)
09 : 样本数据中异常值(Outliers)检测方法及SPSS & R实现
10 : 原始数据中几类缺失值(Missing Data)的SPSS及R处理方法
11 : [Survival analysis] Kaplan-Meier法之SPSS实现
12 : [Survival analysis] COX比例风险回归模型在SPSS中的实现
13 : 用R绘制地图:以疾病流行趋势为例
14 : 数据挖掘方法:聚类分析简要介绍 及SPSS&R实现
15 : 医学研究中的Logistic回归分析及R实现
16 : 常用的非参数检验(Nonparametric Tests)总结
17 : 高中生都能看懂的最小二乘法原理
18 : R语言中可实现的常用统计假设检验总结(侧重时间序列)
19 : 如何根据样本例数、均数、标准差进行T-Test和ANOVA
20 : 统计学中自由度的理解和应用
21 : ROC和AUC介绍以及如何计算AUC
22 : 支持向量机SVM介绍及R实现
23 : SPSS如何做主成分分析?
24 : Bootstrap再抽样方法简介
25 : 定量测量结果的一致性评价及 Bland-Altman 法的应用
26 : 使用R绘制热图及网络图
27 : 几种常用的双坐标轴图形绘制
28 : 遗失的艺术—诺谟图(Nomogram)
29 : Nomogram 绘制原理及R&SAS实现(二)
30 : WOE:信用评分卡模型中的变量离散化方法
31 : 结构方程模型(SEM)简介及教程下载
32 : 重复测量的多因素方差分析SPSS实现操作过程
回复文章前代码数字如“04”即可查看或直接查看历史文章。
公众号:survival-analysis QQ:8243033
邮箱:8243033 @ qq.com 欢迎关注!