技术交流QQ群:1027579432，欢迎你的加入！
欢迎关注我的微信公众号：CurryCoder的程序人生
一.原理
- 假设初始待排序数据有n个，可以将n个数据看成n个独立的子序列，因此每个子序列的长度为1，然后两两合并，得到[n/2]个长度为2或1(注意如果n为奇数时，就会出现多出一个元素无法与其他元素合并)的有序子序列;再两两合并，一种重复下去，直到得到一个长度为n的有序序列为止，这种排序方法为2路排序方法。
归并排序过程.jpg
二.递归方法来实现归并排序
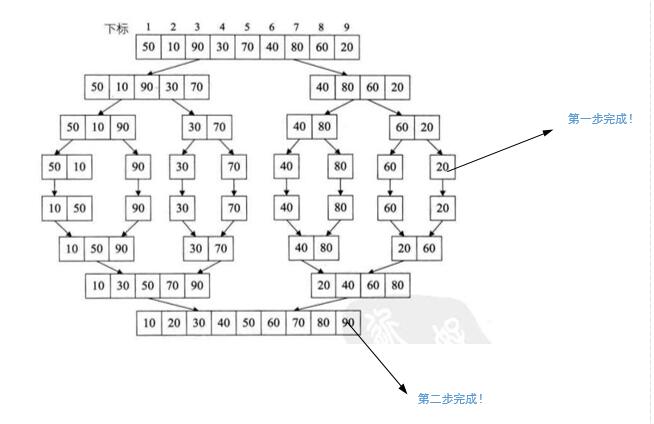
- 原理：使用递归方法来实现归并排序时，核心思想是两个有序子序列的合并，注意这里是有序子序列的合并，因此下面要做两件事，整个过程如下图所示：
- (1)将待排序序列从中间一分为二，对左右两边再进行递归分割操作，得到n个相互独立的子序列；
-
(2)对n个独立的子序列递归的执行合并操作，最终得到有序的序列。
递归方法实现归并排序.jpg
-
程序的伪代码如下图所示，其中函数Merge_Sort()是统一的函数接口，便于用户调用；函数Msort()首先递归的得到n个独立子序列，然后使用Merge()函数实现有序子序列归并。
Merge函数.jpg
Msort函数.jpg
Merge_Sort函数.jpg
三.非递归方法实现归并排序
- 递归方法的不足：递归方法实现归并排序代码容易理解，但是递归容易浪费空间，比如上述递归方法实现归并排序的第二步中，每一步合并都必须创建一个临时数组TmpA，此数组用来暂存已经排好序的中间序列。然后等中间序列排好序后，再将临时数组TmpA中的结果重新导回到数组A中。接下来递归的执行上面的合并操作，直到序列完全排好序。但是，整个归并排序过程中的空间复杂度太大为O(n)。
-
解决方法：非递归方法实现归并排序时，在第二步时可以采用下面的思想，不用在每一次归并时都创建一个临时数组TmpA，临时数组TmpA只被创建一次，每次执行完归并操作后，将归并的结果暂存在数组TmpA中，然后进行下一次归并操作时，先将TmpA中的上一次归并好的结果重新导回到数组A中，再进行归并操作。整个过程的空间复杂度将变小，不用每次操作都创建一个临时数组TmpA。当归并操作执行到最后一次时，如果此时已经排好序的序列在数组A中，则不用再重新导回到数组A中；如果此时已经排好序的序列在数组TmpA中，则在执行一次导回操作，将数组TmpA中的结果重新导回到数组A中，完成整个排序。这个过程的伪代码如下：
非递归方法实现归并排序.jpg
四.两种方法实现的归并排序代码如下:
#include
#include
using namespace std;
#define N 9
#define MAXSIZE 10
typedef struct
{
int r[MAXSIZE + 1];
int len;
} Sqlist;
void show(Sqlist L)
{
for (int i = 1; i <= L.len; i++)
cout << L.r[i] << " ";
cout << endl;
}
// 归并操作
void Merge(int A[], int TempA[], int L, int LeftEnd, int RightEnd)
{ // L：左边子序列的起点；LeftEnd：左边子序列的终点
int k, j; // k是数组tempA左边起点，j是右边子序列的的起点，RightEnd:右边子序列的终点
for (j = LeftEnd + 1, k = L; L <= LeftEnd && j <= RightEnd; k++)
{
if (A[L] < A[j])
TempA[k] = A[L++];
else
TempA[k] = A[j++];
}
if (L <= LeftEnd)
{
for (int l = 0; l <= LeftEnd - L; l++)
TempA[k + l] = A[L + l];
}
if (j <= RightEnd)
{
for (int r = 0; r <= RightEnd - j; r++)
TempA[k + r] = A[j + r];
}
}
// 递归方法实现
// 归并排序整个操作
void Msort(int A[], int TempA[], int L, int RightEnd)
{
int center;
int TempA2[MAXSIZE + 1];
if (L == RightEnd)
TempA[L] = A[L];
else
{
center = (L + RightEnd) / 2;
Msort(A, TempA2, L, center);
Msort(A, TempA2, center + 1, RightEnd);
Merge(TempA2, TempA, L, center, RightEnd);
}
}
// 统一函数接口
void MergeSort(Sqlist *L)
{
Msort(L->r, L->r, 1, L->len);
}
// 非递归方法实现
void MergePass(int A[], int TempA[], int length, int n)
{
// length:当前子序列的长度 n:待排序列中的元素个数
int i = 1;
while (i <= n - 2 * length - 1)
{ // 子序列的个数是偶数个
Merge(A, TempA, i, i + length - 1, i + 2 * length - 1);
i = i + 2 * length;
}
if (i < n - length + 1) // 归并最后两个子序列
Merge(A, TempA, i, i + length - 1, n);
else
{ // 最后只剩下一个子序列
for (int j = i; j <= n; j++)
TempA[j] = A[j];
}
}
// 统一函数接口
void MergeSort1(Sqlist *L)
{
int *TempA = (int *)malloc(L->len * sizeof(int));
int length = 1; // 初始子序列的长度
while (length < L->len)
{
MergePass(L->r, TempA, length, L->len);
length *= 2;
MergePass(TempA, L->r, length, L->len);
length *= 2;
}
}
int main()
{
Sqlist L;
int d[N] = {50, 10, 90, 30, 70, 40, 80, 60, 20};
for (int i = 0; i < N; i++)
L.r[i + 1] = d[i];
L.len = N;
cout << "归并排序前(递归方法): ";
show(L);
cout << "归并排序后(递归方法): ";
MergeSort(&L);
show(L);
cout << "-------------------------------------------------\n";
cout << "归并排序前(非递归方法): ";
show(L);
cout << "归并排序后(非递归方法): ";
MergeSort1(&L);
show(L);
return 0;
}
- STL实现
#include
using namespace std;
// 归并排序：把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。
// 迭代方法实现
template
void MergeSort(T arr[], int len){
T* a = arr; // 指针a指向原始数组
T* b = new T[len]; // 指针b指向新创建的一个数组
for(int seg=1; seg < len; seg+=seg){
for(int start=0; start < len; start += seg + seg){
int low = start;
int mid = min(start+seg, len);
int high = min(start+seg+seg, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid+1, end2 = high;
while(start1 < end1 && start2 < end2){
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
}
while(start1 < end1){
b[k++] = a[start1++];
}
while(start2 < end2){
b[k++] = a[start2++];
}
}
T* temp = a;
a = b;
b = temp;
}
if(a != arr){
for(int i=0; i < len; i++){
b[i] = a[i];
}
b = a;
}
delete[] b;
}
// 递归方法实现
template
void MergeSortRecursiveCore(T arr[], T reg[], int start, int end){
if(start >= end){
return;
}
int len = end - start;
int mid = start + (len >> 1);
int start1 = start, end1 = mid;
int start2 = mid+1, end2 = end;
MergeSortRecursiveCore(arr, reg, start1, end1);
MergeSortRecursiveCore(arr, reg, start2, end2);
int k = start;
while(start1 <= end1 && start2 <= end2){
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
}
while(start1 <= end1){
reg[k++] = arr[start1++];
}
while(start2 <= end2){
reg[k++] = arr[start2++];
}
for(k = start; k<=end; k++){
arr[k] = reg[k];
}
}
template
void MergeSortRecursive(T arr[], const int len){
T* reg = new T[len];
MergeSortRecursiveCore(arr, reg, 0, len-1);
delete[] reg;
}
五、归并排序时间复杂度总结：
- 平均时间复杂度：O(nlogn)
- 最好情况：O(nlogn)
- 最坏情况：O(nlogn)
- 空间复杂度：O(n)
- 稳定性：稳定