机器学习-线性回归模型

线性回归模型

简述

• **线性回归(Linear Regression)**是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

• 线性回归利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模。 这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。

• 图解

  

使用场景

线性回归有很多实际的用途，分为以下两类：

1. 如果目标是预测或者映射，线性回归可以用来对观测数据集的y和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。

2. 给定一个变量y和一些变量X1, ⋯ , ,这些变量有可能与y相关，线性回归分析可以用来量化y与X 之间相关性的强度，评估出与y不相关的X ，并识别出哪些X的子集包含了关于y的冗余信息。

线性回归方程

模型 Hypothesis

$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

模型参数 Parameters

$${\theta }_0,{\theta }_1$$

代价函数 Cost Funciton

$$\mathrm{J}\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$$

目标 Goal

$$\underset{{\theta }_0,{\theta }_1}{\mathrm{minimize}}\mathrm{J}({\theta }_0,{\theta }_1)$$

工作方式

描述回归问题的标记如下：

• 代表训练集中实例的数量
• 代表特征/输入变量
• 代表目标变量/输出变量
• (, ) 代表训练集中的实例
• ((), ()) 代表第 个观察实例
• ℎ 代表学习算法的解决方案或函数也称为假设（ hypothesis）

这是监督学习算法的工作方式，将训练集里房屋价格输出给学习算法，学习算法开始执行，然后输出一个函数，通常表示为小写 ℎ表示。

代价函数

​ 为模型选择合适的参数（paramters），在单变量线性回归问题便是直线的斜率和在y轴上的截距。

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是模型误差（modeling error）。

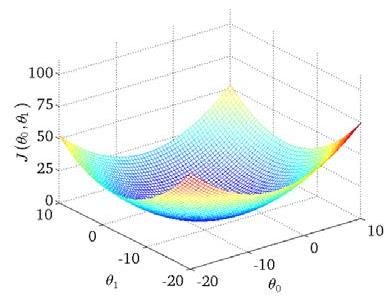
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得公式(3)最小。

​ 可以看出在三维空间中存在一个使得(0, 1)最小的点。

**代价函数也被称为平方误差函数，有时也被称为平方误差代价函数。**我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好好地发挥作用，但是平方误差代价函数可能是解决回归问题的最常会用的手段了。

线性回归评价方法

常见评价指标

单变量线性回归案例-波士顿房价预测

背景介绍

与房价密切相关的除了单位的房价，还有房屋的尺寸。可以根据已知的房屋成交价和房屋的尺寸进行线性回归，继而可以对已知房屋尺寸，而未知房屋成交价格的实例进行成交价格的预测。

数据准备

成交信息只使用房屋的面积以及对应的成交价格。

• 房屋面积单位为平方英尺（ ft2）

• 房屋成交价格单位为万

实验过程

可行性分析

• 简单而直观的方式是通过数据的可视化直接观察房屋成交价格与房屋尺寸间是否存在线性关系；
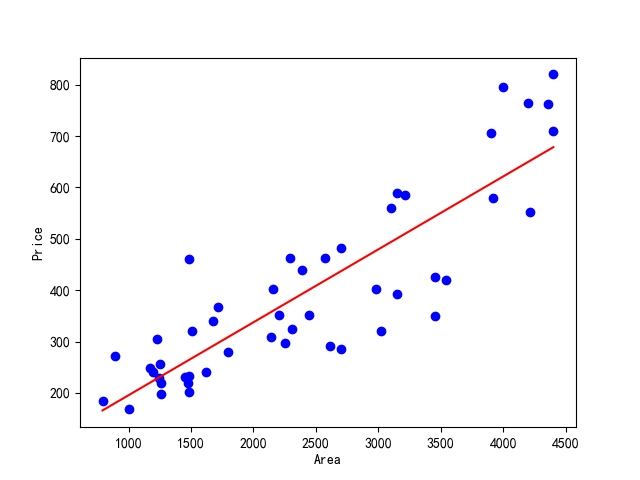
• 通过绘制散点图可以很好的在二维平面中进行可视化展示。

下右图为数据的散点图，其中横坐标为房屋面积，纵坐标为房屋的成交价格。可以看出，靠近坐标左下角部分的点，表示房屋尺寸较小的房子，其对应的房屋成交价格也相对较低。同样的，靠近坐标右上部分的点对应于大尺寸高价格的房屋。从总体来看，房屋的面积和成交价格基本成正比。

目标

对房屋成交信息建立回归方程，根据房屋面积预测房屋价格

结果展示

模型评估

回归系数

回归系数（regression coefficient）在回归方程中表示自变量x 对因变量y 影响大小的参数。回归系数越大表示x 对y 影响越大，正回归系数表示y 随x 增大而增大，负回归系数表示y 随x增大而减小。例如回归方程式Y=bX+a中，斜率b称为回归系数，表示X每变动一单位，平均而言，Y将变动b单位。

技术路线一 Python sklearn

代码

# -*- coding:utf-8 -*-

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression as LR
from sklearn.metrics import mean_squared_error, r2_score

# 加载数据
data = pd.read_csv('../data/prices.csv')
# 训练数据
dataset_X = data['房屋面积'].astype(int).values
# 目标值
dataset_Y = data['交易价格'].astype(int).values
# 矩阵变形
dataset_X = dataset_X.reshape(len(dataset_X), 1)

# 建立线性回归模型
lr = LR()
# 训练模型
lrModel = lr.fit(dataset_X, dataset_Y)
# 使用训练的模型进行预测
data['预测房价'] = lr.predict(dataset_X)
print(data[:20])
# 打印回归模型的 回归系数和截距
print('Coefficients: %d  intercept: %d ' % (lr.coef_, lr.intercept_))
# 评估模型
# 计算模型误差
print("MSE: ", mean_squared_error(data['交易价格'], data['预测房价']))
# 计算模型的r2
print("r2: ", r2_score(data['交易价格'], data['预测房价']))
# 设置绘图参数
# 设置中文显示
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
# 绘制 房屋尺寸和房屋面积的散点图
plt.scatter(dataset_X, dataset_Y, c='b')
plt.title("线性回归预测图")
plt.xlabel("房屋尺寸")
plt.ylabel("房屋价格")
# 绘制房屋价格的直线
plt.plot(dataset_X, data['预测房价'], c='r')
plt.show()

结果

编号  房屋面积  交易价格        预测房价
0    1  1000   168  195.423832
1    2   792   184  165.890433
2    3  1260   197  232.340580
3    4  1262   220  232.624555
4    5  1240   228  229.500830
5    6  1170   248  219.561705
6    7  1230   305  228.080955
7    8  1255   256  231.630642
8    9  1194   240  222.969405
9   10  1450   230  259.318203
10  11  1481   202  263.719816
11  12  1475   220  262.867891
12  13  1482   232  263.861803
13  14  1484   460  264.145778
14  15  1512   320  268.121428
15  16  1680   340  291.975327
16  17  1620   240  283.456077
17  18  1720   368  297.654826
18  19  1800   280  309.013826
19  20  4400   710  678.181306
Coefficients: 0  intercept: 53 
MSE:  7581.861759164643
r2:  0.7520517837722847