数字图像处理——第七章小波和多分辨率处理

7.1 背景

我们观察图像时，小的物体我们以较高的分辨率来观察，大的物体以较低的分辨率来观察，当图像中同时存在大和小的物体时，以不同的分辨率来观察将更具优势。
计算机处理的图像模型是具有局部变换特性的亮度值的二维阵列，局部直方图在不同的区域下变换可能很明显，这就使得为整幅图像建立统计模型造成困难，那么我们就引入图像金字塔这一统计工具来为图像建立统计特性模型。

7.1.1 图像金字塔

在说明什么是图像金字塔的过程之前，我们需要需要了解一个概念：尺度

尺度，顾名思义就是说图像的尺寸和分辨率。在我们进行图像处理的时候，会经常对源图像的尺寸进行放大或者缩小的变换，进而转换为我们指定尺寸的目标图像。在对图像进行放大和缩小的变换的这个过程，我们称为尺度调整。

而图像金字塔则是图像多尺度调整表达的一种重要的方式，图像金字塔方法的原理是：将参加融合的的每幅图像分解为多尺度的金字塔图像序列，将低分辨率的图像在上层，高分辨率的图像在下层，上层图像的大小为前一层图像大小的1/4。层数为0,1,2……N。将所有图像的金字塔在相应层上以一定的规则融合，就可得到合成金字塔，再将该合成金字塔按照金字塔生成的逆过程进行重构，得到融合金字塔。
如图所示：分辨率高的将在图像金字塔的下层，分辨率低的在上层。

import cv2 as cv
#高斯金字塔
def pyramid_demo(image):
    level = 3      #设置金字塔的层数为3
    temp = image.copy()  #拷贝图像
    pyramid_images = []  #建立一个空列表
    for i in range(level):
        dst = cv.pyrDown(temp)   #先对图像进行高斯平滑，然后再进行降采样（将图像尺寸行和列方向缩减一半）
        pyramid_images.append(dst)  #在列表末尾添加新的对象
        cv.imshow("pyramid"+str(i), dst)
        temp = dst.copy() #降采样保留
    return pyramid_images
img01=cv.resize(img,(512,512)) #图像修改为2的n次方，长和宽相等
pyramid_demo(img01)
cv.waitKey(0)
cv.destroyAllWindows()

图像被修建为3个不同分辨率的窗口，下图为底层图像。

7.1.2 子带编码

一幅图像被分解为一组频带受限的分量，称为子带。
■ 子带可以重组在一起无失真地重建原始图象
■ 每个子带通过对输入进行带通滤波而得到
■ 子带带宽小于原始图像带宽，子带可以进行无信息损失的抽样
■ 原始图象的重建可以通过内插、滤波、和叠加单个子带来完成

上路是低通滤波，下路是高通滤波，输出为重构结果。
采用z变换：


无失真重建条件：

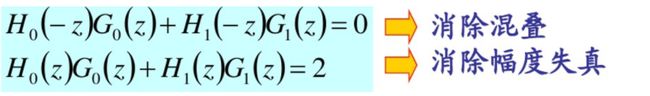
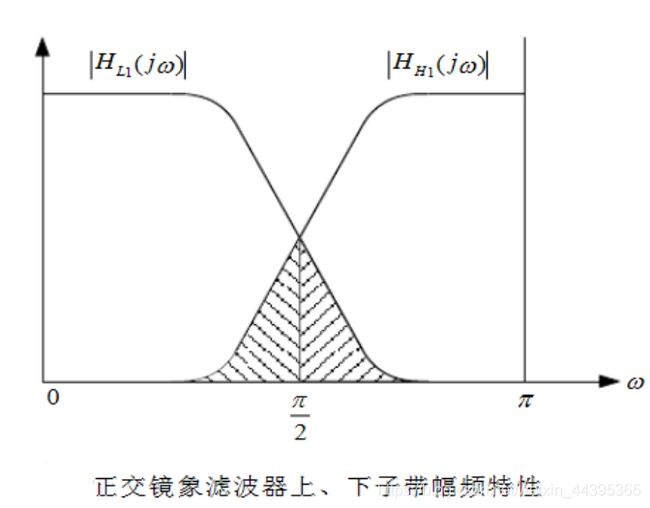
一维滤波器也通过构建垂直、水平方向的滤波器来达到正交的效果

7.1.3 哈尔变换

$T=HF{H}^T$,F是一个N x N图像矩阵，H是一个N x N哈尔变换矩阵，T是一个N x N变换结果。
数学上的例子展示一下：
例如我们有一个一维的图像[2,4,6,8,10,12,14,16].

求均值：我们求相邻像素的均值[3,7,11,15]。这个新的图像分辨率就成了原来的一半(8/2=4)。

求差值。上面的均值我们存储了图像的整体信息。但是很多细节信息我们丢掉了，所以我们同时要记录图像的细节信息，这样在重构时能够恢复图像的全部信息。下面是求第m个差值的公式：

b[m]=(a[2m]−a[2m+1])/2b[m]=(a[2m]−a[2m+1])/2

经过计算我们得到了结果[-1,-1,-1,-1]。这个新的分辨率也成了原来的一半(8/2=4)。

此时上面两步形成了第一次分解的结果[3,7,11,15,-1,-1,-1,-1]。包含了图像的整体信息和细节信息。接下来的分解我们重复1,2步，将整体信息再次进行分解，得到了二级分解结果[5，13，-2，-2].同样的，前面的[5,13]是整体信息，后面的[-2,-2]是细节信息。
不断得分解，我们得到不同分辨率的整体信息和细节，直到分辨率为1。

#读取灰度图
from pywt import dwt2
img = cv.imread('pic/house500x500.jpg',0)

#cA，cH,cV,cD 分别为近似分量(低频分量)、水平细节分量、垂直细节分量和对角细节分量
cA,(cH,cV,cD)=dwt2(img,'haar')#dwt2函数第二个参数指定小波基

#打印语句
plt.subplot(232), plt.imshow(cA, 'gray'), plt.title('cA')
plt.subplot(233), plt.imshow(cH, 'gray'), plt.title('cH')
plt.subplot(234), plt.imshow(cV, 'gray'), plt.title('cV')
plt.subplot(235), plt.imshow(cD, 'gray'), plt.title('cD')

7.2 多分辨率展开

◆图像金字塔、子带编码和哈尔变换，在数学理论多分辨率分析中扮演了重要角色。
◆在多分辨率分析( MRA )中，尺度函数被用于建立某一函数或图像的一系列近似值，相邻两近似值之间的近似度相差2倍。
◆被称为小波的附加函数用于对相邻近似值之间的差异进行编码

7.3 小波展开

小波序列展开：

展开系数计算：

离散小波变换：

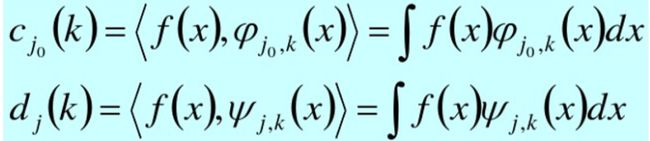
连续小波变换：

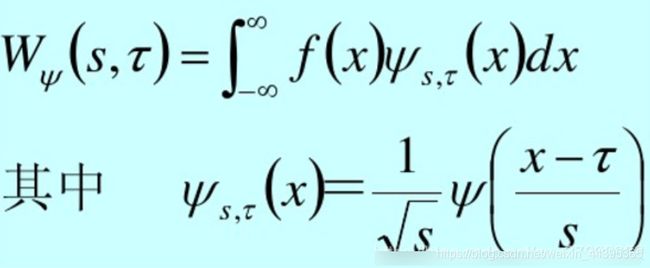
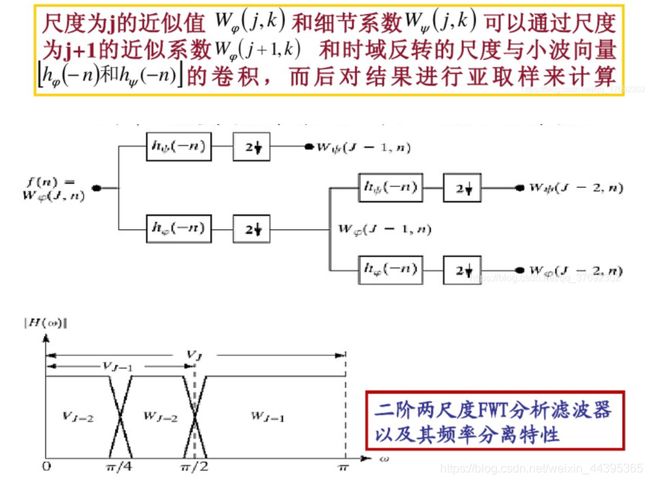
快速小波变换：


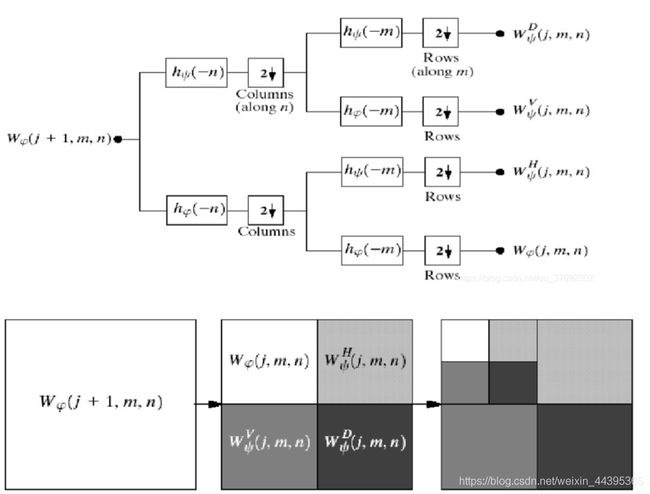
二维小波变换示意图：

7.4 小波包

小波变换只对信号的低频部分做进一步分解，而对高频部分也即信号的细节部分不再继续分解，所以小波变换能够很好地表征一大类以低频信息为主要成分的信号，不能很好地分解和表示包含大量细节信息（细小边缘或纹理）的信号，如非平稳机械振动信号、遥感图象、地震信号和生物医学信号等。

小波包变换既可以对低频部分信号进行分解，也可以对高频部分进行分解，而且这种分解既无冗余，也无疏漏，所以对包含大量中、高频信息的信号能够进行更好的时频局部化分析。

7.4 小波工具箱学习

[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wname) #wfilters 小波滤波器
输出Lo_D，Hi_D，Lo_R和Hi_R是行向量，分别返回与wname相关低通分解、高通分解、低通重构和高通重构滤波器。wname是正交或双正交小波的名字
[F1,F2] = wfilters(wname,type),type可取’d’(分解)、‘r’（重构）、‘l’（低通）、‘h’（高通）四种值，分解或低通滤波器在F1中返回，重构或高通滤波器放在F2中。
wavedec2 二维多尺度分解
wavedec2 可直接处理彩色图像
[C,S] = wavedec2(X,N,wname) % 对图像X用wname小波基函数实现N尺度（级数）分解。
[C,S] = wavedec2(X,N,Lod,Hid) % 用特定的低通和高通滤波器（Lod和Hid）进行小波分解。

import cv2
import pywt
img = cv2.imread("pic/house500x500.jpg")
img = cv2.resize(img, (448, 448))
# img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB).astype(np.float32)
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY).astype(np.float32)

plt.figure('二维图像多级分解')
coeffs = pywt.wavedec2(img, 'haar', level=2)
cA2, (cH2, cV2, cD2), (cH1, cV1, cD1) = coeffs

# 将每个子图的像素范围都归一化到与CA2一致  CA2 [0,255* 2**level]
AH2 = np.concatenate([cA2, cH2+510], axis=1)
VD2 = np.concatenate([cV2+510, cD2+510], axis=1)
cA1 = np.concatenate([AH2, VD2], axis=0)

AH = np.concatenate([cA1, (cH1+255)*2], axis=1)
VD = np.concatenate([(cV1+255)*2, (cD1+255)*2], axis=1)
img = np.concatenate([AH, VD], axis=0)

plt.imshow(img,'gray')
plt.title('2D WT')
plt.show()

二维图像多维分解结果：

总结

与基函数为正弦函数的傅里叶变换不同，小波变换的基函数是小型波，即小波，它具有变换的频率和有限的持续时间，而傅里叶变换则丢失了时间信息。小波变换是基于多分辨率理论的信号处理和分析方法的基础，包括子代编码、数字语音识别的正交镜像滤波及金字塔图像处理，多分辨率下检测信号的特性是很容易的，本章的内容集中于离散小波变换，小波变换的用途很多，如图像编码、噪声去除、边缘检测、图像压缩等。小波必须满足两个特点：震荡及短暂非零。它通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。