数据结构与算法学习五（基于JavaScript）----堆

数据集合有序，能够为各种操作带来便利。但有些应用并不要求所有数据都是有序的，或者在操作开始之前就变的完全有序。
一些应用需要先收集一部分数据，从中选出最大或最小的关键码记录，后序收集更多的数据但始终处理数据中最小或最大关键码的记录，比如优先级队列， 优先级队列并不满足先进先出的特性，他能做到高优先级的先出队列，在优先级队列的各种实现中，堆是最高效的一种数据结构。堆是一种完全二叉树。

1 概念

• 1.1 关键码
  假定在数据记录中存在一个能够标识数据记录的数据项，并可依据该数据项对数据进行组织，则称此数据项为关键码(key)。
  关键码的作用就是比较大小的。
• 1.2 最小堆
  父节点的关键码小于等于左右子节点的关键码。即所有父节点都小于子节点。
• 1.3 最大堆
  父节点的关键码大于等于左右子节点的关键码。

最小堆的特性

数组的索引从0 开始，元素个数为n,在堆中给定索引为i的节点时(n即为数组的长度，i是下标)：

• 如果i=0，节点i是根节点，否则节点i的父节点为（i-1）/2 。
• 如果2i+1>n-1,则节点i无左子女节点，否则节点i的左子女节点为2i+1;
• 如果2i+2>n-1,则节点i无右子女节点，否则节点i的右子女节点为2i+2;

先定义一个数组：

var min_heap_arr = [9,17,65,23,45,78,87,53,31];

以上面的数组为例。 初始化后的一颗完全二叉树

注意：上图并不是一个最小堆。

我们需要将其调整为一个最小堆。

调整的过程自下而上，先保证局部是一个最小堆，然后从局部到整体，逐步扩大，知道整颗树调整为最小堆。

算法：

• 找到所有的分支节点，然后根据这些分支节点的索引从大到小依次调整，每次调整时，从该分支节点向下进行调整，使得这个分支节点和它的子孙节点构成一个最小堆。

• 假设数组的大小为n，则最后一个分支节点的索引是(n-2)/2,第一个分支节点的索引是0。如上图最后一个分支节点是9（索引是3）.

• 在局部进行调整时，如果父节点的关键码小于等于子女中的最小的关键码，说明不需要调整，否则将父节点和拥有最小关键码的子女进行位置互换，并继续向下比较调整。

调整过程如下：

• 第一步：进行调节的分支节点索引为3（最后一个分支节点）。
  
• 第二步：进行调整的节点索引为2.
  
  调整后的结构：
  
• 第三步：进行调整的分支节点索引为1.
  
  调整后的结构：
  
• 第四步：进行调整的分支节点索引为0.
  
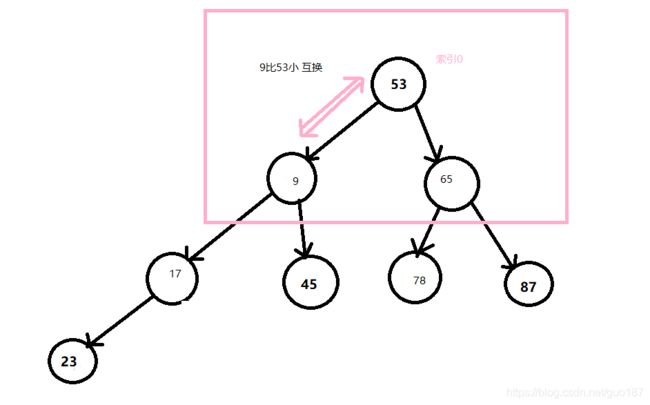
  调整后的结构：
  
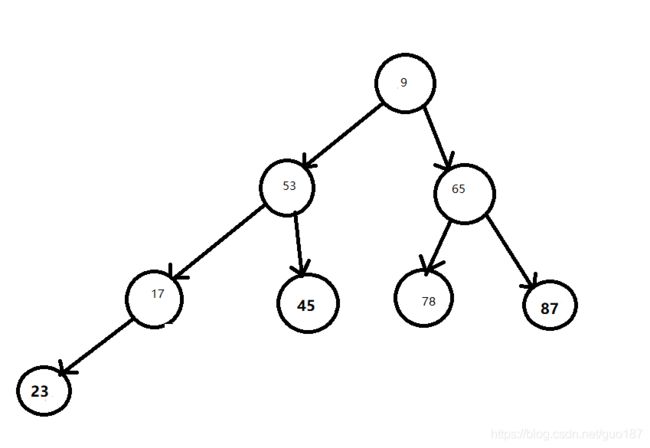
  调整后53比17大 继续调整
  
  调整后53比23大 继续调整
  
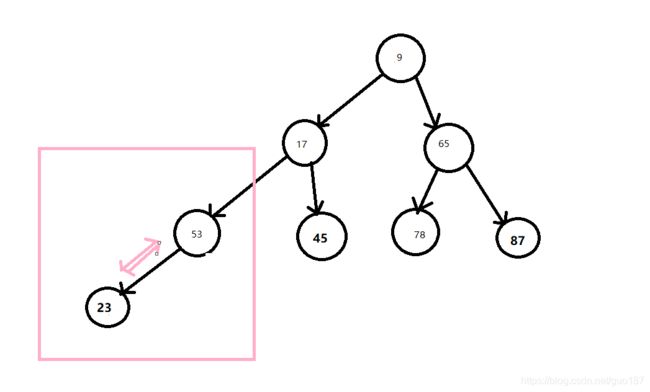
  调整完后，一个最小堆就出来啦。
  
  实例代码

//传入一个数组
function MinHeap(arr){
    var heap = new Array(arr.length);
    var curr_size = arr.length;//当前堆的大小
    var max_size = curr_size;//堆的最大容量
    var shif_down = function (start,m){
        let parent_index = start;//从start位置开始 向下下滑调整
        let min_child_index = parent_index*2 + 1;//最后一个分支节点的左子树 一定存在
        while(min_child_index<=m){
            //min_child_index 是左子树的索引  左子树的值大于右子树的值
            if(min_child_indexheap[min_child_index+1]){
                min_child_index = min_child_index + 1;//min_child_index永远指向值小的
            }
            //如果父节点的值小于等于两个子节点的最小值
            if(heap[parent_index]<=heap[min_child_index]){
                break;//循环结束 不需调整
            }else{
                //父节点和子节点的值互换
                var temp = heap[parent_index];
                heap[parent_index] = heap[min_child_index];
                heap[min_child_index] = temp;
                parent_index = min_child_index;
                min_child_index = 2*min_child_index+1;
            }
        }
    }
 
    this.init = function(){
      //填充heap
      for (let i = 0; i < arr.length; i++) {
        heap[i]=arr[i];
      }
      var  curr_pos = Math.floor((curr_size-2)/2);//堆的最后一个分支节点
      while(curr_pos>=0){
          shif_down(curr_pos,curr_size-1);//局部自上而下下滑调整
          curr_pos -= 1;//调整下一个分支节点
      }
    //   console.log(heap);//[ 9, 17, 65, 23, 45, 78, 87, 53 ]
    }

    var shif_up = function(start){
        var child_index = start;//当前节点是叶节点
        var parent_index = Math.floor((child_index-1)/2);//找到父节点

        while(child_index>0){
            if(heap[parent_index]<=heap[child_index]){//父节点更小 不用调整
                break;
            }else{
                //父节点和子节点值互换
                var temp  = heap[child_index];
                heap[child_index] = heap[parent_index];
                heap[parent_index] = temp;
                child_index = parent_index;
                parent_index = Math.floor((parent_index-1)/2);
            }
        }

    }
    //插入 注意插入时要考虑堆的容量 否则会插入失败的
    this.insert = function(item){
        if(curr_size == max_size){//堆满了 不能再放元素了
            return false;
        }
        heap[curr_size] = item;
        shif_up(curr_size);
        curr_size++;
        return true;
    }
    //删除最小堆的最小值，用后一个元素取代堆顶元素，取代后，最小堆被破坏，使用shif_down方法做向下调整
    this.remove_min = function(){
        if(curr_size<=0){
            return null;
        }
        var min_value = heap[0];
        heap[0] = heap[curr_size-1];
        curr_size--;
        shif_down(0,curr_size-1);
        return min_value;
    }
    //打印最小堆
    this.print = function(){
        console.log(heap);
    }
    //返回堆的大小
    this.size = function(){
        return curr_size;
    }
    //返回最小堆的堆顶 即最小值
    this.get_min = function(){
        if(curr_size>0){
            return heap[0];
        }
        return null;
    }
}

var arr = [53,17,78,9,45,65,87,23];//初始化
var test = new MinHeap(arr);
test.init();
// test.insert(11);
// test.print();
// console.log(test.size());
// console.log(test.get_min());
// console.log(test.remove_min());//9

insert 方法的实现思路

将新的元素插入到最小堆，由于此前，最小堆已经建好，那么就可以从下向上，与父节点的值比较，对调。

如插入11，11在最后一个位置，

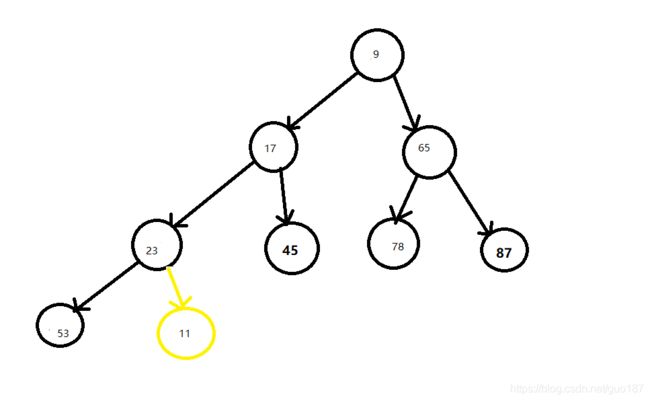
和父节点23相比 比23小 需要互换位置

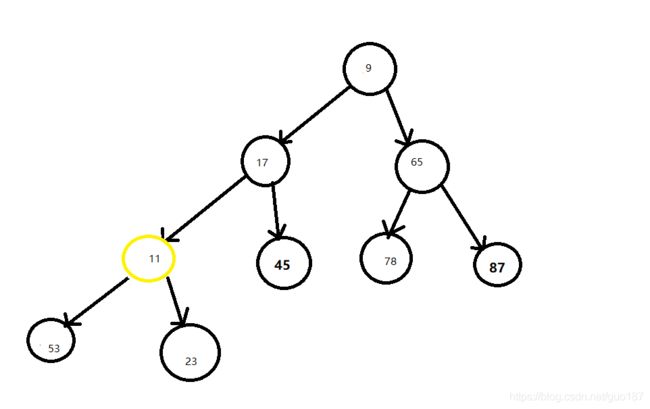
调整后11比17小 需要互换位置，调整后

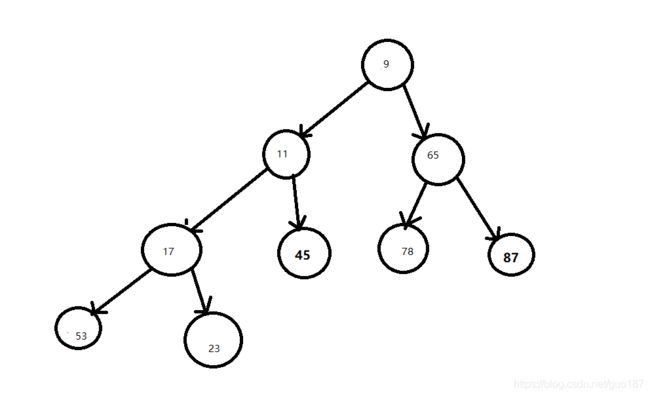
最小堆的应用

1、排序
使用最小堆进行排序，使用待排序数组初始化最小堆，然后追个删除堆顶元素，由于堆顶元素始终最小，所以可以得到一个有序的数组。

var arr01 = [53,17,78,9,45,65,87,23];
var min_heap = new MinHeap(arr01);
min_heap.init();
// min_heap.print();
var sort_arr = [];
for (let i = 0; i < arr01.length; i++) {
    sort_arr.push(min_heap.remove_min());   
}
console.log(sort_arr);//[ 9, 17, 23, 45, 53, 65, 78, 87 ]

2、Top K 问题
一个非常大的数据集合有n个整数，求集合中最大的K个值。
思路：初始化一个大小为K的最小堆，先放入K个数，这时，堆顶元素最小，
集合中剩余的数依次和堆顶元素比较，如果比堆顶元素大，则删除堆顶元素，并放入新元素。
全部比较完以后，堆里的元素就是最大的K个值。

var arr02 = [53,17,78,9,45,65,87,23];
var min_heap01 = new MinHeap([53,17,78]);
min_heap01.init();

for (let i = 3; i < arr02.length; i++) {
    var item = arr02[i];
    if(item >min_heap01.get_min()){
        min_heap01.remove_min();
        min_heap01.insert(item);
    }
}

min_heap01.print();//[ 65, 78, 87 ]