利用图神经网络进行的知识图谱补全综述
A Survey on Graph Neural Networks for Knowledge Graph Completion-论文阅读笔记
- 前言
- 数据集
- 基本概念
-
- 信息传递神经网络
- 图卷积网络(GCN)
- 图注意力网络(GATs)
- 解码器(Decoder)
- GCN Encoder用于图谱补全
- SACN( Relation Weighted GCN Encoder)
- Graph Attention Encoder(图注意力编码器)
- Standalone GNN for KBC
- Incorporating rules with GNN(规则和GNN的结合)
-
- 马尔可夫网
- MLN with GNN for inference
- 总结
作者:Siddhant Arora
单位:Indian Institute of Technology Delhi
联系方式:[email protected]
论文地址: 论文下载
前言
最近在看图谱补全相关的内容,现在比较多的方向是采用图嵌入的方式进行学习,这篇论文综述了图神经网络在补全上的应用,值得读一读。
主要要解决的问题是 ( e 1 , r , ? ) (e_1,r,?) (e1,r,?)这样的预测任务。之前的诸如transE,transH都采用使用的加法模型,关系是实体之间的表达。之后提出了乘法模型Distmult,Complex等。这些模型都是翻译模型。后来提出了旋转模型(Rotate),认为头实体可以通过旋转匹配到尾实体.
如今更多的神经网络模型用于图谱(ConvE,ConvKB)介绍了得分函数和模型一起被训练,但是这些方法都是将三元组孤立了,忽略了丰富的邻居节点的语义信息。
于是图神经网络的特性,其可以捕捉到邻居节点的信息,有很多研究聚焦于这用于图谱补全。
数据集
- FB15k,这是关系数据集FreeBase的子集,广泛用于图谱补全测试,数据集测试集由逆三元组组成 ( e 1 , r − 1 , e 2 ) (e_1,r{-}1,e_2) (e1,r−1,e2),其中 ( e 2 , r , e 1 ) (e_2,r,e_1) (e2,r,e1)在训练集中。所以一些简单的模型可以在训练集中可以得到很高的精度,所以又提出了FB15k-237移除了逆三元组。
- WN18,是wordNet KB(包含了单词间的词汇关系)的子集,和FB15k类似,也存在逆三元组,所以提出了WN18RR,WN18RR有层级结构导致对所有不处理传递关系的补全模型都提出了很大的挑战。
补全的评测标准主要是分为两种:
- MNN, Mean Reciprocal Rank该指标针对给定查询测量正确结果e2的倒数排名的平均值,
- Hits@R,它衡量e2在排名列表的前N个中出现的次数。
基本概念
信息传递神经网络
这是一个17年提出的框架,旨在推广为基于图数据提出的各种神经网络。对顶点 v v v的嵌入 n v n_v nv,两个顶点 v v v, w w w的边的嵌入为 e v w e_{vw} evw,首先定义信息函数。
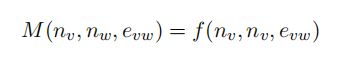
f(·)是非线性函数,从所有的邻居节点 w w w的信息聚合函数被定义为图下
![]()
其中 N ( v ) N(v) N(v)是节点 v v v的所有邻居集合,t是聚合时间戳,AGG是聚合函数(可以是sum,mean)等,最后节点 v v v通过更新函数UPD被更新。
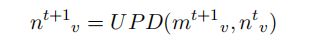
图卷积网络(GCN)
图卷据网络是基于谱神经网络的,这里贴一个我看到一个博主写的GCN,较为详细知乎,如何理解GCN
每个数据集是由顶点集,邻接矩阵和特征集组册灰姑娘的。这些特征可以是分类属性,节点标签,结构特征等等。GCNs使用如下函数聚合邻居节点信息
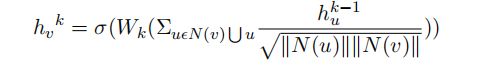
图注意力网络(GATs)
在GCNs中所有邻居都是同等贡献,同样这也有注意力机制,使用不同的权重来衡量不同的节点聚合信息。

GATs可以推广到不可见的节点,从而模拟现实世界,在各种任务中有STOA的成绩。
GATs的输入层是节点特征,N是节点数量。
![]()
每条边的注意力权重是的计算公式如下图
![]()
其中 W W W是权重矩阵, a a a是任一注意力函数, e i j e_{ij} eij是节点 i i i, j j j直接的边的注意力权重。对于每个节点 i i i,使用softmax函数进行权重归一化。每个节点的输出嵌入又下式定义
解码器(Decoder)
很多的的图谱补全方法都利用GNN作为编码器来得到相邻关系三元组的信息。诸如DistMult已经存在的得分函数会初始化他的实体嵌入来丰富信息,这样比单纯使用得分函数的方法结果好。这样的得分函数称为解码器。
GCN Encoder用于图谱补全
R-GCN引入了一个局部敏感的嵌入,然后传入decoder来预测图谱中丢失的连接。需要强调的是简单的额GCN由于忽略了边的标签无法用于图嵌入。因此R-GCN修改得分函数来捕捉边的关系

R是关系的集合, N v r N_v^r Nvr是和顶点v和关系r相连的实体集合。此模型为关系设置了新的权重。他们使用偏置和块对角分解来解决无法应对大规模知识图谱问题。在偏置分解中,每个关系的权重矩阵被表示为基础矩阵的和,在块对角分解中,每个关系权重矩阵被表示为块对角矩阵的直接和。这些方法可以防止过拟合但是让每个权重矩阵都互相依赖。从而帮助更好地将从频繁发生的关系中学到的知识转移到学习权重矩阵中,以获得更好的稀有关系。
本文的方法不研究节点邻域的差分称重,也不需要解码器,因为他们不学习通过GNN框架嵌入关系。
SACN( Relation Weighted GCN Encoder)
通过对关系的边缘敏感,从节点领域聚合信息。这被称之为加权图卷积网络(WGCN),将整个图分为子图,每个子图只含有一种类型的关系边。GCN通过下式应用于每个子图中。
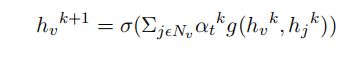
其中 h v k + 1 h_v^k+1 hvk+1是节点 v v v在k+1层的嵌入, N v N_v Nv是关系类型t指定的节点v的领域。g(·)就是一个简单的矩阵乘法,连接系数矩阵W是所有关系共享的。
之后利用可学习参数 α t \alpha_t αt对子图进行信息加权聚合.和R-GCN类似,SACN使用WGCN做ecoder,用Conv-TransE做解码器。而且没有改变关系和实体的形状,所以可以保持嵌入的翻译属性。还有个贡献就是这个方法使用了节点属性增强了节点嵌入,就是通过节点的关系属性添加为通过关系连接的两个实体之间的桥梁节点。
在FB15k和WN18NN数据集上取得了STOA的成绩。
Graph Attention Encoder(图注意力编码器)
上述两种方法都有处理节点关系时都采用了同等权重,KB-GAT使用注意力机制来分辨邻居节点信息的重要度。使用GNN作为编码器,使用例如ConvKB的神经网路得分函数做解码器。不同的是,他们使用GNNs来一起学习实体和关系的嵌入,对于每个三元组,他们表示了图的关系边,计算使用了下述式子
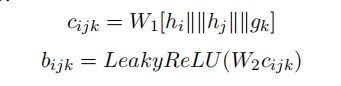
其中 h i , h j h_i,h_j hi,hj是实体嵌入, g k g_k gk是关系嵌入,这些嵌入式通过加法的TransE模型初始化。之后这些嵌入被concate并被乘以学习的权重矩阵 W i , W j W_i,W_j Wi,Wj,之后使用softmax函数对所有边到目标节点 i i i的权重矩阵进行计算,为每条边生成注意力权重。

Standalone GNN for KBC
TransGCN是一个GCN框架联合实体和关系嵌入,所以没有使用解码器。该方法排除了任务特定解码器的需要,并避免了在编码器步骤和解码器步骤中以关系嵌入的形式对关系进行二次学习的计算成本,它的目的是利用关系嵌入来转换图中节点的现有实体嵌入,使其成为齐次图。定义了两种转换运算。.和*。 t = h . r , h = t ∗ r t=h.r,h=t*r t=h.r,h=t∗r,当是入度边的时候 t = h . r t=h.r t=h.r,出度的时候使用另一个。
Incorporating rules with GNN(规则和GNN的结合)
马尔可夫网
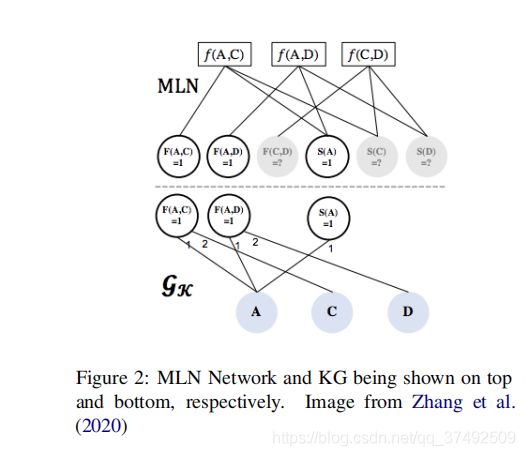
马尔可夫逻辑网络作为一阶逻辑和概率图模型的交集,将每个知识库=图谱表示为 ( F , w ) (F,w) (F,w),其中F是公式集,w是分配给每个公式的权重。马尔可夫网络是由知识图谱构造的,它通过在一边生成一个具有公式的二部图,在另一边生成它们的接地实例 (ground instance)。然后利用下面给出的方程对马尔可夫网络进行推理
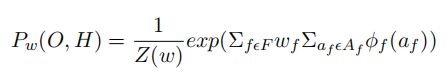
O O O是已被标记的事实, H H H是未被标记的事实, A f A_f Af是grounded predictate, ϕ f \phi_f ϕf是聚合函数定义了grounded predicates的真实值, Z ( w ) Z(w) Z(w)是正则因子。
MLN with GNN for inference
从上个公式可以得出 Z ( w ) Z(w) Z(w)需要指数级别的计算,所谓有人提出了ExpressGNN,他们用GNN使计算易于处理。首先将图谱表示为二部图,其中一边是实体,另一边是边。通过最大化已观察得到的事实的似然函数来优化,称之为 P w ( O , H ) P_w(O,H) Pw(O,H)。为此,他们计算了后验概率 Q θ ( H ∣ Q ) Q_{\theta}(H|Q) Qθ(H∣Q),未知三元组通过GNN从已知的三元组中聚合信息、他们通过EM算法来优化该过程。
总结
还有GNN的可解释性这个不想写了!大家自己看把。再看下实验结果
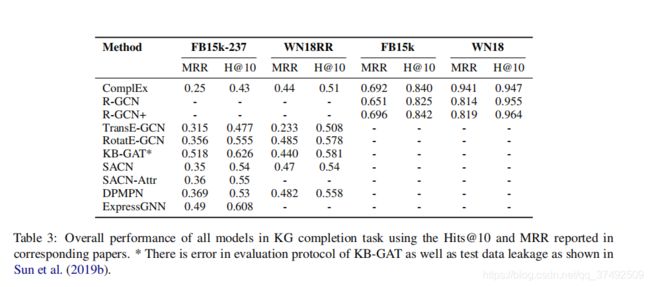
可以看出GNN广泛提高了知识图谱补全的STOA性能,这一成功不仅仅局限于链路预测任务,还有其他任务依旧在研究中。此外,所有的知识图完成方法都提出了一个固有的假设,即测试三元组中的所有实体都在训练时间中可以被看到,但这个假设可能不适用于实际场景。
另外我们从下图可以看出没有一个单一的方法拥有所有的优点。Express GNN和DPMPN网络似乎不能完全处理图中的异构性。最后很多方法在WN18RR上表现不好,可能是因为这些基于GNN的方法都没有有效的处理层级关系。有学者提出将知识图谱投影到双曲空间中。未来的工作可能聚焦于此。!