一、定义
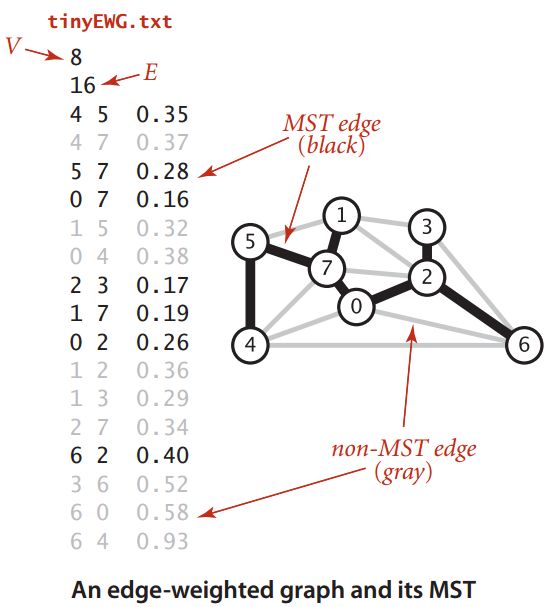
最小生成树(Minimum Spanning Tree,MST)仅针对加权连通无向图。对于一副加权连通无向图,其生成树是它的一棵含有其所有顶点的无环连通子图。
最小生成树(MST)是指它的一棵权值最小的生成树。
API定义:
二、性质
最小生成树的两种主要算法(Prim算法和Kruskal算法)都基于切分定理。
最小生成树具有以下性质:
- 具体V个顶点的加权连通无向图,其最小生成树包含V个顶点,V-1条边。
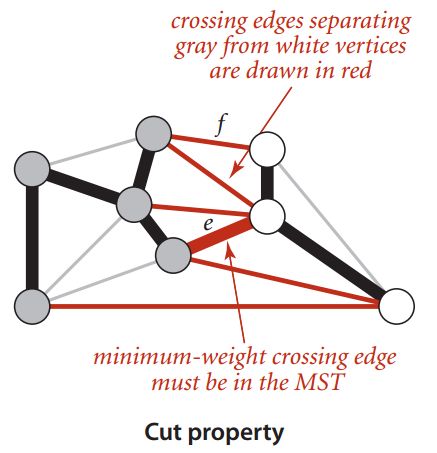
- 切分定理
在一副加权连通无向图G中,将所有顶点分成两个非空不相交子集U和V,假设顶点u∈U、v∈V,则对于权值最小的边e=(u,v),该图的最小生成树一定包含e。
证明(反证法):
假设T是图G的最小生成树,且T不包含e=(u,v)。
①根据树的定义,T中必然存在一条路径f(假设f≠e),连接U和V(因为树中所有顶点必然是连通的);
②将e加入树T,p和e必然构成一个回路(树中加入任意一条边都会构成回路)
③去掉回路中比e大的边,将生成比原T权重更小的生成树T'(与原假设中T是最小生成树矛盾)
三、Prim算法实现
3.1 基本思想
Prim算法是为一棵生长中的树添加边,每次添加一条。
初始时,这棵树只有一个顶点,然后添加V-1条边,每次总是选择到树中任意顶点最短的边添加。
具体步骤:
- 将图中所有顶点分属两个集合U和V:
U:树顶点(已被选入生成树的顶点)
V:非树顶点(还未被选入生成树的顶点) - 选择任意一个顶点加入U
- 枚举U,找到U到V之间的一条最短路径,将这条最短路径对应的非树顶点加入树顶点。
- 重复步骤3(共V-1次),直到所有顶点加入树顶点。
3.2 源码实现
public class LazyPrimMST {
private double weight; // total weight of MST
private Queue mst; // edges in the MST
private boolean[] marked; // marked[v] = true if v on tree
private MinPQ pq; // edges with one endpoint in tree
public LazyPrimMST(EdgeWeightedGraph G) {
mst = new Queue();
pq = new MinPQ();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++) // run Prim from all vertices to
if (!marked[v]) prim(G, v); // get a minimum spanning forest
}
private void prim(EdgeWeightedGraph G, int s) {
scan(G, s);
while (!pq.isEmpty()) { // better to stop when mst has V-1 edges
Edge e = pq.delMin(); // smallest edge on pq
int v = e.either(), w = e.other(v); // two endpoints
if (marked[v] && marked[w]) continue; // lazy, both v and w already scanned
mst.enqueue(e); // add e to MST
weight += e.weight();
if (!marked[v]) scan(G, v); // v becomes part of tree
if (!marked[w]) scan(G, w); // w becomes part of tree
}
}
// add all edges e incident to v onto pq if the other endpoint has not yet been scanned
private void scan(EdgeWeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v))
if (!marked[e.other(v)]) pq.insert(e);
}
public Iterable edges() {
return mst;
}
public double weight() {
return weight;
}
public static void main(String[] args) {
In in = new In(args[0]);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
LazyPrimMST mst = new LazyPrimMST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
StdOut.printf("%.5f\n", mst.weight());
}
}
3.3 算法优化
3.2 中对的Prim算法可以采用索引优先队列优化:
用索引优先队列保存各个非树顶点到树顶点集合的最短距离;一个distTo数组保存非树顶点v到树顶点集合的最短距离,初始时为正无穷大。
优化版本源码:
public class PrimMST {
// edgeTo保存最小生成树的边
private Edge[] edgeTo;
// distTo[v]表示非树顶点v到树顶点集合的最短距离,初始时为正无穷大
private double[] distTo;
private boolean[] marked;
// 索引优先队列,保存各个非树顶点到树顶点集合的最短距离
private IndexMinPQ pq;
public PrimMST(EdgeWeightedGraph G) {
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
pq = new IndexMinPQ(G.V());
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
// run from each vertex to find minimum spanning forest
for (int v = 0; v < G.V(); v++)
if (!marked[v])
prim(G, v);
}
// run Prim's algorithm in graph G, starting from vertex s
private void prim(EdgeWeightedGraph G, int s) {
distTo[s] = 0.0;
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin(); // 找到一条最短切边对应的顶点v
marked[v] = true; // 加入树顶点集合
//对顶点v的邻边进行处理
for (Edge e : G.adj(v)) {
int w = e.other(v);
if (marked[w])
continue;
if (e.weight() < distTo[w]) { // 更新w到树顶点集合的最短距离
distTo[w] = e.weight();
edgeTo[w] = e;
if (pq.contains(w))
pq.decreaseKey(w, distTo[w]);
else
pq.insert(w, distTo[w]);
}
}
}
}
public Iterable edges() {
Queue mst = new Queue();
for (int v = 0; v < edgeTo.length; v++) {
Edge e = edgeTo[v];
if (e != null) {
mst.enqueue(e);
}
}
return mst;
}
public double weight() {
double weight = 0.0;
for (Edge e : edges())
weight += e.weight();
return weight;
}
public static void main(String[] args) {
In in = new In(args[0]);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
PrimMST mst = new PrimMST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
StdOut.printf("%.5f\n", mst.weight());
}
}
3.4 性能分析
Prim算法的时间复杂度一般为O(ElgV),采用索引优先队列优化后可以达到O(ElgE)。
四、Kruskal算法实现
4.1 基本思想
Kruskal算法的基本步骤如下:
- 首先按边的权值从小到达排序;
- 每次从剩余边中选出权值最小的,且顶点未连通的两个顶点,加入到生成树中;
- 直到加入V-1条边为止。
4.2 源码实现
public class KruskalMST {
private static final double FLOATING_POINT_EPSILON = 1E-12;
private double weight; // weight of MST
private Queue mst = new Queue(); // edges in MST
public KruskalMST(EdgeWeightedGraph G) {
// more efficient to build heap by passing array of edges
MinPQ pq = new MinPQ();
for (Edge e : G.edges()) {
pq.insert(e);
}
// run greedy algorithm
UF uf = new UF(G.V());
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
Edge e = pq.delMin();
int v = e.either();
int w = e.other(v);
if (!uf.connected(v, w)) { // v-w does not create a cycle
uf.union(v, w); // merge v and w components
mst.enqueue(e); // add edge e to mst
weight += e.weight();
}
}
// check optimality conditions
assert check(G);
}
/**
* Returns the edges in a minimum spanning tree (or forest).
* @return the edges in a minimum spanning tree (or forest) as
* an iterable of edges
*/
public Iterable edges() {
return mst;
}
/**
* Returns the sum of the edge weights in a minimum spanning tree (or forest).
* @return the sum of the edge weights in a minimum spanning tree (or forest)
*/
public double weight() {
return weight;
}
// check optimality conditions (takes time proportional to E V lg* V)
private boolean check(EdgeWeightedGraph G) {
// check total weight
double total = 0.0;
for (Edge e : edges()) {
total += e.weight();
}
if (Math.abs(total - weight()) > FLOATING_POINT_EPSILON) {
System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", total, weight());
return false;
}
// check that it is acyclic
UF uf = new UF(G.V());
for (Edge e : edges()) {
int v = e.either(), w = e.other(v);
if (uf.connected(v, w)) {
System.err.println("Not a forest");
return false;
}
uf.union(v, w);
}
// check that it is a spanning forest
for (Edge e : G.edges()) {
int v = e.either(), w = e.other(v);
if (!uf.connected(v, w)) {
System.err.println("Not a spanning forest");
return false;
}
}
// check that it is a minimal spanning forest (cut optimality conditions)
for (Edge e : edges()) {
// all edges in MST except e
uf = new UF(G.V());
for (Edge f : mst) {
int x = f.either(), y = f.other(x);
if (f != e) uf.union(x, y);
}
// check that e is min weight edge in crossing cut
for (Edge f : G.edges()) {
int x = f.either(), y = f.other(x);
if (!uf.connected(x, y)) {
if (f.weight() < e.weight()) {
System.err.println("Edge " + f + " violates cut optimality conditions");
return false;
}
}
}
}
return true;
}
/**
* Unit tests the {@code KruskalMST} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
In in = new In(args[0]);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
KruskalMST mst = new KruskalMST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
StdOut.printf("%.5f\n", mst.weight());
}
}
4.3 性能分析
Kruskal算法一般还是比Prim算法慢,因为在处理每条边时,除了两种算法都要完成的优先队列操作外,Kruskal算法还需要进行一次并查集的connect()操作。