函数依赖

函数依赖

定义

设R(U)是属性集U上的关系模式，X,Y是U的子集。若对于R（U）的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等而在Y上的属性值不相等，则称X函数确定Y或Y函数依赖于X ，记作X->Y,X称为决定因素，即唯一的X确定唯一的Y

如果X->Y且Y->X,则记作 X<–>Y

分类

1. 非平凡的函数依赖 ： Y并不是X的子集
2. 平凡的函数依赖 ： Y是X的子集（任意关系必然成立）自己决定自己

完全函数依赖与部分函数依赖

如果X->Y,且X的真子集不函数决定Y，则称为Y对X完全函数依赖，否则称为部分函数依赖

如：(Sno,Cno)->Sdept,如果Sno->Sdept,则为部分函数依赖

传递依赖

Y非平凡函数依赖于X，X非平凡函数依赖于Y，则X->Z

范式

第一范式

所有属性满足原子性，即所有属性都不可再分，如果某元素需要被解析来获得目标信息，则认为是不符合原子性的，如一长串不同的电话号码

第二范式

R属于第一范式，并且每一个非主属性完全函数依赖于任何一个候选码

即任何候选码都可以唯一确定所有的非主属性元素

第三范式

在第二范式的基础上，每一个非主属性既不传递依赖于码，也不部分依赖与码

所有的非主属性对码都应该是直接完全函数依赖

BCNF范式

BCNF范式是第三范式的修正，如果每一个决定因素都含有码，则符合BCNF范式

逻辑蕴涵

对于满足一组函数依赖F的关系模式R,其任何一个关系r，若函数依赖X->Y都成立，则称F逻辑蕴涵X->Y

阿姆斯特朗公理

1. 自反律 ： 若Y是X的子集，X是U的子集，则X->Y为F所蕴含
2. 增广律 ： 若X->Y为F所蕴含，且Z是U的子集，则XZ->YZ为F所蕴含
3. 传递律 ： 若X->Y及Y->Z为F所蕴含，则X->Z为F所蕴含

阿姆斯特朗推理规则

• 合并规则 ： 有X->Y,X->Z，有X->YZ
• 伪传递规则 ： 有X->Y,WY->Z,有XW->Z
• 分解规则 ： 有X->Y及Z是Y的子集，有X->Z

闭包

设F为属性集U上的一组函数依赖，X，Y是U的子集，X_f ={A|X->A能由F根据阿姆斯特朗公理导出}，X_f⁺称为属性集X关于函数依赖集F的闭包

即 属性X在函数依赖集合F下，能够决定的所有属性的集合

闭包计算（属性闭包方式）

例如 ： 求 属性集AG关于F的闭包

(闭包还可以使用 阿姆斯特朗公理求解，但较为复杂，通常使用属性闭包法)

函数依赖F闭包

若F为关系模式R(U)的函数依赖集，我们把F以及所有被F逻辑蕴涵的函数依赖的集合称为F的闭包，记为F+。

函数依赖集F的闭包，里面的元素还是函数依赖（就是X→Y这种东西），函数依赖集F的闭包包括F自身，加上能从F中通过Armstong公理推导出的，新的函数依赖。

闭包的作用

• 判断是不是superkey
• 计算F的闭包

最小正则覆盖

判断是否是冗余函数依赖

去掉可以通过推导简介得出的依赖函数，例如

在RHS中 ： A->CD 可以分解为 A—>C，A——>D ,A——>C可以由A——>B和B——>C得到，因此只需要A——>D即可

最小正则覆盖拥有最小的函数依赖集，没有冗余的函数依赖和属性

判断是否是冗余属性

1. 要判断的属性位于依赖的左侧，例如{AB→C}，则删除该属性，在原本的依赖集F中计算该依赖左部集合的闭包α+。若α+闭包中包含该依赖右侧所有的属性，则该属性则是无关属性
   例：函数依赖集F{Z→X，X→P，XY→WP，XYP→ZW}
   关注到XYP中的P属性。它在左侧。删除它，求解左侧剩下属性集XY的闭包，求取域是原来的F{Z→X，X→P，XY→WP，XYP→ZW}。因为XY→WP，所以（XY）+ = XYWP；又因为XYP→ZW，所以（XY）+ = XYWPZ，包含依赖右侧ZW
   故P是无关属性

2. 若要判断的属性位于依赖的右侧，例如{AB→C，……}，则删除该属性，在余下的函数依赖集F’中计算该依赖左部集合的闭包α+。若α+中包含要判断的属性，则该属性就是无关属性（冗余）

   例：F{A→BC，B→AC，C→AB}
   关注B属性。它在依赖右侧。删除该属性，余下F’={A→C，B→AC，C→AB},计算左侧剩余属性集（A）的闭包（A）+。
   因为A→C，C→AB，所以（A）+中包含删去的属性B
   故B是无关属性

最小正则覆盖计算

1.在函数依赖集F中使用联合律替代原有的函数依赖，如

​ A->B1 , A->B2 替换为 A->B1B2

2.在F中发现冗余的函数依赖和属性，删去

例如：

基于函数依赖的算法

模式分解与规范化

无损连接分解

当一个关系模式R分解为R₁、R₂……R_n的时候，如果R₁……R_n能够通过自然连接合为R，则称该分解为无损分解

如何判断无损分解

1. 简单分解判断（分解为两个子集A、B）

   A∩B ——> A-B

   A、B的交集 决定 A、B的差集

2. 通用判断

   1. 画表
   2. 填充符号a
   3. 根据函数依赖填充表
   4. 循环步骤3
   5. 如果有一行是满符号a的，则是无损连接的，反之就不是

   例子

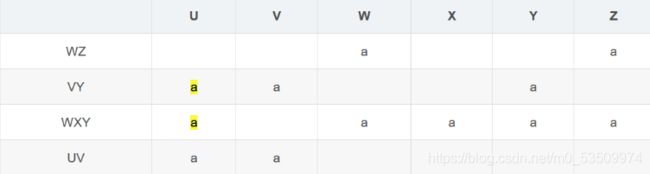
   关系模式R（U，V，W，X，Y，Z），函数依赖F={U→V，W→Z，Y→U，WY→X}，分解ρ={WZ，VY，WXY，UV}

   1.画表

2.填充符号a

根据表ρ中的元素，在表格跟ρ属性相关的一格，填充为a

如 ：子集WZ 含有元素 W、Z ， 则 第一行W、Z为a

3.根据函数依赖填充表

U→V : 第四行 V 为 a

W→Z ： 第一行、第三行 的 Z 为a

Y→U ： 第二行、第三行的 U 为a

WY→X ： 第三行的 X 为a

4.循环第三步

U→V : 此时第二、第三、第四行都有了U ， 则 第二、第三、第四行的V 都变为 a

5.如果有一行是满符号a的，则是无损连接的，反之就不是
显然第三行WXY为满符号a ， 则说明该分解是无损分解。

依赖保持

依赖保持的定义

R₁ …… R_n 的函数依赖的并集的闭包 = R的函数依赖F的闭包

依赖保持的充分条件

R的所有依赖函数在R₁……R_n 中都存在R_k能够成立，则是依赖保持的（只需要有子集能够成立即可）

判断某个依赖保持算法（通过属性闭包的形式）

显然B->A、D->A、A->E、AC->B中除了D->A外在R₁中都存在，因此只需要判断D->A即可

基于函数依赖的BCFN分解

判定某关系模式方法

检查依赖集F中所有的函数依赖是否都遵守BCFN范式

判断分解之后的关系模式是否是BCFN范式

使用原R的函数依赖集的闭包的所有函数依赖来判断分解之后的R_i

AC->D ∈ F⁺ 因此需要用闭包来判断

BCFN分解算法

1. 令p={R}
2. 如果p中的模式不属于BCNF，把该模式的函数依赖集合F中，决定因素不含有候选码的依赖组成一个模式S1，其他依赖组成一个模式S2放入p中，此时S2为BC范式，因为S2中每一个决定决定因素都含有候选码，。然后把S1，S2替换掉R。
3. 重复第二步，直到所有的模式都符合BCNF。

例如 ：

B->C不满足BC范式==（B不是码）==，因此用B——>C把R分开，在新的R₁中B成为了码

例 : R（A,B,C,D,E,F,G）

​ F (A—>B、A—>C 、C—>D 、C—>E 、E—>FG) 候选码 ： A

1. ρ = R
2. 不含有候选码的 R1 = (C,D,E,F,G) 其他含有候选码的R2(A,B,C)
3. ρ = {R1,R2} 对于R1 , R3 = (C,D,E) R4 = (E,F,G)
4. ρ = {R1,R2,R3,R4}

多值依赖(MVDs)

定义

设R（U）是属性集U上的一个关系模式，X,Y,Z是U的子集，并且Z=U-X-Y。关系模式中多值依赖X->->Y成立，当且仅当对R（U）的任一关系r，给定的一对（x,z）值，有一组Y的值，这组值仅仅决定于x值而与z值无关

判断多值依赖的方法

即某关系模式R中， 同时有元组** ,**

每一个函数依赖都是多值依赖

多值依赖与第四范式

第四范式分解

判断每一个函数依赖是否符合第四范式（是否有多值依赖），如果不满足，就分解

第四范式

限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖

根据函数依赖求解 候选码

1. 将R中所有属性分为 UL = {只存在于依赖左边的属性}

   UR = {只存在于依赖右边的属性}

   UB = {两边都存在的属性}

2. UL 中的属性必定属于某个候选码

   UR 中的属性必定不属于候选码

3. 求取UL的闭包UL⁺ ,如果闭包 = R ，则UL 为候选码

4. 如果UL闭包！=R ，则将UB 中的元素逐个添加入UL 求取闭包，直到求出U为止，对应为候选码