matlab中复高斯分布_利用GPML-V4.1工具箱实现高斯过程回归(GPR)的多变量数据预测...
本帖最后由 iqiukp 于 2019-9-5 11:55 编辑
2019.9.5 更新
![]()
2019-9-5 11:53 上传
点击文件名下载附件
使用方法:在MATLAB中把文件夹切换到demo_1或者demo_2所在的根目录,直接运行demo_1.m或者demo_2.m即可。
%{
x : training inputs
y : training targets
xt: testing inputs
yt: testing targets
%}复制代码按照以上的变量说明,把实验数据替换为自己的数据。
说明:
1. 把GPML工具箱替换为V4.2版本
2. 增加了demo(多输入单输出demo和多输入多输出demo)
3. 增加了一些必要的说明
3.1.用feval(@函数名字)可以查看函数的超参数个数,比如:
K>> feval(@covRQiso)
ans =
'(1+1+1)'复制代码说明协方差函数covRQiso需要3个超参数,因此利用minimize函数优化covRQiso超参数的时候需要初始化为3个数。每个超参数的含义以及取值范围在每个函数的说明里面都有详细介绍。
3.2. 不同的似然函数有着不同的推理函数要求,具体可以看./doc/index.html或者./doc/manual.pdf
3.3. GPML工具箱也可以应用于(单)多输入单输出的回归,工具箱提供的demo也是单输入单输出的。数据格式需要设定为“行方向为样本方向,列方向为变量方向”。
3.4. 回归精度与似然函数、推理函数以及协方差函数的选择均有关;优化超参数的迭代次数也是一个重要的影响因素。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
demo1: 多输入单输出例子
%%%%%%%%%% Gaussian Process Regression (GPR) %%%%%%%%%
% Demo: prediction using GPR
% ---------------------------------------------------------------------%
clc
close all
clear all
addpath(genpath(pwd))
% load data
%{
x : training inputs
y : training targets
xt: testing inputs
yt: testing targets
%}
% 多输入单输出例子
load('./data/data_1.mat')
% 设定均值函数、协方差函数以及似然函数
% 以meanConst、covRQiso和likGauss为例
meanfunc = @meanConst;
covfunc = @covRQiso;
likfunc = @likGauss;
% 超参数初始化
hyp = struct('mean', 3, 'cov', [0 0 0], 'lik', -1);
% 设定均值函数、协方差函数以及似然函数
% 以covSEiso和likGauss为例
% meanfunc = [];
% covfunc = @covSEiso;
% likfunc = @likGauss;
% % 超参数初始化
% hyp = struct('mean', [], 'cov', [0 0], 'lik', -1);
% 优化超参数
hyp2 = minimize(hyp, @gp, -20, @infGaussLik, meanfunc, covfunc, likfunc,x, y);
% 利用优化后的超参数进行GPR建模
% yfit为预测值的均值,ys为预测值的方差
[yfit ys] = gp(hyp2, @infGaussLik, meanfunc, covfunc, likfunc,x, y, xt);
% 可视化结果
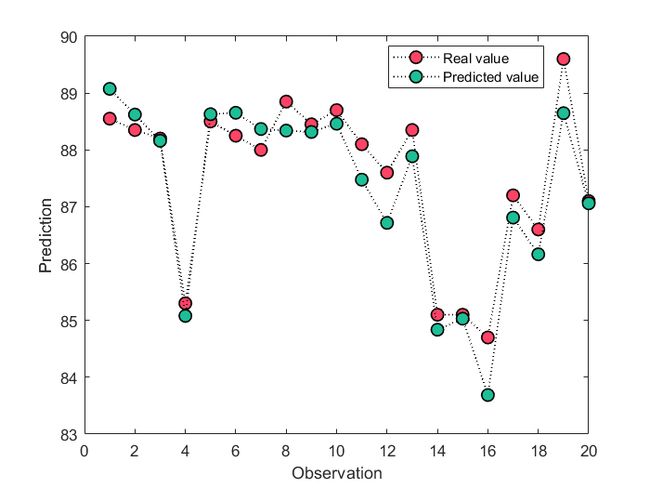
plotResult(yt, yfit)复制代码结果:
demo_1_1.png (33.6 KB, 下载次数: 21)
2019-9-5 11:48 上传
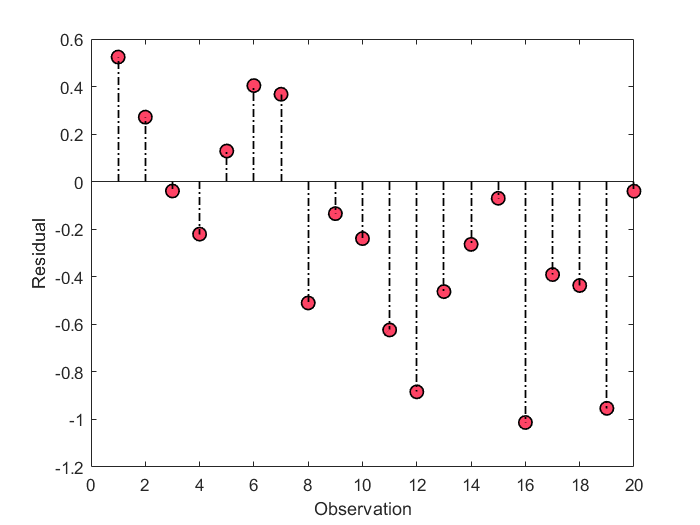
demo_1_2.png (22.63 KB, 下载次数: 25)
2019-9-5 11:48 上传
demo2: 多输入多输出例子
%%%%%%%%%% Gaussian Process Regression (GPR) %%%%%%%%%
% Demo: prediction using GPR
% ---------------------------------------------------------------------%
clc
close all
clear all
addpath(genpath(pwd))
% load data
%{
x : training inputs
y : training targets
xt: testing inputs
yt: testing targets
%}
% 多输入单输出例子
load('./data/data_2.mat')
% 设定均值函数、协方差函数以及似然函数
% 以meanConst、covRQiso和likGauss为例
meanfunc = @meanConst;
covfunc = @covRQiso;
likfunc = @likGauss;
% 超参数初始化
hyp = struct('mean', 3, 'cov', [2 2 2], 'lik', -1);
% 设定均值函数、协方差函数以及似然函数
% 以covSEiso和likGauss为例
% meanfunc = [];
% covfunc = @covSEiso;
% likfunc = @likGauss;
% % 超参数初始化
% hyp = struct('mean', [], 'cov', [0 0], 'lik', -1);
% 优化超参数
hyp2 = minimize(hyp, @gp, -5, @infGaussLik, meanfunc, covfunc, likfunc,x, y);
% 利用优化后的超参数进行GPR建模
% yfit为预测值的均值,ys为预测值的方差
[yfit ys] = gp(hyp2, @infGaussLik, meanfunc, covfunc, likfunc,x, y, xt);
% 可视化结果
% 第一个输出
plotResult(yt(:,1), yfit(:,1))
% 第二个输出
plotResult(yt(:,2), yfit(:,2))复制代码
第一个输出的结果:
demo_2_1_1.png (36.88 KB, 下载次数: 16)
2019-9-5 11:48 上传
demo_2_1_2.png (26 KB, 下载次数: 36)
2019-9-5 11:48 上传
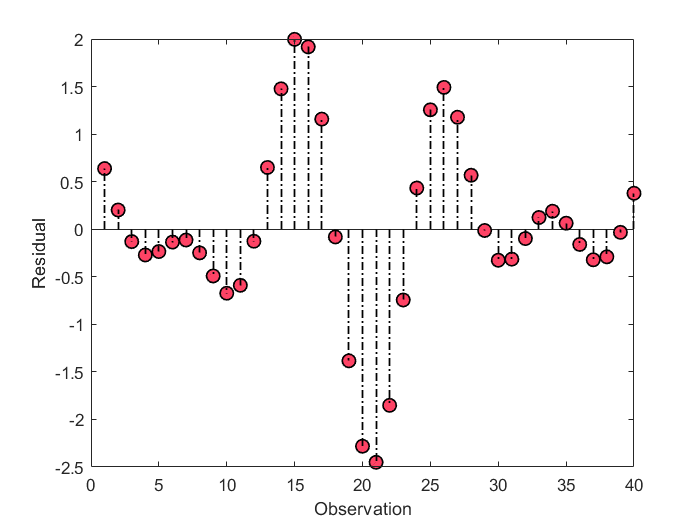
第二个输出的结果:
demo_2_2_1.png (34.87 KB, 下载次数: 23)
2019-9-5 11:48 上传
demo_2_2_2.png (24.16 KB, 下载次数: 25)
2019-9-5 11:48 上传