常用的三种线性模型算法--线性回归模型、岭回归模型、套索回归模型

常用的三种线性模型算法–线性回归模型、岭回归模型、套索回归模型

线性模型基本概念
线性模型的一般预测模型是下面这个样子的，一般有多个变量，也可以称为多个特征x1、x2、x3 …

最简单的线性模型就是一条直线直线的方程式，b0是截距，b1是斜率

比如说我们的画一条直线：y=0.5*x+3，他是最简单的线性模型

import numpy as np
import matplotlib.pyplot as plt 
#生成-5到5的元素数为100的数组
x=np.linspace(-5,5,100)
#输入直线方程
y=0.5*x+3
plt.plot(x,y,c='orange')
#图标题
plt.title('straight line')
plt.show()

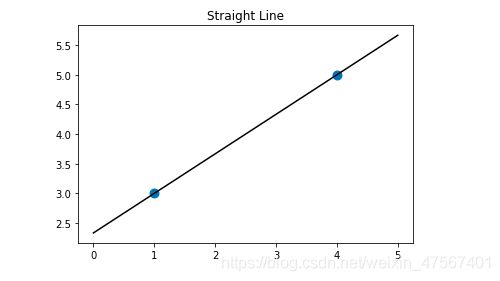
在初中的数学我们都知道是两点确定一条直线，比如说下面我们根据（1，3）、（4，5）来画出一条直线

import numpy as np
import matplotlib.pyplot as plt 
#导入线性回归模型
from sklearn.linear_model import LinearRegression 
#导入横纵坐标
X=[[1],[4]]
y=[3,5]
#线性拟合
lr=LinearRegression().fit(X,y)
#画图
z=np.linspace(0,5,20)
plt.scatter(X,y,s=80)
plt.plot(z,lr.predict(z.reshape(-1,1)),c='k')
plt.title('Straight Line')
plt.show()



print('\n\n\n 直线方程：')
print('=======\n')
print('y={:.3f}'.format(lr.coef_[0]),'x','+{:.3f}'.format(lr.intercept_))
print('=======\n')
print('\n\n\n')
 直线方程：
=======

y=0.667 x +2.333
=======

接下是三个点，我们多加一个点（3，3），你会看到当有多个点的时候直线没有办法穿过三个点，所以这个时候我们需要画出一条和三个点的距离和最小的直线

X=[[1],[4],[3]]
y=[3,5,3]
lr=LinearRegression().fit(X,y)
z=np.linspace(0,5,20)
plt.scatter(X,y,s=80)
plt.plot(z,lr.predict(z.reshape(-1,1)),c='k')
plt.title('Straight Line ')
plt.show()



print('\n\n\n 直线方程：')
print('=======\n')
print('y={:.3f}'.format(lr.coef_[0]),'x','+{:.3f}'.format(lr.intercept_))
print('=======\n')
print('\n\n\n')

 直线方程：
=======

y=0.571 x +2.143
=======

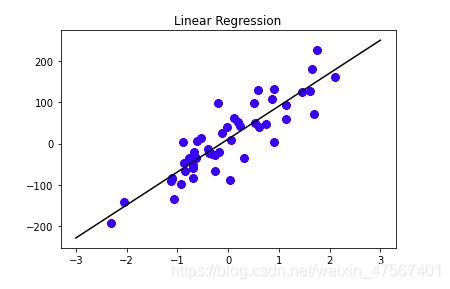
下面如果我们用scikit-learn来生成非常多的点，这个时候用python的库来绘制一条最优解的曲线就显得非常方便了

from sklearn.datasets import make_regression 
#用于生产回归分析数据
X,y=make_regression(n_samples=50,n_features=1,n_informative=1,noise=50,random_state=1)
#使用线性模型拟合
reg=LinearRegression()
reg.fit(X,y)
#生产等差数列用来画图
z=np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X,y,c='b',s=60)
plt.plot(z,reg.predict(z),c='k')
plt.title('Linear Regression')

print('\n\n\n 直线方程：')
print('=======\n')
print('y={:.3f}'.format(reg.coef_[0]),'x','+{:.3f}'.format(reg.intercept_))
print('=======\n')
print('\n\n\n')
 直线方程：
=======

y=79.525 x +10.922
=======

线性回归
线性回归的原理是找到训练数据集中的y和真实值的平方差最小。接下里我们还是用make_regression函数来生产多数据点。这里生成了100个，特征数量为2 的点

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression 
X,y=make_regression(n_samples=100,n_features=2,n_informative=2,random_state=38)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
lr=LinearRegression().fit(X_train,y_train)

print('\n\n\n ')
print('=======\n')
print("lr.coef_:{}".format(lr.coef_[:]))
print("lr.intercept_:{}".format(lr.intercept_))
print('=======\n')
print('\n\n\n')

#这里斜率存储在coef_中，截距储存在intercept_中
=======
lr.coef_:[70.38592453  7.43213621]
lr.intercept_:-1.4210854715202004e-14
=======

线性回归的表现，最高分是1.00

print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lr.score(X_train,y_train)))
print("test_score: {:.2f}".format(lr.score(X_test,y_test)))
print('=======\n')
print('\n\n\n') 


=======

 train_score: 1.00
test_score: 1.00
=======

这里我们换个数据，我们从数据库导入一个现实生活的数据，糖尿病的一些数据

from sklearn.datasets import load_diabetes
#导入真实数据集
X,y=load_diabetes().data,load_diabetes().target
#拆分成训练集和数据集
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
#用线性模型拟合
lr=LinearRegression().fit(X_train,y_train)

print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lr.score(X_train,y_train)))
print("test_score: {:.2f}".format(lr.score(X_test,y_test)))
print('=======\n')
print('\n\n\n') 

=======

 train_score: 0.53
test_score: 0.46
=======

岭回归-L2正规化线性模型
岭回归是一种可以避免过拟合的线性模型，在岭回归模型里面，会保存所有的特征变量，但是会减少特征变量的系数值。在回归模型中可以改变alpha的参数来控制减小特征变量系数的参数

from sklearn.linear_model import Ridge
ridge =Ridge().fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(ridge.score(X_train,y_train)))
print("test_score: {:.2f}".format(ridge.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')

=======

 train_score: 0.43
test_score: 0.43
=======

我们可以试着把alpha的大小改为10、0.1、1，来看下他们的打分。同时我们把图形画出来看下他们的差异

from sklearn.linear_model import Ridge
ridge10 =Ridge(alpha=10).fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(ridge10.score(X_train,y_train)))
print("test_score: {:.2f}".format(ridge10.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')


=======

 train_score: 0.15
test_score: 0.16
=======

from sklearn.linear_model import Ridge
ridge01 =Ridge(alpha=0.1).fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(ridge01.score(X_train,y_train)))
print("test_score: {:.2f}".format(ridge01.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')


=======

 train_score: 0.52
test_score: 0.47
=======

plt.plot(ridge.coef_,'s',label='Ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='Ridge alpha=10')
plt.plot(ridge01.coef_,'v',label='Ridge alpha=0.1')
plt.plot(lr.coef_,'o',label='linear regression')
plt.xlabel("coefficient index")
plt.ylabel("coefficient magnitude")
plt.hlines(0,0,len(lr.coef_))
plt.legend()!

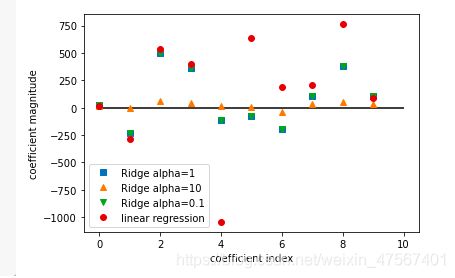
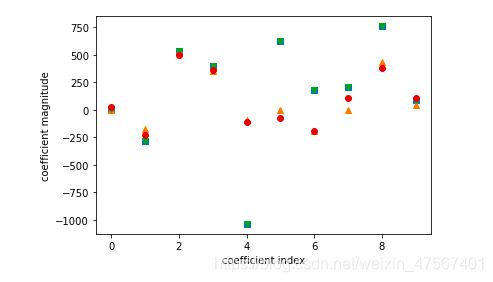
我们可以看出
alpha=10,特征变量的系数基本上为0附近
alpha=1特征变量的系数变大了
alpha=0.1特征变量的系数变得非常大了，几乎与线性回归的重合

from sklearn.model_selection import learning_curve,KFold
def plot_learning_curve(est,X,y):
    training_set_size,train_scores,test_scores=learning_curve(est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,random_state=1))
    estimator_name=est.__class__.__name__
    line=plt.plot(training_set_size,train_scores.mean(axis=1),'--',label="training"+estimator_name)
    plt.plot(training_set_size,test_scores.mean(axis=1),'-',label="test"+estimator_name,c=line[0].get_color())
    plt.xlabel('Training set size')
    plt.ylabel('Score')
    plt.ylim(0,1.1)
plot_learning_curve(Ridge(alpha=1),X,y)
plot_learning_curve(LinearRegression(),X,y)
plt.legend(loc=(0,1.05),ncol=2,fontsize=11)

我们也可以画出alpha为1的岭回归模型和线性回归莫模型

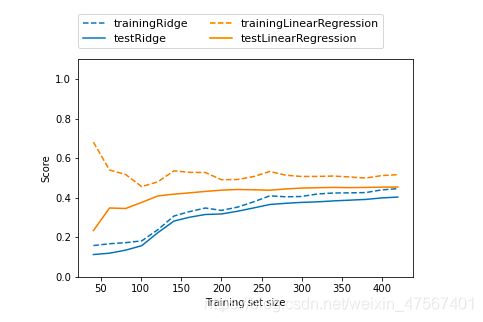
岭回归和线性回归主要的区别是正规化，在少数据的时候岭回归的打分在训练数据集的时候要低，但是在测试数据集都差不多。数据足够多两个模型没有太大差异，但是如果数据少的话一般是岭回归表现好。
套索回归-L1正规化的线性模型
和岭回归很想，套索回归会把系数限制在0附近，但是套索回归会让一部分数据的系数等于零，有助于让模型更容易理解

from sklearn.linear_model import Lasso
lasso=Lasso().fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lasso.score(X_train,y_train)))
print("test_score: {:.2f}".format(lasso.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')

=======

 train_score: 0.36
test_score: 0.37
=======

from sklearn.linear_model import Lasso
lasso01=Lasso(alpha=0.1,max_iter=100000).fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lasso.score(X_train,y_train)))
print("test_score: {:.2f}".format(lasso.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')

=======

 train_score: 0.53
test_score: 0.46
=======

from sklearn.linear_model import Lasso
lasso00001=Lasso(alpha=0.0001,max_iter=100000).fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lasso.score(X_train,y_train)))
print("test_score: {:.2f}".format(lasso.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')

=======

 train_score: 0.53
test_score: 0.46
=======

from sklearn.linear_model import Lasso
lasso011=Lasso(alpha=0.11,max_iter=100000).fit(X_train,y_train)
print('\n\n\n')
print('=======\n')
print(" train_score: {:.2f}".format(lasso.score(X_train,y_train)))
print("test_score: {:.2f}".format(lasso.score(X_test,y_test)))
print('=======\n')
print('\n\n\n')

=======

 train_score: 0.53
test_score: 0.46
=======

我们通过图像来了解一下

plt.plot(lasso.coef_,'s',label='Ridge alpha=1')
plt.plot(lasso011.coef_,'^',label='Ridge alpha=0.11')
plt.plot(lasso00001.coef_,'v',label='Ridge alpha=0.0001')
plt.plot(ridge01.coef_,'o',label='Ridge alpha=0.1')

plt.xlabel("coefficient index")
plt.ylabel("coefficient magnitude")

alpha=1，大部分系数为0
alpha=0.01，还是很多0，但少了不少
alpha=0.0001，这个时候很多点都不是零了。