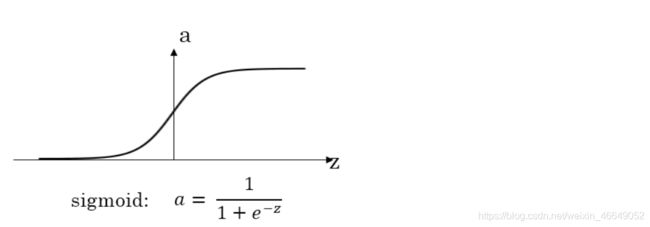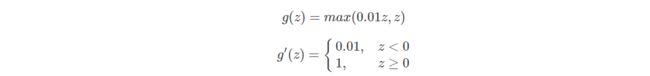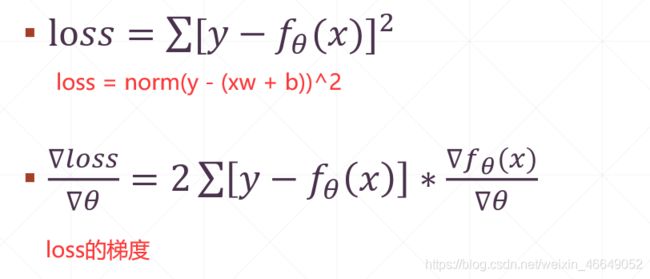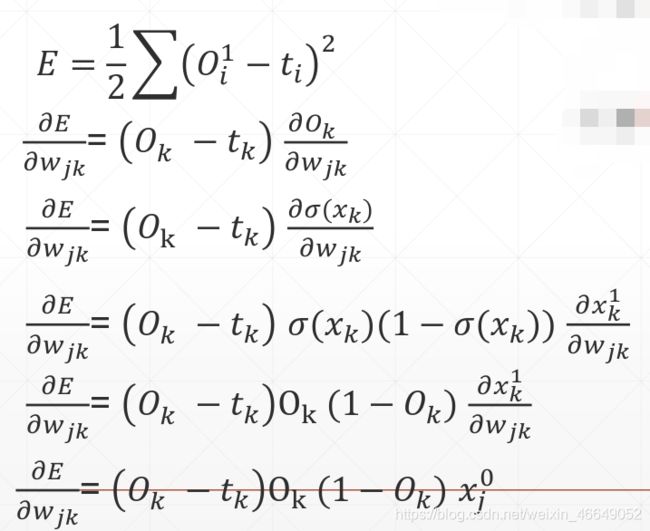深度学习TF—4.随机梯度下降
文章目录
-
-
- 一、梯度下降简介
-
- 1.梯度
- 2.如何搜索
- 3.利用tensorflow自动求解梯度并自动更新参数
- 4.案例—二阶导自定义
- 二、激活函数及梯度
-
- 1.sigmoid函数及其梯度
- 2.Tanh函数及其梯度
- 3.ReLU函数及其梯度
- 4.Leaky ReLU函数及其梯度
- 5.激活函数选择总结
- 三、损失函数及梯度
-
- 1.MSE—均方误差
- 2.交叉熵损失函数
- 四、感知机及梯度求解
-
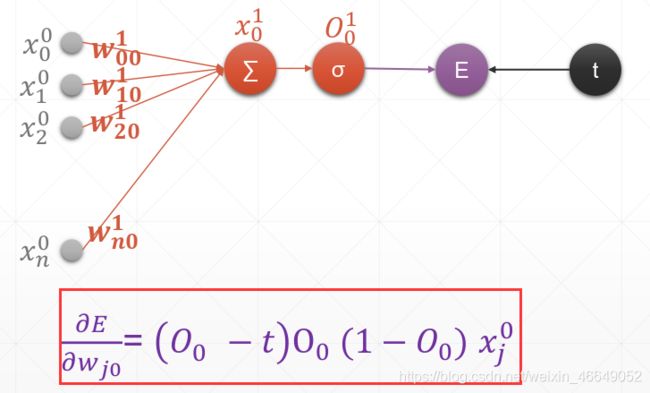
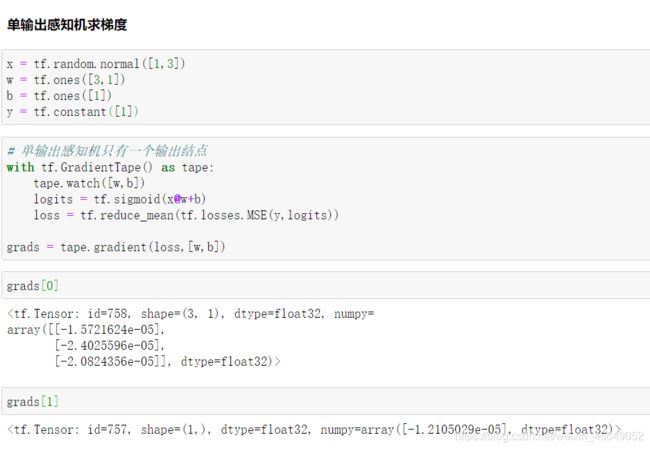
- 1.单输出感知机及梯度
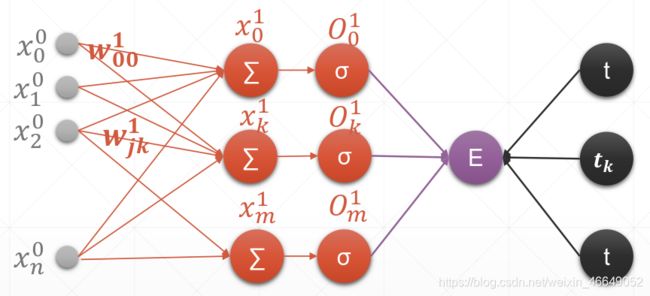
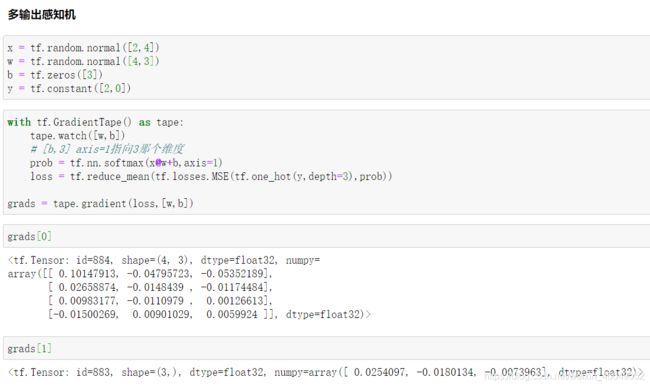
- 2.多输出感知机及梯度
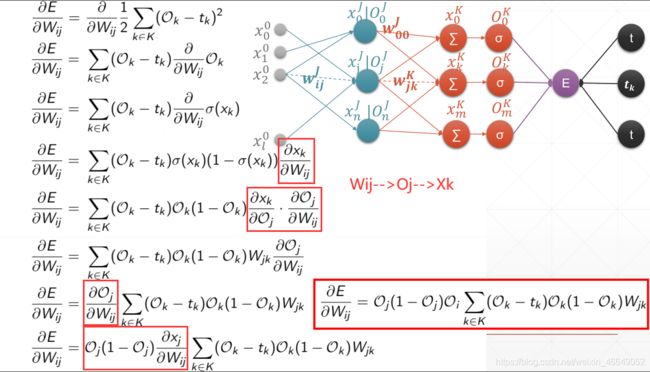
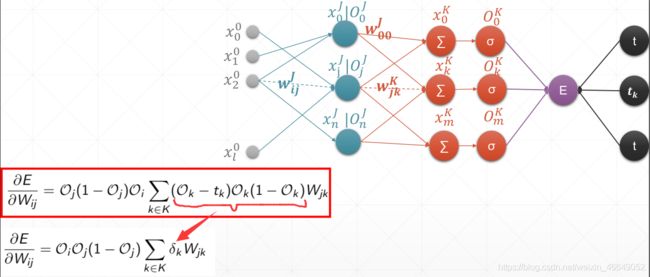
- 3.多层感知机及梯度
- 4.多层感知机案例
- 五、随机梯度下降实战
-
- 1.函数优化实战
- 2.手写数字问题实战
- 3.可视化实战—Tensorboard
-
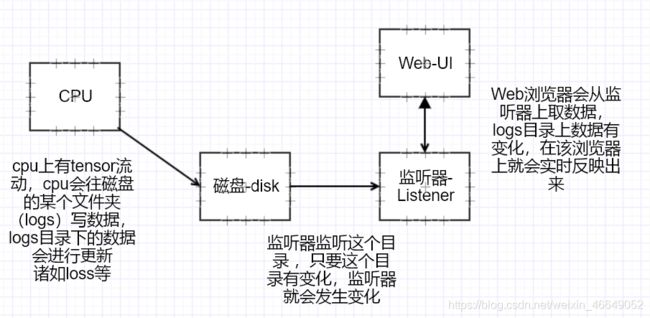
- 1.Tensorboard原理
- 2.如何可视化
- 3.案例
-
一、梯度下降简介
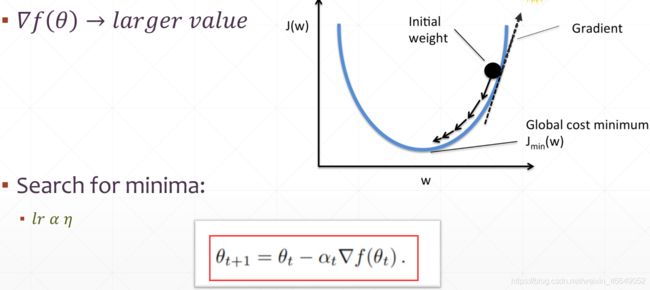
1.梯度
2.如何搜索
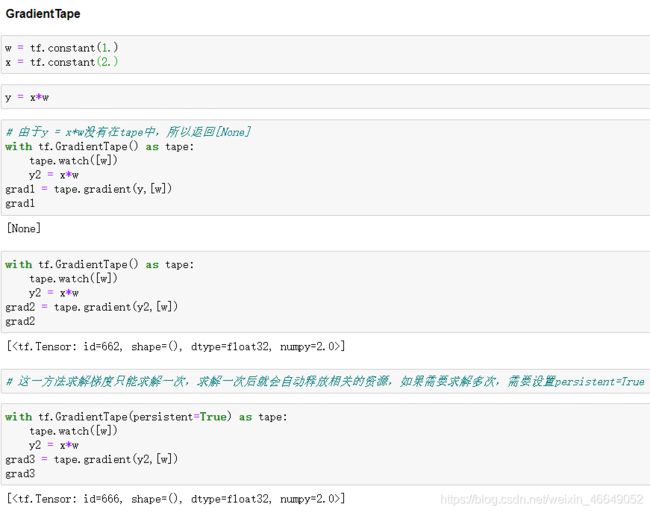
3.利用tensorflow自动求解梯度并自动更新参数
4.案例—二阶导自定义
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
w = tf.Variable(1.0)
b = tf.Variable(2.0)
x = tf.Variable(3.0)
with tf.GradientTape() as t1:
with tf.GradientTape() as t2:
y = x * w + b
dy_dw, dy_db = t2.gradient(y, [w, b])
d2y_dw2 = t1.gradient(dy_dw, w)
print(dy_dw)
print(dy_db)
print(d2y_dw2)
tf.Tensor(3.0, shape=(), dtype=float32)
tf.Tensor(1.0, shape=(), dtype=float32)
None
二、激活函数及梯度
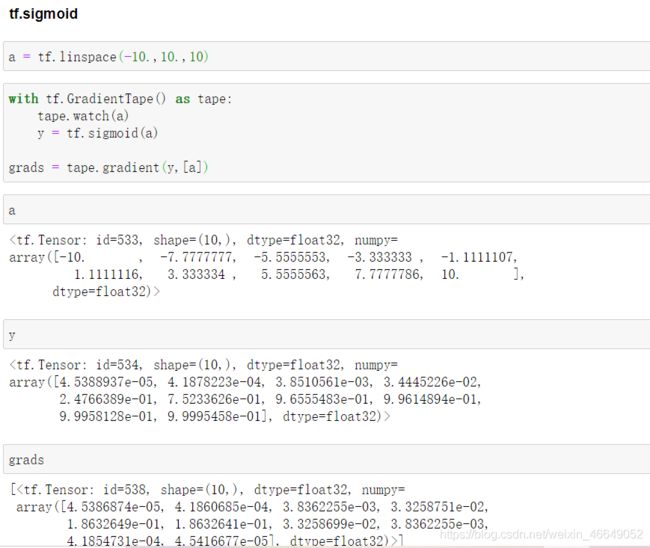
1.sigmoid函数及其梯度
该激活函数容易出现梯度离散,权值很长时间内未更新
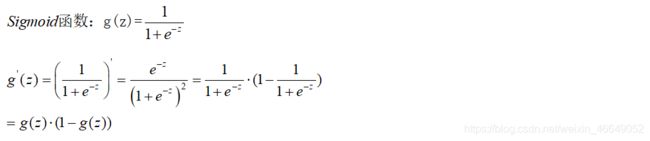
就是当|z|很大的时候,激活函数的斜率(梯度)很小。因此,在这个区域内,梯度下降算法会运行得比较慢。在实际应用中,应尽量避免使z落在这个区域,使|z|尽可能限定在零值附近,从而提高梯度下降算法运算速度。
2.Tanh函数及其梯度
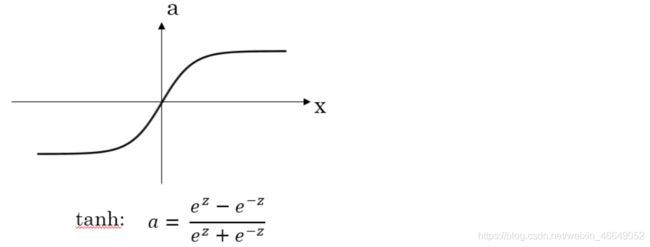
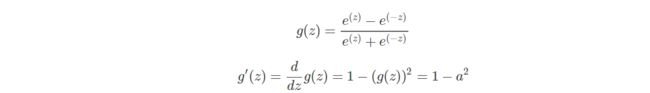
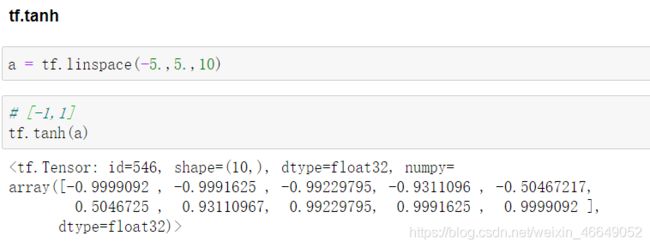
对于隐藏层的激活函数,一般来说,tanh函数要比sigmoid函数表现更好一些。因为tanh函数的取值范围在[-1,+1]之间,隐藏层的输出被限定在[-1,+1]之间,可以看成是在0值附近分布,均值为0。这样从隐藏层到输出层,数据起到了归一化(均值为0)的效果。因此,隐藏层的激活函数,tanh比sigmoid更好一些。
而对于输出层的激活函数,因为二分类问题的输出取值为{0,+1},所以一般会选择sigmoid作为激活函数。
观察sigmoid函数和tanh函数,我们发现有这样一个问题,就是当|z|很大的时候,激活函数的斜率(梯度)很小。因此,在这个区域内,梯度下降算法会运行得比较慢。在实际应用中,应尽量避免使z落在这个区域,使|z|尽可能限定在零值附近,从而提高梯度下降算法运算速度。
3.ReLU函数及其梯度

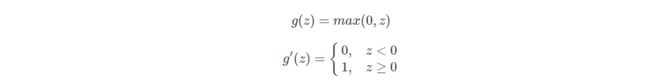
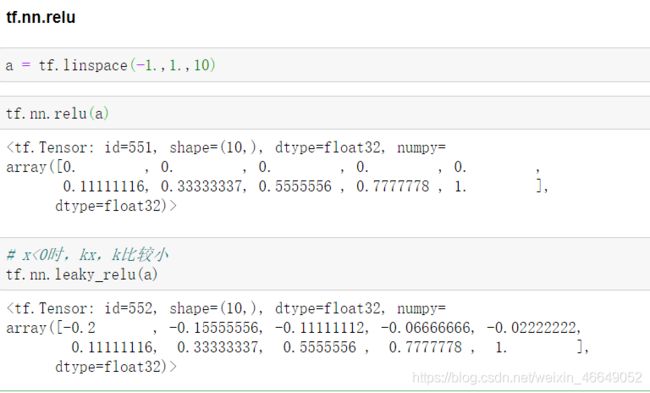
为了弥补sigmoid函数和tanh函数的这个缺陷,就出现了ReLU激活函数。ReLU激活函数在z大于零时梯度始终为1;在z小于零时梯度始终为0;z等于零时的梯度可以当成1也可以当成0,实际应用中并不影响。
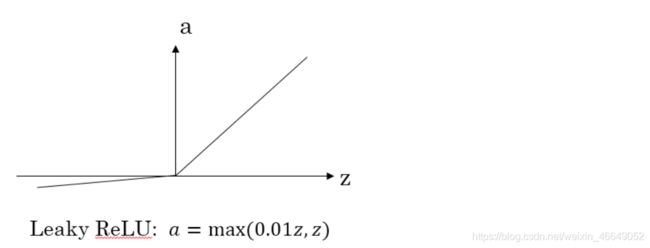
对于隐藏层,选择ReLU作为激活函数能够保证z大于零时梯度始终为1,从而提高神经网络梯度下降算法运算速度。但当z小于零时,存在梯度为0的缺点,实际应用中,这个缺点影响不是很大。为了弥补这个缺点,出现了Leaky ReLU激活函数,能够保证z小于零是梯度不为0。
4.Leaky ReLU函数及其梯度
5.激活函数选择总结
如果是分类问题,输出层的激活函数一般会选择sigmoid函数。
但是隐藏层的激活函数通常不会选择sigmoid函数,tanh函数的表现会比sigmoid函数好一些。实际应用中,通常会会选择使用ReLU或者Leaky ReLU函数,保证梯度下降速度不会太小。
其实,具体选择哪个函数作为激活函数没有一个固定的准确的答案,应该要根据具体实际问题进行验证(validation)。
三、损失函数及梯度
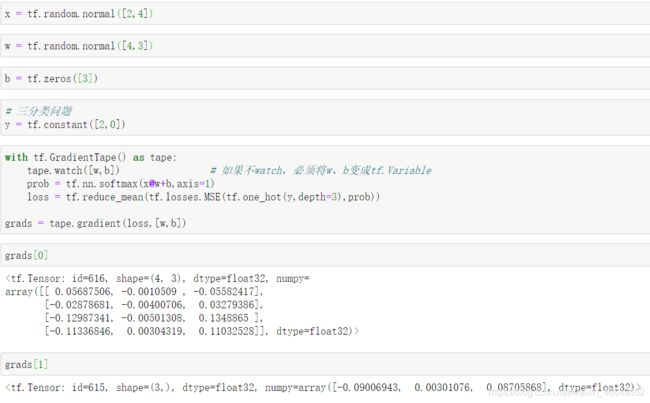
1.MSE—均方误差
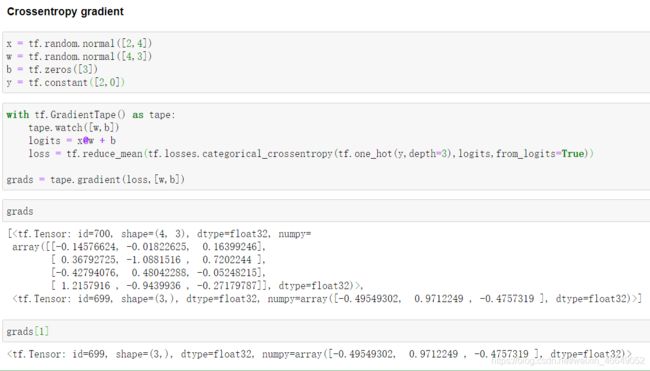
2.交叉熵损失函数
tf.losses.categorical_crossentropy

softmax函数求导


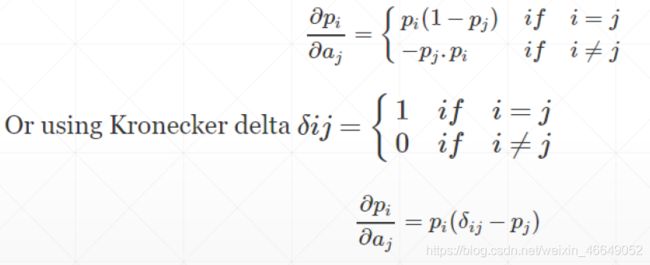
四、感知机及梯度求解
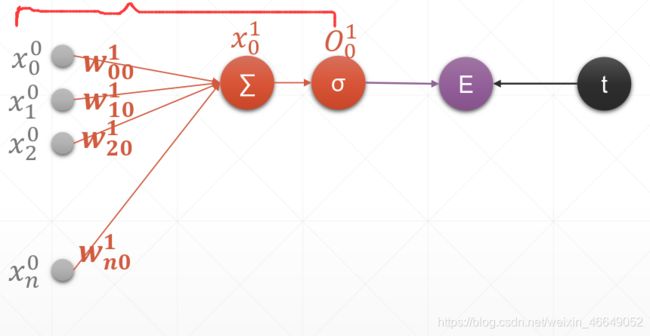
1.单输出感知机及梯度
2.多输出感知机及梯度
3.多层感知机及梯度
4.多层感知机案例
这里引用Kaggle里面简街市场预测的公开代码
from tensorflow.keras.layers import Input, Dense, BatchNormalization, Dropout, Concatenate, Lambda, GaussianNoise, Activation
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.losses import BinaryCrossentropy
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.layers.experimental.preprocessing import Normalization
import tensorflow as tf
import tensorflow_addons as tfa
import numpy as np
import pandas as pd
from tqdm import tqdm
from random import choices
SEED = 1111
np.random.seed(SEED)
train = pd.read_feather('../input/janestreetsaveasfeature/train.feather')
train = train.query('date > 85').reset_index(drop = True)
train = train[train['weight'] != 0]
train.fillna(train.mean(),inplace=True)
train['action'] = ((train['resp'].values) > 0).astype(int)
features = [c for c in train.columns if "feature" in c]
f_mean = np.mean(train[features[1:]].values,axis=0)
resp_cols = ['resp_1', 'resp_2', 'resp_3', 'resp', 'resp_4']
X_train = train.loc[:, train.columns.str.contains('feature')]
#y_train = (train.loc[:, 'action'])
y_train = np.stack([(train[c] > 0).astype('int') for c in resp_cols]).T
def create_mlp(
num_columns, num_labels, hidden_units, dropout_rates, label_smoothing, learning_rate
):
inp = tf.keras.layers.Input(shape=(num_columns,))
x = tf.keras.layers.BatchNormalization()(inp)
x = tf.keras.layers.Dropout(dropout_rates[0])(x)
for i in range(len(hidden_units)):
x = tf.keras.layers.Dense(hidden_units[i])(x)
x = tf.keras.layers.BatchNormalization()(x)
x = tf.keras.layers.Activation(tf.keras.activations.swish)(x)
x = tf.keras.layers.Dropout(dropout_rates[i + 1])(x)
x = tf.keras.layers.Dense(num_labels)(x)
out = tf.keras.layers.Activation("sigmoid")(x)
model = tf.keras.models.Model(inputs=inp, outputs=out)
model.compile(
optimizer=tfa.optimizers.RectifiedAdam(learning_rate=learning_rate), # 对于学习率的选择更具有鲁棒性
loss=tf.keras.losses.BinaryCrossentropy(label_smoothing=label_smoothing),
metrics=tf.keras.metrics.AUC(name="AUC"),
)
return model
epochs = 200
batch_size = 4096 # 批处理大小是2^x的倍数
hidden_units = [160, 160, 160]
dropout_rates = [0.2, 0.2, 0.2, 0.2]
label_smoothing = 1e-2
learning_rate = 1e-3
tf.keras.backend.clear_session()
tf.random.set_seed(SEED)
clf = create_mlp(
len(features), 5, hidden_units, dropout_rates, label_smoothing, learning_rate
)
clf.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=2)
# save model
clf.save(f'model.h5')
五、随机梯度下降实战
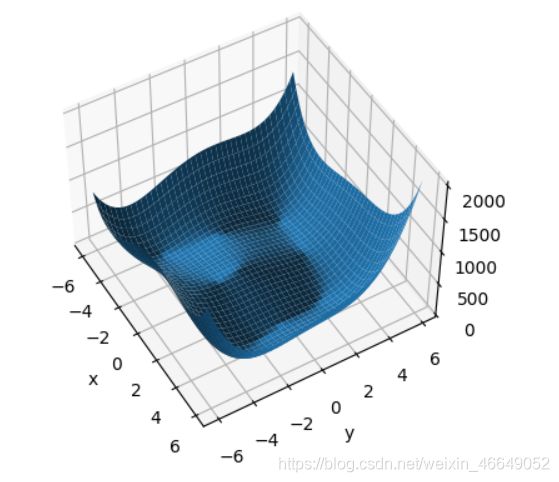
1.函数优化实战
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import tensorflow as tf
# 绘图
# 定义函数
def himmelblau(x):
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y)
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y])
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
# 梯度下降-优化
# [1., 0.], [-4, 0.], [4, 0.]
# 随机初始点-初始点不同,路径可能不同,局部最小值点可能改变
# x = tf.constant([4., 0.])
# x = tf.constant([1., 0.])
x = tf.constant([-4., 0.])
for step in range(200): # 迭代200次
with tf.GradientTape() as tape:
tape.watch([x]) # 如果构建x时,是tf.Variable类型则不需要这个操作
y = himmelblau(x)
grads = tape.gradient(y, [x])[0]
x -= 0.01*grads
if step % 20 == 0:
print ('step {}: x = {}, f(x) = {}'
.format(step, x.numpy(), y.numpy()))
x,y range: (120,) (120,)
X,Y maps: (120, 120) (120, 120)
step 0: x = [-2.98 -0.09999999], f(x) = 146.0
step 20: x = [-3.6890156 -3.1276684], f(x) = 6.054738998413086
step 40: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 60: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 80: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 100: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 120: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 140: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 160: x = [-3.7793102 -3.283186 ], f(x) = 0.0
step 180: x = [-3.7793102 -3.283186 ], f(x) = 0.0
2.手写数字问题实战
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
# 构造预处理函数
def preprocess(x, y):
x = tf.cast(x, dtype=tf.float32) / 255.
y = tf.cast(y, dtype=tf.int32)
return x, y
# x:[60k,28,28] x_test:[10k,28,28]
(x, y), (x_test, y_test) = datasets.fashion_mnist.load_data()
print(x.shape, y.shape)
print(x_test.shape, y_test.shape)
batchsz = 128
# 构造数据集
db = tf.data.Dataset.from_tensor_slices((x, y))
# 预处理,只需要传入函数而无需要传入函数的调用方式
db = db.map(preprocess).shuffle(10000).batch(batchsz)
db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
# 预处理,只需要传入函数而无需要传入函数的调用方式
db_test = db_test.map(preprocess).batch(batchsz)
db_iter = iter(db)
sample = next(db_iter)
print('batch:', sample[0].shape, sample[1].shape)
# 构建多层网络-最后一层一般不需要激活函数
model = Sequential([
layers.Dense(256, activation=tf.nn.relu), # [b,784] => [b,256]
layers.Dense(128, activation=tf.nn.relu), # [b,256] => [b,128]
layers.Dense(64, activation=tf.nn.relu), # [b,128] => [b,64]
layers.Dense(32, activation=tf.nn.relu), # [b,64] => [b,32]
layers.Dense(10), # [b,32] => [b,10] 330 = 32*10 + 10
])
# 构建输入维度
model.build(input_shape=[None, 28 * 28])
model.summary()
# 构建优化器
# 更新权值- w = w -lr*grad
optimizer = optimizers.Adam(lr=1e-3)
def main():
for epoch in range(30):
for step, (x, y) in enumerate(db):
# x[b,28,28] => x[b,784]
x = tf.reshape(x, [-1, 28 * 28])
with tf.GradientTape() as tape:
# 构建前向传播
# [b,784] => [b,10]
logits = model(x)
y = tf.one_hot(y, depth=10)
loss_mse = tf.reduce_mean(tf.losses.MSE(y, logits))
loss_ce = tf.losses.categorical_crossentropy(y, logits, from_logits=True)
loss_ce = tf.reduce_mean(loss_ce)
grads = tape.gradient(loss_ce, model.trainable_variables)
# 利用优化器统一原地更新
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss:', float(loss_ce), float(loss_mse))
# test
total_correct = 0
total_num = 0
for x, y in db_test:
x = tf.reshape(x, [-1, 28 * 28])
# [b,784] => [b,10]
logits = model(x)
prob = tf.nn.softmax(logits, axis=1)
# [b,10] => [b]
pred = tf.argmax(prob, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# pred:[b] y:[b]
correct = tf.equal(pred, y)
correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
# tensor => numpy
total_correct += int(correct)
total_num += x.shape[0]
acc = total_correct / total_num
print(epoch, 'test acc:', acc)
if __name__ == '__main__':
main()
(60000, 28, 28) (60000,)
(10000, 28, 28) (10000,)
batch: (128, 28, 28) (128,)
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 200960
_________________________________________________________________
dense_1 (Dense) multiple 32896
_________________________________________________________________
dense_2 (Dense) multiple 8256
_________________________________________________________________
dense_3 (Dense) multiple 2080
_________________________________________________________________
dense_4 (Dense) multiple 330
=================================================================
Total params: 244,522
Trainable params: 244,522
Non-trainable params: 0
_________________________________________________________________
0 0 loss: 2.303929090499878 0.242684006690979
0 100 loss: 0.5860539674758911 22.32927703857422
0 200 loss: 0.5546977519989014 27.239099502563477
0 300 loss: 0.3866368532180786 25.4809627532959
0 400 loss: 0.3865927457809448 28.153907775878906
0 test acc: 0.8482
1 0 loss: 0.4001665711402893 26.901527404785156
1 100 loss: 0.523040771484375 32.702239990234375
1 200 loss: 0.2962474822998047 37.23288345336914
1 300 loss: 0.5228046774864197 29.088302612304688
1 400 loss: 0.4941650331020355 31.387100219726562
1 test acc: 0.853
2 0 loss: 0.3662468492984772 31.163776397705078
2 100 loss: 0.2790403962135315 37.754085540771484
2 200 loss: 0.3591204583644867 36.052513122558594
2 300 loss: 0.30174970626831055 35.038909912109375
2 400 loss: 0.45119309425354004 33.016700744628906
2 test acc: 0.8629
3 0 loss: 0.3489121198654175 36.01388931274414
3 100 loss: 0.32831019163131714 46.060543060302734
3 200 loss: 0.22170956432819366 41.36198425292969
3 300 loss: 0.284996896982193 34.6197624206543
3 400 loss: 0.3549075722694397 48.20280838012695
3 test acc: 0.8682
...
29 0 loss: 0.1280389428138733 230.05148315429688
29 100 loss: 0.10448945313692093 262.2647705078125
29 200 loss: 0.11969716101884842 239.57110595703125
29 300 loss: 0.10605543851852417 246.7599639892578
29 400 loss: 0.09774138778448105 235.69046020507812
29 test acc: 0.8915
3.可视化实战—Tensorboard
1.Tensorboard原理
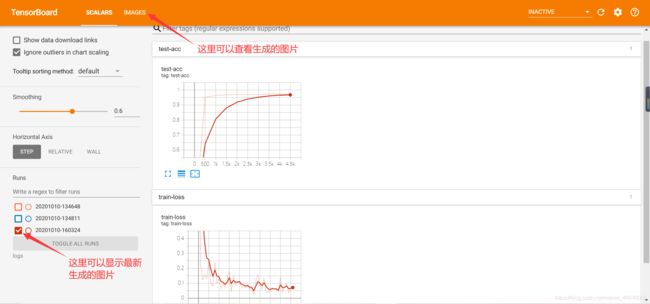
2.如何可视化
- Listen logdir logs
C:\Users\admin>dir
C:\Users\admin>cd Desktop
C:\Users\admin\Desktop>dir
C:\Users\admin\Desktop>cd 深度学习与TensorFlow入门实战-源码和PPT
C:\Users\admin\Desktop\深度学习与TensorFlow入门实战-源码和PPT>dir
C:\Users\admin\Desktop\深度学习与TensorFlow入门实战-源码和PPT>cd lesson28-可视化
C:\Users\admin\Desktop\深度学习与TensorFlow入门实战-源码和PPT\lesson28-可视化>tensorboard --logdir logs
2020-10-10 13:50:11.118488: I tensorflow/stream_executor/platform/default/dso_loader.cc:44] Successfully opened dynamic library cudart64_100.dll
Serving TensorBoard on localhost; to expose to the network, use a proxy or pass --bind_all
TensorBoard 2.0.2 at http://localhost:6006/ (Press CTRL+C to quit)
找到可视化网站,复制http://localhost:6006/到浏览器中即可
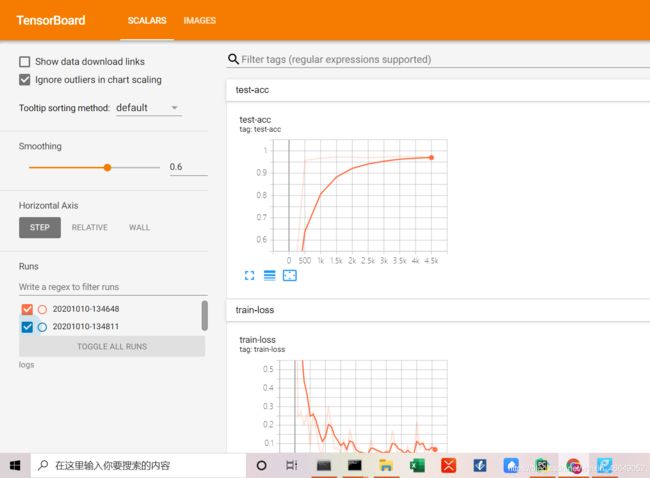
- bulid summary instance
current_time = datetime.datatime.now().strftime('%Y%m%d-$H%M%S')
log_dir = 'logs/ ' + current_time
summary_writer = tf.summary.create_file_writer(log_dir)# 数据更新
- fed data in summary instance
with summary_writer.as_default():
tf.summary.scalar('loss',float(loss),step=epoch)
tf.summary.scalar('accuracy',float(train_accuracy),step=epoch)
# 一张图片-fed single image
# get x from (x,y)
sample_img = next(iter(db))[0]
# get first image instance
sample_img = sample_img[0]
sample_img = tf.reshape(sample_img, [1, 28, 28, 1])
with summary_writer.as_default():
tf.summary.image("Training sample:", sample_img, step=0)
# fed multi-image
# print(x.shape)
val_images = x[:25]
val_images = tf.reshape(val_images, [-1, 28, 28, 1])
with summary_writer.as_default():
tf.summary.image("val-onebyone-images:", val_images, max_outputs=25, step=step)
val_images = tf.reshape(val_images, [-1, 28, 28])
figure = image_grid(val_images)
tf.summary.image('val-images:', plot_to_image(figure), step=step)
3.案例
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
import datetime
from matplotlib import pyplot as plt
import io
# 数据预处理
def preprocess(x, y):
x = tf.cast(x, dtype=tf.float32) / 255.
y = tf.cast(y, dtype=tf.int32)
return x, y
# 下面两个函数用来将多张图片拼成一张图片
def plot_to_image(figure):
"""Converts the matplotlib plot specified by 'figure' to a PNG image and
returns it. The supplied figure is closed and inaccessible after this call."""
# Save the plot to a PNG in memory.
buf = io.BytesIO()
plt.savefig(buf, format='png')
# Closing the figure prevents it from being displayed directly inside
# the notebook.
plt.close(figure)
buf.seek(0)
# Convert PNG buffer to TF image
image = tf.image.decode_png(buf.getvalue(), channels=4)
# Add the batch dimension
image = tf.expand_dims(image, 0)
return image
def image_grid(images):
"""Return a 5x5 grid of the MNIST images as a matplotlib figure."""
# Create a figure to contain the plot.
figure = plt.figure(figsize=(10, 10))
for i in range(25):
# Start next subplot.
plt.subplot(5, 5, i + 1, title='name')
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(images[i], cmap=plt.cm.binary)
return figure
batchsz = 128
(x, y), (x_val, y_val) = datasets.mnist.load_data()
print('datasets:', x.shape, y.shape, x.min(), x.max())
# 数据集加载并预处理
db = tf.data.Dataset.from_tensor_slices((x, y))
db = db.map(preprocess).shuffle(60000).batch(batchsz).repeat(10)
ds_val = tf.data.Dataset.from_tensor_slices((x_val, y_val))
ds_val = ds_val.map(preprocess).batch(batchsz, drop_remainder=True)
# 构建多层网络
network = Sequential([layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(32, activation='relu'),
layers.Dense(10)])
network.build(input_shape=(None, 28 * 28))
network.summary()
# 优化器
optimizer = optimizers.Adam(lr=0.01)
# build summary
current_time = datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
log_dir = 'logs/' + current_time
summary_writer = tf.summary.create_file_writer(log_dir)
# 一张图片-fed single image
# get x from (x,y)
sample_img = next(iter(db))[0]
# get first image instance
sample_img = sample_img[0]
sample_img = tf.reshape(sample_img, [1, 28, 28, 1])
with summary_writer.as_default():
tf.summary.image("Training sample:", sample_img, step=0)
for step, (x, y) in enumerate(db):
with tf.GradientTape() as tape:
# [b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28 * 28))
# [b, 784] => [b, 10]
out = network(x)
# [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# [b]
loss = tf.reduce_mean(tf.losses.categorical_crossentropy(y_onehot, out, from_logits=True))
grads = tape.gradient(loss, network.trainable_variables)
optimizer.apply_gradients(zip(grads, network.trainable_variables))
if step % 100 == 0:
print(step, 'loss:', float(loss))
with summary_writer.as_default():
tf.summary.scalar('train-loss', float(loss), step=step)
# evaluate
if step % 500 == 0:
total, total_correct = 0., 0
# 测试
for _, (x, y) in enumerate(ds_val):
# [b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28 * 28))
# [b, 784] => [b, 10]
out = network(x)
# [b, 10] => [b]
pred = tf.argmax(out, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# bool type
correct = tf.equal(pred, y)
# bool tensor => int tensor => numpy
total_correct += tf.reduce_sum(tf.cast(correct, dtype=tf.int32)).numpy()
total += x.shape[0]
print(step, 'Evaluate Acc:', total_correct / total)
# fed multi-image
# print(x.shape)
val_images = x[:25]
val_images = tf.reshape(val_images, [-1, 28, 28, 1])
with summary_writer.as_default():
tf.summary.scalar('test-acc', float(total_correct / total), step=step)
tf.summary.image("val-onebyone-images:", val_images, max_outputs=25, step=step)
val_images = tf.reshape(val_images, [-1, 28, 28])
figure = image_grid(val_images)
tf.summary.image('val-images:', plot_to_image(figure), step=step)
datasets: (60000, 28, 28) (60000,) 0 255
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 200960
_________________________________________________________________
dense_1 (Dense) multiple 32896
_________________________________________________________________
dense_2 (Dense) multiple 8256
_________________________________________________________________
dense_3 (Dense) multiple 2080
_________________________________________________________________
dense_4 (Dense) multiple 330
=================================================================
Total params: 244,522
Trainable params: 244,522
Non-trainable params: 0
_________________________________________________________________
0 loss: 2.3105626106262207
0 Evaluate Acc: 0.12740384615384615
100 loss: 0.2310105711221695
200 loss: 0.12018449604511261
300 loss: 0.1581496298313141
400 loss: 0.1331040859222412
500 loss: 0.24385929107666016
500 Evaluate Acc: 0.9512219551282052
600 loss: 0.1032937541604042
700 loss: 0.07968265563249588
800 loss: 0.244653582572937
900 loss: 0.0942125916481018
1000 loss: 0.13311226665973663
1000 Evaluate Acc: 0.9650440705128205
1100 loss: 0.06725892424583435
1200 loss: 0.09722905606031418
1300 loss: 0.07106369733810425
1400 loss: 0.13069169223308563
1500 loss: 0.18012166023254395
1500 Evaluate Acc: 0.9677483974358975
1600 loss: 0.04220552742481232
1700 loss: 0.1482035368680954
1800 loss: 0.09046145528554916
1900 loss: 0.10859175771474838
2000 loss: 0.11406847089529037
2000 Evaluate Acc: 0.9692508012820513
2100 loss: 0.07065580040216446
2200 loss: 0.0800597295165062
2300 loss: 0.06859733164310455
2400 loss: 0.092743419110775
2500 loss: 0.0571281835436821
2500 Evaluate Acc: 0.9684495192307693
2600 loss: 0.06882628798484802
2700 loss: 0.017966950312256813
2800 loss: 0.12662722170352936
2900 loss: 0.15501287579536438
3000 loss: 0.08466196805238724
3000 Evaluate Acc: 0.9698517628205128
3100 loss: 0.06166066229343414
3200 loss: 0.13097698986530304
3300 loss: 0.043429963290691376
3400 loss: 0.037568576633930206
3500 loss: 0.05409557372331619
3500 Evaluate Acc: 0.9721554487179487
3600 loss: 0.07077501714229584
3700 loss: 0.06083894520998001
3800 loss: 0.061949823051691055
3900 loss: 0.04240621626377106
4000 loss: 0.13972973823547363
4000 Evaluate Acc: 0.9725560897435898
4100 loss: 0.0429576113820076
4200 loss: 0.07576552033424377
4300 loss: 0.09691401571035385
4400 loss: 0.03496313467621803
4500 loss: 0.07032518088817596
4500 Evaluate Acc: 0.9716546474358975
4600 loss: 0.07891491055488586