“泰迪杯”挑战赛 - 通过 Logistic Lasso模型预测肝癌手术预后影响及因素

目 录

1. 研究目标
2. 分析方法与过程
   2.1. 总体流程
   2.2. 具体步骤
   2.3. 结果分析
3. 结论
4. 参考文献

1. 研究目标

本文目标为建立数据挖掘模型,研究肝癌手术预后影响(Y) （有或无）与食道静脉曲
张 $(X_1)$ ，门脉癌栓 $(X_2)$ ，HbsAg $(X_3)$ , Anti-HCV $(X_4)$ ，肿瘤部位 $(X_5)$ ，肿瘤大小 $(X_6)$，肿瘤生长方式 $(X_7)$ ，肿瘤包膜 $(X_8)$ ，肿瘤旁的微小子灶 $(X_9)$ ,术后腹水$(X_{10})$ (部分或全部)的关系，对病人的预后影响(Y) 预测，从而为病人规划最佳的手术和治疗方案。

2. 分析方法与过程

2.1 总体流程

步骤一：数据预处理：
题中所给数据已经过预处理。数据均为分类数据和有序数据，为了便于分析，将其转化为数值型数据。

步骤二：相关性检验：
由于模型需要，计算两两指标之间的相关性，相关性强的两个变量我们只选其中一个。

步骤三：模型建立：
建立 Logistic 二分类模型，进行拟合和预测。

步骤四；模型改进：
本问题由于样本数量过少，基于经典方法处理其预测能力往往比较差，我们利用最新稀疏正则化方法[1,2.3] ，开展此问题研究。稀疏正则化是指对解空间施以某种先验约束来使解具有稀疏性。我们基于 Logistic Lasso 方法研究上述问题，可有效克
服因为样本量过少而引起的弱预测能力。

步骤五：模型评价：
运用 ROC 曲线对分类器的分类效果做评价，并对模型的拟合效果和预测效果及可解释性进行评价。

步骤六：问题与思考。

2.2 具体步骤

步骤一：数据预处理
给定数据的因变量（预后影响）正负平衡，故无需删减。如下表 1 所示，变量X1到 X10 均为分类变量和有序变量，为了便于分析，将其转化为数值型变量，将 P分类数据用 P -1 维向量表示。如：将二分类变量用 0,1 表示，三分类变量用（0,1）（1,0），（0,0）表示，四分类变量用（0,0,1），（0,1,0），（1,0,0），（0,0,0） 表示。

在表 2 中，说明如下：
$X_1$ (V1,V2,V3)：（0,0,0）表示 no；（1,0,0）表示 light；（0,1,0）表示 mid; (0,0,1)表 示 serious.

$X_2$ (V4,V5): (0,0）表示 no; (1,0)表示 branch; (0,1)表示 trunk.

$X_3$ (V6): 0 表示 negative; 1 表示 positive.

$X_4$ (V7): 0 表示 negative; 1 表示 positive.

$X_5$ (V8,V9): (0,0）表示 leftliver; (1,0)表示 rightliver; (0,1)表示 allliver.

$X_6$ (V10,V11,V12):（0,0,0）表示 small;（1,0,0）表示 middle;（0,1,0）表示 big; (0,0,1) 表示 verybig.

$X_7$ (V13): 0 表示 dilation; 1 表示 infiltration.

$X_8$ (V14,V15): (0,0）表示 intergrate; (1,0)表示 part; (0,1)表示 no.

$X_9$ (V16): 0 表示 no; 1 表示 have.

$X_{10}$ (V17,V18): (0,0）表示 no; (1,0)表示 less; (0,1)表示 much.

Y (V19): 0 表示 N; 1 表示 Y

步骤二：相关性检验

由于 Logistic 回归要求各变量独立，所以对预处理后的数据进行两两相关性检验，当两两相关系数高时，适当的变量变换是可行的[3]，结果显示任何两个变量均无显著的线性相关性，故不需剔除变量，也不需要进行变量变换。结果部分如图 1所示。

步骤三：建立模型
在本文中,我们选择 Logistic 函数进行拟合和预测, 选择前 16 组数据作为训练集,后 4 组为预测集. Logistic 可以将实数轴上问题转化为[0,1]区间的问题，

$$h(x)=\frac{1}{1+e^{-{\eta }^{r}x}}$$

其中$\eta$ 为待估参数从而 h(x)>0.5 的预测为 1，h(x)<=0.5 的预测为 0。Logistic 回归是一种广义线性模型,在特征到结果的映射中加入一层函数映射，即先把特征线性求和，然后用函数 h(x)来预测。

下面介绍广义线性模型：
(1) 假设 $Y|X;\theta$ 来 自 参 数 为 η 的 指 数 分 布 族 （ 典 则 形 式 ），即为

$$P(y;\eta )=b(y)exp({\eta }^{T}T(y)-a(\eta ))$$

(2)给定 x ，目标要确定T(y) ,(通常为 y )，由于 y 的随机性，转化为确定h(x)，

$$h(x)=E(y|x)$$

（3） $\eta ={\theta }^{T}x$

图 1 相关性分析

本文研究的是二分类问题，故Y 服从伯努利分布.伯努利分布的概率可以表示为指数分布的典则形式（其中φ 为参数），

$$\begin{gathered} p(y;\varphi )={\varphi }^y(1-\varphi {)}^{1-y} \\ =exp(ylog\varphi +(1-y)log(1-\varphi )) \\ =exp(log(\frac{\varphi }{1-\varphi }))y+log(1-\varphi ) \end{gathered}$$

$$\eta =log(\varphi /(1-\varphi ))$$

从而得到：伯努利分布 $h(x)=E(y|x)=\varphi$,
$$\varphi =\frac{1}{1+e^{\eta }}$$

其中 $\eta ={\theta }^{T}x$。

在 R 中调用 glm2 程序包（glm2 为 R 中一程序包，用来处理广义线性模型）进行拟合和预测，选取前 16 个为训练集，后 4 个为测试集，结果为训练集上准确率为16/16=100%,测试集上准确率为 2/4=50%。

步骤四：模型改进：
之前建立的 Logistic 回归模型没有对变量进行选择，由于样本量仅仅为 20，预 理之后变量个数也达到了 18 个，样本量和变量个数接近。上段中模型存在以下几个题：

(1)过度拟合。由于样本数量过少，造成过度拟合。此时，模型在训练集上拟合率高，但在预测集上预测结果较差。因此，需要对模型施以某种限制,从而降低模型的拟合能力,并最终提高模型预测能力,而这种思想正是回到主流的正则化方法的基本思 想[1,2,3] 。

(2)模型的可解释性差。可解释性揭示的是事物本身的客观规律，是科学研究的根本目标，也是进一步提高泛化性的途径。

在医学中,经常地,简单模型往往更利于医生快捷判别病人病症,因此有必要进一步简化 相应影响因素,从而为医生提供一种简单易判别方法。

针对上述问题，我们对模型进行改进，建立 Logistic Lasso 正则化模型。

其中$l(.)$ 为损失函数, $\lambda {\sum }_{i=1}^{18}|{\beta }_i|$为罚函数。损失函数项度量学习结果在训练集上的误 差损失，而正则化项包含先验信息。正则化主要通过对解空间施以某种先验约束来达到某种正则解的目的。上述模型的损失函数即为 Logistic 函数的相反数，事实上为 y 的 极大似然函数的相反数，正则化项$l_1$。显然，本文中正则化是为了变量选择，提高模型的可解释性，进而提高机器泛化能力。上述模型中 λ 控制机器的复杂度，通常用交叉验证(Cross-Validation)方法选择。由于我们已经将数据进行预处理，故原有 10 个变量增加为 18 个，借鉴 Group lasso 的思想，我们对变量进行分组。由于新变量间自然的形成了某种分组关系，比如 $X_1,X_2,X_3$ 分别为食道静脉曲张（轻），食道静脉曲张（中），食道静脉曲张（重）。显然这三个变量应该为一组。具体分组如下：

组 1： 食道静脉曲张
组 2： 门脉癌栓
组 3： HbsAg
组 4： Anti-HCV
组 5： 肿瘤部位
组 6： 肿瘤大小
组 7： 肿瘤生长方式
组 8： 肿瘤包膜
组 9： 肿瘤旁的微小子灶
组 10：术后腹水

由于上述分组都是自然形成的，所以可以使拟合更准确。此时，同组中将以组形式一起影响模型。

在 R 中调用 grpreg 程序包（grpreg 为 Penalized Logistic Group Lasso Regression 的程序包），进行拟合和预测，选取前 16 个为训练集，后 4 个为测试集，结果显示训练集上准确率为 14/16=87.5%,测试集上准确率为 3/4=75%。对预后影响（Y）有影响的变量按重要程度排序为食道静脉曲张，Anti-HCV，肿瘤包膜，肿瘤旁的微小子灶。

步骤五：模型评价

（1）ROC 曲线
二分类问题，即将实例分成正类（Positive）或负类（Negative）。对一个二分类问题来说，会出现四种情况。如果一个实例是正类并且也被 预测成正类，即为真正类（True positive）,如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如 果实例是负类被预测成负类，称之为真负类（True negative）,正类被预测成负类则为假 负类（False negative）。列联表如下表所示，1 代表正类，0 代表负类。从列联表引入

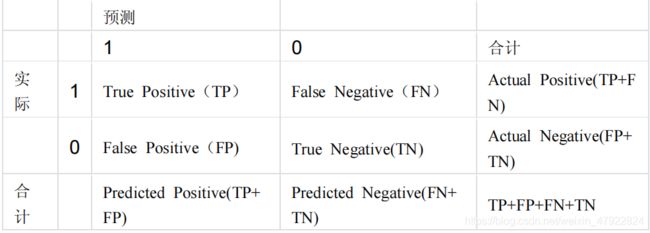
其中，每个单元格中元素表示属于相应类别的个数。注:两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为 TPR=TP/ (TP+ FN)，刻画的是分类器所识别出的 正实例占所有正实例的比例。另外一个是负正类率(false positive rate, FPR),计算公式为 FPR= FP / (FP + TN)，计算的是分类器错认为负类的正实例占所有负实例的比例。还有一个真负类率（True Negative Rate，TNR），也称为 specificity,计算公式为 TNR=TN/ (FP+ TN) = 1 - FPR。

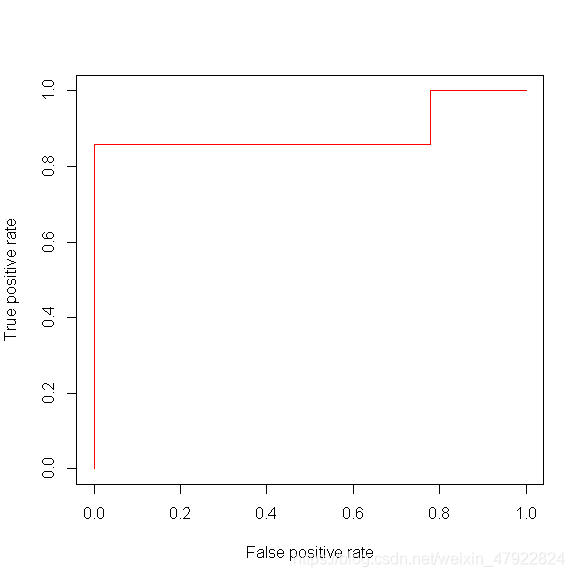
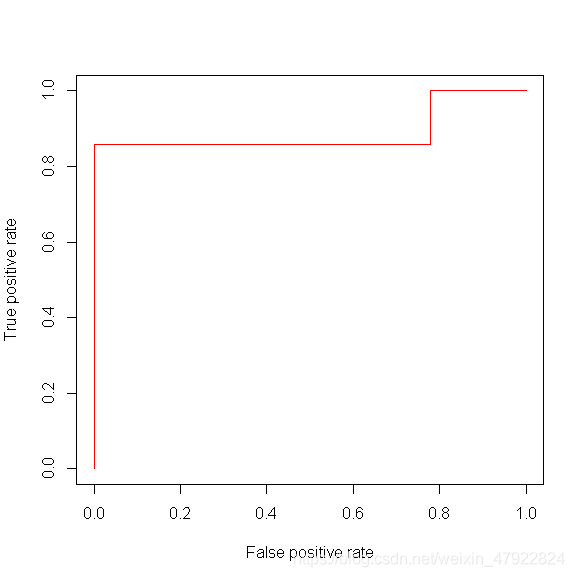
在一个二分类模型中，对于所得到的连续结果，假设已确定一个阀值，比如说 0.6，大于这个值的实例划归为正类，小于这个值则划到负类中。如果减小阀值，减到 0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例 的比类，即 TPR,但 类似于假设检验中第一类错误和第二类错误的关系，同时也将更多的负实例当作了正实 例，即提高了 FPR。为了形象化这一变化，在此引入 ROC。上述模型的结果对应的 ROC曲线如下图：

图 2 ROC 曲线图

研究表明，AUC（Aera under the curve）（ROC 曲线下方的面积）可以反应分类器性能的好坏,AUC 越大，表示分类器的性能越好。如图 2 显示，我们的分类器性能较好。

(2)改进后的模型对变量进行了选择和排序，同时拟合精度为 14/16= 87.5% ,预测精度为 3/4=75% ,较改进前的模型均有显著提高。可以看出通过加罚项，改善了模型的拟合精度，泛化性和可解释性。指标个数由之前的 10 个减少为 4 个，按重要程度排序为食道静脉曲张，Anti-HCV，肿瘤包膜，肿瘤旁的微小子灶，而且选择的变量从医学角 度来说也符合常规。当病人的各项指标已知时，我们可以根据我们的模型来对病人进行分类，预测术后是否有预后影响，从而可以对病人的手术方案进行设计和调整。

步骤六：问题与思考
（1）我们利用支持向量机（Support Vector Machine）对本问题做了研究。SVM 是一种高效分类方法，是基于最大化几何间隔的算法。结果显示，SVM 的拟合准确率为16/16=100%,预测准确率为 2/4=50%,所以 SVM 也存在过度拟合的问题。SVM 和 Logistic 回归相比拟合与预测精度均一致，但与 Logistic Lasso 相比，SVM 的预测较差，且 SVM无变量选择作用。

(2)为了提高预测精度，可以研究与问题相关的罚函数，比如借鉴SCAD[2,3], LI /2[4]的思 想，同时考虑医学方面的先验信息，建立模型，从而有效提高模型的解释和预测能力。

2.3程序与结果分析 程序与结果分析

(1)相关性分析的 R 程序如下：

library(grpreg) 
data <- read.csv("C:/Documents and Settings/Administrator/桌面/数据挖掘/新建
Microsoft Excel 工作表 (2).csv", head = FALSE) 
data1<-as.matrix(data) 
cor(data1)

结果如图 3 所示

图 3 相关性分析程序结果

(2) 使用 logistic 回归的 R 程序如下：

library(glm2) 
mydata <- read.csv("C:/Documents and Settings/xyzx/桌面/16.csv", head = FALSE) 
beta<-glm(V19~V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V13+V14+
V15+V16+V17+V18,mydata,family='binomial') 
label13<-(predict(beta,mydata)>0.5) 
sum(label13==mydata$V19) 
summary(beta) 
newdata<-read.csv("C:/Documents and Settings/xyzx/桌面/4.csv", head = FALSE) 
newdata$rankP <- predict(beta, newdata = newdata, type = "response") 
newdata

结果如图 4 所示。
结果显示：训练集上准确率为 16/16=100%,测试集上准确率为 2/4=50%。
说明模型拟合非常好，预测不太好。具体原因如前文所述。

(3)使用 Logistic Lasso 回归的 R 程序如下：

library(grpreg) 
data <- read.csv("C:/Documents and Settings/xyzx/桌面/新建 Microsoft Excel 工作表
(2).csv", head = FALSE) 
group1<-cbind(data[,1],data[,2],data[,3]) 
group2<-cbind(data[,4],data[,5]) 
group3<-cbind(data[,6]) 
group4<-cbind(data[,7]) 
group5<-cbind(data[,8],data[,9]) 
group6<-cbind(data[,10],data[,11],data[,12]) 
group7<-cbind(data[,13]) 
group8<-cbind(data[,14],data[,15]) 
group9<-cbind(data[,16]) 
group10<-cbind(data[,17],data[,18]) 
testset<-c(17,18,19,20) 
x_sub<- cbind(group1,group2,group3,group4,group5,group6,group7,group8,group9,group10) 
x_sub1 <- x_sub[-testset, ] 
x_pre <- x_sub[testset, ] 
y_sub<- as.numeric(data[,19]) 
y_sub[which(y_sub>0)]<-1 
y_sub1 <- y_sub[-testset] 
y_pre <- y_sub[testset] 
group<-c(1,1,1,2,2,3,4,5,5,6,6,6,7,8,8,9,10,10) 
fit1<- grpreg(x_sub1,y_sub1,group,penalty="grLasso",family="binomial") 
lambda<- select(fit1,"AIC")$lambda # choose the regularization parameter 
beta<- select(fit1,"AIC")$beta # output fitted coeficients 
beta 
y_fit<- predict(fit1, x_sub1, type="class", lambda) 
sum(y_fit==y_sub1) 
y_fit_pre <- predict(fit1, x_pre, type="class", lambda) 
sum(y_fit_pre==y_pre)

执行结果如下图 5 所示：

图 5 Logistic Lasso 回归程序结果

结果显示：训练集上准确率为 14/16=87.5%,测试集上准确率为3/4=75%。对预影响(Y)有影响的变量按重要程度排序为食道静脉曲张，Anti-HCV，肿瘤包膜，肿瘤旁的微小子灶。

可以看出，改进之后的模型对变量进行了选择和排序，选出了对Y 影响较大的四个指标，且这四个指标也符合医学经验，从而提高的模型的可解释性。此外，虽然拟合精 度较改进前的模型下降，但预测精度显著提高。正好说明了样本误差与逼近误差的关系， 即样本误差增大导致逼近误差减小。

（4）支撑向量机（SVM）的 R 程序如下：

library(e1071) 
library(rpart) 
mydata <- read.csv("C:/Documents and Settings/xyzx/桌面/新建 Microsoft Excel 工作表
(2).csv", head = FALSE) 
index <- 1:20 
testindex <- c(17,18,19,20) 
testset <- mydata[testindex,] 
trainset <- mydata[-testindex,] 
svm.model <- svm(V19~ ., data = trainset, cost = 100, gamma = 1) 
svm.pred <- predict(svm.model, testset[,-19]) 
label13<-(predict(svm.model,trainset[,-19])>0.5) 
sum(label13==mydata[-testindex,19]) 
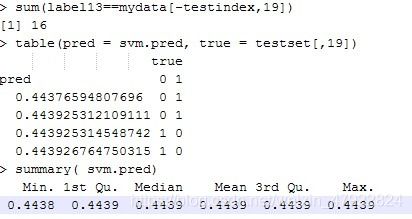
table(pred = svm.pred, true = testset[,19]) 
summary( svm.pred) 
summary( svm.model )
print(svm.pred)

结果如下图 6 所示：

图 6 SVM 程序结果

结果显示：训练集上准确率为 16/16=100%,测试集上准确率为 2/4=50%。

(5)ROC 曲线的 R 程序如下：

library(ROCR) 
y_fit3<- predict(fit1, x_sub1, type="response", lambda) 
pred <- prediction(y_fit3, y_sub1) 
perf <- performance(pred, measure = "tpr", x.measure = "fpr") 
plot(perf, col=rainbow(10))

结果如下图 7 所示：

图 7 ROC 曲线

AUC 图显示，本文提出方法是高效的。

3. 结论

对肝癌病影响的主要因素问题,临床表明,影响肝癌预后影响的因素为 食道静脉曲张、门脉癌栓、HbsAg、 Anti-HCV 、肿瘤部位、肿瘤大小、肿瘤生长方式、肿瘤包膜、肿瘤旁的微小子灶、术后腹水 10 个。本文研究上述因素在肝癌病影响中的重要性，并通过建立新的模型，研究肝癌病人的预测问题。

对于上述问题，我们先检验肝癌手术预后影响的主要因素之间的线性相关性，通过相关性强弱对某些指标进行适当的删减。然后基于 Logistic 回归 对预处理后的数据进行拟合和预测，进一步，我们基于最新的稀疏正则化方法改进模型。我们基于 Logistic Lasso回归模型再次研究肝癌手术预后影响的主要因素及预测。通过对系数施以稀疏约束，研究了肝癌手术预后影响的主要因素并排序。

选择前 16 组数据作为训练集，后 4 组数据作为测试集，新模型在训练集上拟合准确率为 14/16=87.5%,在测试集上准确率为 3/4=75%。结果显示：食道静脉曲张，Anti-HCV，肿瘤包膜，肿瘤旁的微小子灶为主要因素。同时 ROC 曲线说明我们的分类器性能良好，且上述结果符合医学先验。

针对肝癌手术预后影响因素问题,我们做了相关性检验，Logistic Lasso 回归,以及用 ROC 曲线进行检验。最终结果显示分类效果较好，但不足之处是未能与医学先验信 息结合。因此进一步开展结合先验信息的新模型新方法研究是一项有意义的工作。

4. 参考文献

[1] Robert Tibshirani. Regression Shrinkage and Selection via the Lasso. Robert Tibshirani Journal of the Royal Statistical Society. Series B (Methodological), Vol. 58, No. 1,2011,05,01

[2] 张海,王尧,常象宇,徐宗本. L1/2正则化.中国科学 信息科学,2010,40:412-422

[3]Jianqing Fan and Jinchi Lv . A Selective overview of Variable Selection in High Dimensional Feature Space.2009,arXiv:0910.1122.

[4]Van de Geer,S…High-dimensional generalized linear models and the LASSO.Ann. Statist.2008,36,614-645 .