“泰迪杯”挑战赛 - 基于协同过滤的设备维修信息数据挖掘(详细数据及代码)

目录

1. 挖掘目标
2. 分析方法与过程
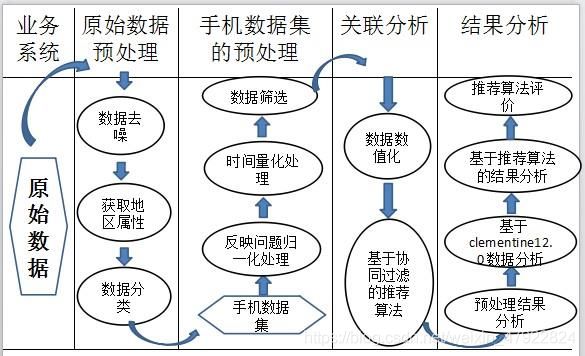
   2.1. 总体流程
   2.2. 具体步骤
   2.2.1. 维修数据集的特点分析 2.2.2. 维修数据集的预处理
   2.2.3. 关联分析
   2.3. 结果分析
   2.3.1 预处理的结果分析
   2.3.2 手机数据集基于 Clementine 结果分析
   2.3.3 基于推荐算法的手机数据集分析
   2.3.4 推荐算法的评价
3. 结论
4. 参考文献
5. 附件

1. 挖掘目标

本次建模目标是利用维修记录的海量真实数据，采用数据挖掘技术，分析手机各类故障与手机型号、手机各类故障与市场的相互关系，构建反映各类型号手机的常见故障评价指标体系、不同市场和地区手机质量的评价体系，为手机公司的设备储藏提供意见，同时也可为消费者提供购买意见。

2. 分析方法与过程

2.1. 总体流程

本文主要包括如下步骤：

步骤一：维修数据集的特点分析

分析原始维修数据集的特点，发现客户要求服务类型中安装记录与维修记录条数持平；数据缺失严重部分主要集中在购买商场、购机价格、机型属性、工程单号、工程总数、多次维修内机编号、故障原因代码、故障原因描述、维修措施这几个属性；数据噪声严重的部分集中在购机价格、产品型号。

步骤二：数据的预处理及筛选

首先对数据进行去噪处理，并且根据原始数据的“服务商代码”属性进行“服务商所在地”属性的提取。接着对数据集中的各项数据进行统计分析，为了方便进行更深入的研究，选取手机数据集进行进一步的数据挖掘研究。同样需要对手机数据集进行进一步的数据预处理，将“反映问题描述”属性的属性值进行归一化处理，根据购机日期属性及预约日期属性提取手机使用时长。并且利用 clementine12.0 软件分析得知“反映问题描述”属性与手机使用时长、市场级别、服务商所在地区、产品型号相关性较强。

步骤三：利用基于协同过滤的个性推荐算法进行关联分析

基于预处理后的高质量的手机数据集，采用基于协同过滤的个性推荐算法对手机数据集中的属性进行关联分析，并对该设备生产企业的备件储备需求进行预测分析、潜在故障预警分析、易损件及原因分析等方面进行探索分析。

2.2. 具体步骤

2.2.1. 维修数据集的特点分析

设备生产企业伴随着销量的增加，维修也在不断增加，随着时间的推移，越来越多的维修记录被存储到数据库中。当这些数据量积累到一定程度时，必然反映出一定的规则。但是在记录维修数据时，由于人工操作的失误以及客户的遗忘，使得了维修数据集存在缺失、噪声，而这些数据又影响着最终的结果。为了得出比较精确的决策，需先对数据集进行分析处理。从数据库中导出某设备生产企业的 685413 条维修记录数据，从该维修数据集分析可以得出以下特点：

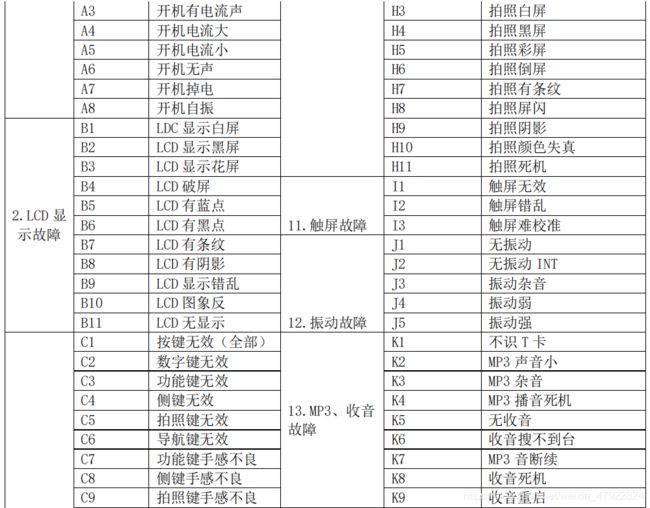
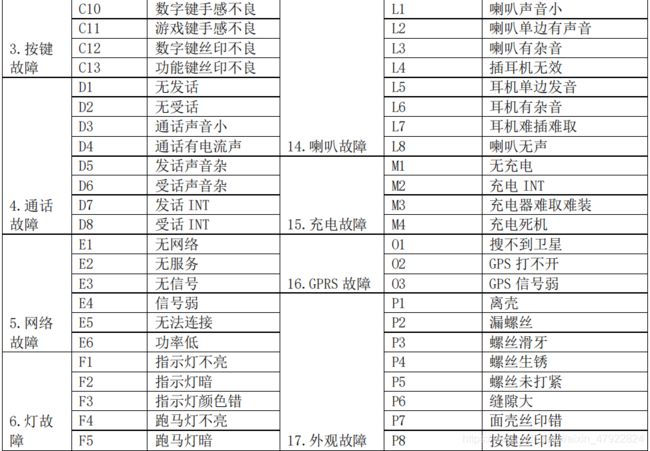
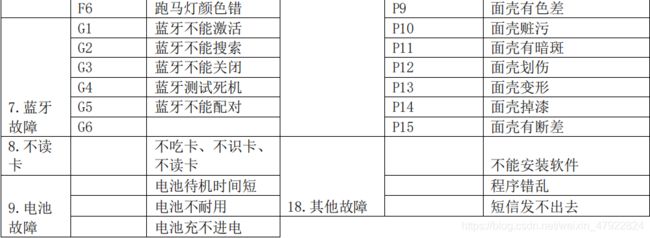
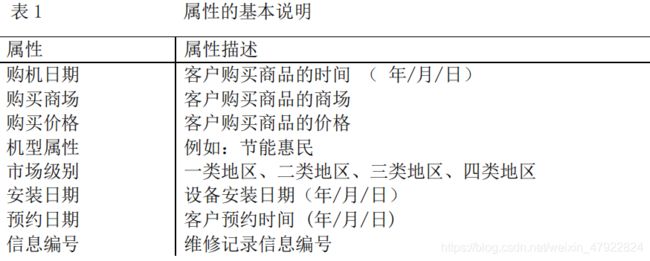
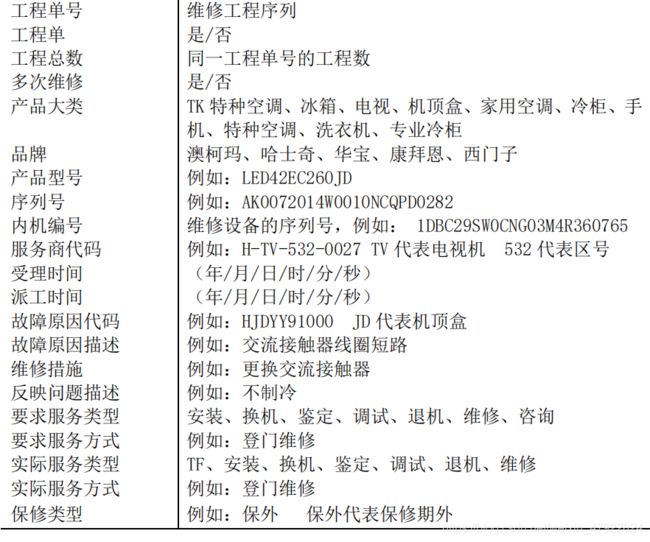
(1) 每条维修记录提供了 29 个属性，属性的基本说明如表 1 所示：

(2) 对数据集中的要求服务类型进行统计，客户要求服务类型为维修的数据记录有314132 条，而安装的数据记录有 302824 条，与维修记录条数持平。因此可以得出该维修数据集不仅仅是商品需要维修的维修记录，而是商品售后服务的记录。

(3) 对数据集中的预约时间进行分析，可以发现预约时间全部在 2013-9 内，因此我们所获得的数据集是该设备生产企业 9 月份中客户预约维修的维修记录，即设备生产企业一个月内的维修工作。

(4) 数据集中各项属性存在部分或大量的数据缺失，缺失严重部分主要集中在购买商场、购机价格、机型属性、工程单号、工程总数、多次维修内机编号、故障原因代码、故障原因描述、维修措施这几个属性。

(5) 数据集中存在噪声数据，噪声严重的部分集中在购机价格、产品型号。由于客户忘记了当初的购机价格、填写价格错误等原因，该数据集中有 484164 条数据记录显示购机价格为 0。同样，可以认为由于工作人员登记方式不同，使得产品型号中存在大量噪声数据—型号的末端存在异常，例如“BCD-398WT-J，”。

2.2.2. 维修数据集的预处理

（1）缺失数据的处理
由于数据集中的数据量大，同时数据中的缺失部分规律不明显，无法找到合理的补充数据规律，那么在数据缺失严重的属性中随意或有限度的补充数据不仅会影响数据的筛选甚至会影响最终的结论。因此在该步骤中不对缺失数据进行处理，而是在后面的处理中针对不同问题对缺失数据进行处理。

（2）噪声数据的处理
利用 excel 表格对数据集中产品型号的错误数据进行修正，去除末端存在异常的型号的末端：选择产品型号——数据——分列——分隔符号——逗号。由于型号与价格的关联不明显，而且有 484164 条价格记录是由于客户忘记当初的购机价格而填写为 0，从剩余的价格记录中难于寻找合理的规律修正错误的价格，因此不对错误价格进行修正。

（3）服务商所在地区的提取
数据集中并没有直接提供服务商的所在地，即提供产品售后服务机构的所在地，但是可以从服务商代码中提取出服务商所在地。利用 excel 表格提取服务商所在地，由于区号在服务商代码的第二个‘-’和第三个’-’之间，因此对于服务商所在地的提取公式为：

MID(服务商代码,FIND("-",服务商代码,3)+1,3)

例 如 ： excel 表格中 R58 的 服 务 商 代 码 “ H-SJ-010-0014 ”， 提 取 公 式MID(R58,FIND("-",R58,3)+1,3)可得到 010。010 代表服务商所在地的区号，通过网上查找可得 010 是北京的区号，即可得出该服务商所在地为北京。

（4）数据的筛选
从数据的分析中可知道数据集中含有的 7 种服务要求类型以及 10 种产品大类，从数据集中筛选出安装数据记录，其余的可归为维修记录。利用excel表格做分析如下：

图 1 维修和安装记录分布

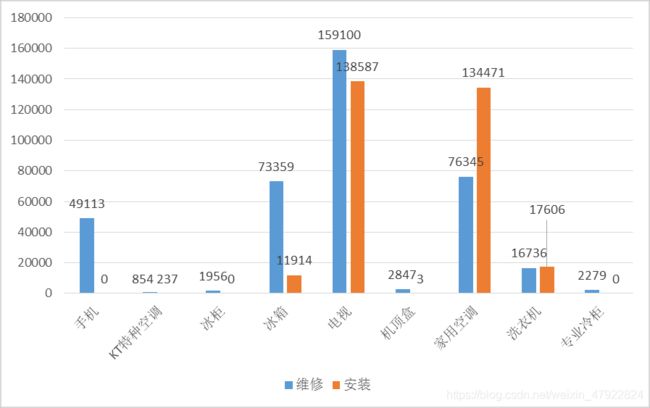
由于不同产品其隐含的规则不同，不能全部一起讨论，需先逐一分析各个产品，而分析方法都相同，不需要对全部进行讨论，只需提取其中的一种产品进行详细的分析，其他产品的分析过程类似。通过观察图 1，得知手机只有维修记录，并且记录数不少，便于分析挖掘其中隐含的规则且不失一般性，因此下面将选择手机进行深入挖掘研究。

（5）手机数据集的预处理

在数据挖掘整体过程中,海量的原始数据中存在着大量杂乱的、重复的、不完整的数据，严重影响到数据挖掘算法的执行效率，甚至可能导致挖掘结果的偏差。为此，在数据挖掘算法执行之前，必须对手机数据集进行预处理，以改进数据的质量，提高数据挖掘过程的效率、精度和性能。

1） 反映问题描述属性的归一化处理
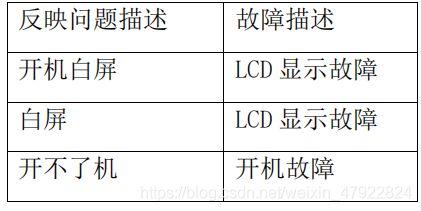
由于数据集中反映问题的描述没有一定的标准，因此对于相同的手机故障，客户反映问题的描述也是各样，例如针对手机白屏问题，就有“开机白屏”和“白屏”这两种不一样的表示方式。不一样的标准不仅影响其他属性与反映问题描述属性进行关联规则分析，更严重影响了研究手机某型号设备出现的常见故障现象，因此需要对反映问题描述属性进行归一化处理。

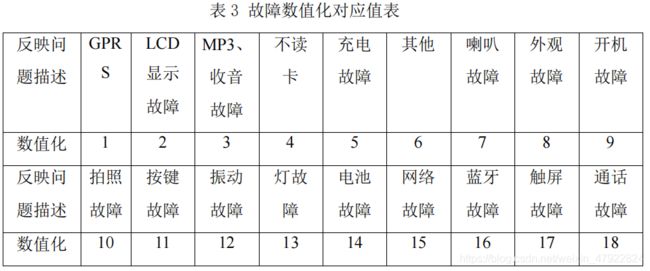
根据手机故障原因标准准则（见附录 1），利用 excel 表格通过筛选包含相同字样的数据记录，并进行替换。例如：

2）客户手机使用时长的量化处理
根据多次维修属性的反映，每条记录均为否或空白，因此可以假设客户的手机均为第一次维修。观察数据发现购机日期有 430 个缺失数据，而最早的购机日期为 2011-10-10，故使用 2011-10-01 填补空缺数据。将预约日期减去购机日期所得即为客户手机使用时长。

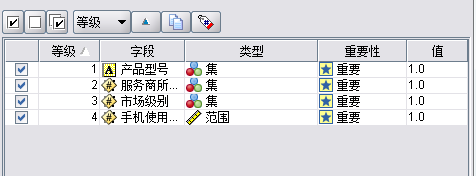
3）手机数据集属性的筛选
由于本文的研究目的在于研究手机常见故障与手机型号、手机各类故障与市场的相互关系，而原始数据共有 29 个属性，所以为了提高算法的的效率和精度，本文只需要对购机日期、预约日期、市场级别、服务商代码、产品型号、反映问题描述进行分析即可。由于服务商代码、产品型号、反映问题描述存在缺失数据，而缺失部分规律不明显，无法找到合理的补充数据规律，所以在此采用忽略缺失数据的处理方法。

将归一化处理后的“反映问题描述”属性与手机使用时长(上述购机日期与预约日期的关联后得到的数据)、市场级别、服务商所在地区(从服务商代码中提取出来的)、产品型号 4 个属性进行变量重要性分析。使用 clementine12.0 软件，通过 Modeling 卡中的 Feature Selection 节点对上面的属性进行变量重要性的分析后得知“反映问题描述（以下简称故障）”属性与手机使用时长、市场级别、服务商所在地区（以下简称地区）、产品型号相关性较强。（见图 2）

图 2 变量重要性分析

2.2.3. 关联分析

随着数据库中的数据量急剧增长，人们获取自己感兴趣的信息越来越困难，面对海量的数据，每个用户希望获取的信息可能仅仅是其中很少的一部分，同时用户的需求常常是模糊的、不明确的，可能会对某些信息存在着潜在的喜好。如果服务提供者能够把信息推荐给用户，就可能把用户的潜在需求变为现实进而盈利。在这种背景下，推荐系统应运而生，推荐系统的实现方法众多，其中基于协同过滤推荐算法理论上可以推荐世界上的任何一种东西，适用性强，也是一种最成功的推荐系统算法。

文本上述研究表明手机使用时长、市场级别、地区、产品型号与故障属性都具有关联，但是各属性的对象很多，而且手机维修记录数目也达到了 47000 多条，这导致了设备生产企业难于分析备件的常见故障及潜在故障预测。查找文献了解到 Apriori 算法基于关联规则的推荐算法的基本算法，利用 clementine12.0 软件进行基于 Apriori 算法的关联规则分析，但是发现结果的支持度及置信度较低。

基于协同过滤的个性推荐算法可以很好的解决该类问题。通过推荐算法可以分析反映问题描述属性与其他属性的关联规则，产生推荐项目，从而构建反映各类型号手机的常见故障评价指标体系、不同市场和地区手机质量的评价体系，为手机公司的设备储藏提供意见，同时也可为消费者提供购买意见。因此本文选择基于协同过滤的个性推荐算法建立模型，进行属性间的关联分析挖掘，完成推荐。

（1） 数据数值化
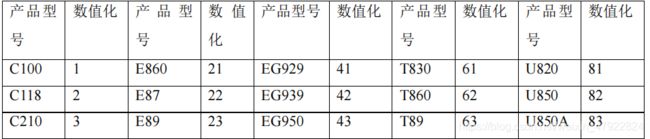
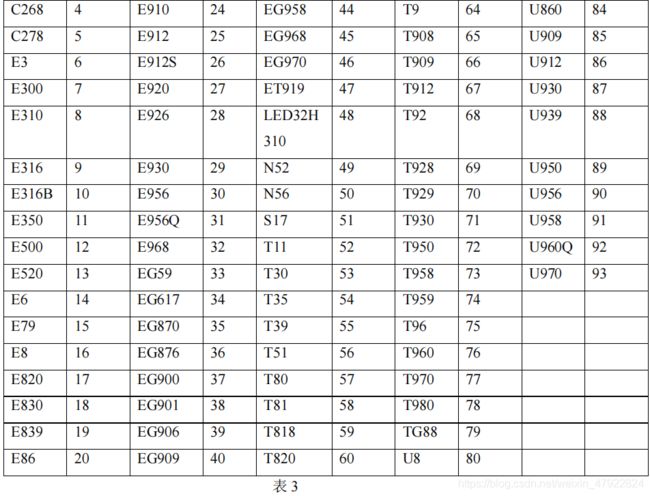
通过上述的数据处理步骤后得到的手机数据集，包括以下五个属性：使用时长（数值型）、市场级别(字符型)、产品型号（字符型）、地区（字符型）、故障（字符型）。为了方便进行基于协同过滤的个性推荐算法的数据挖掘，需要将属性的数据均数值化。可利用 excel 表格手动将上述属性进行数值化处理，如市场级别属性的处理，其他属性均可如此处理，但是产品型号的类别较多，手动处理耗时，可利用 Matlab 编写函数文件对其数值化。（程序代码见附录 2，属性所对应的数值化可见附录 3 及附录 4）

（2） 基于协同过滤的个性推荐算法的描述

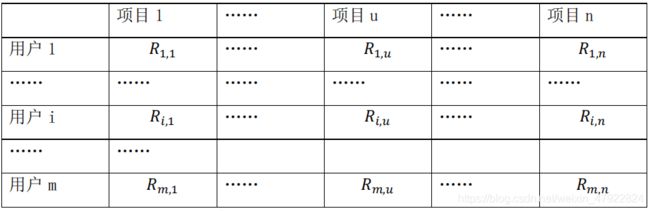
1） 伪用户_项目评分矩阵的构建———用户偏好描述
收集有关用户偏好信息，如用户对商品的评分，通过对原始数据进行清理、转换和录入，最终形成一个 m×n 维矩阵。其中行代表用户，列代表项目。如下表 2 所示，$R_{i,u}$表示第 i 个用户对项目 u 的评分值,评分值为数值型。

2） 相邻用户矩阵的构建-----寻找最近邻居

在评分矩阵中，用户已评分的项目为实际的评分值，未评分项目用 0 表示。如果用户评分被看作是 n 维项目空间上的向量，余弦相似性就是将用户的相似性通过向量间的余弦夹角度量。设用户 i 和用户 j 在 n 维项目空间上的评分分别用$R_i$,$R_j$表示,在用户 i 和用户 j 之间的相似性计算公式如下所示：

$$sim(i,j)=cos(i,j)=\frac{R_i\cdot R_j}{||R_i||\times ||R_j||}$$

①

3） 产生推荐
最近邻居集产生后，可计算目标用户对项目的预测评分值进行 Top-N 推荐。通过预测评分值搜索最近邻居而产生推荐，预测评分计算公式如下：
$$P_{i,y}=\overline{R_i}+\frac{{\sum }_{j\in NN,y\in N}sim(i,j))(R_{j,y}-\overline{R_J})}{{\sum }_{j\in NN,y\in N}sim(i,j)}$$

②

其中，$P_{i,y}$代表目标用户 i 对项目 y 的预测评分值；$\overline{R_i}$为用户 i 的平均评分值；$R_{j,y}$表示目标用户 i 的最近邻居集的用户 j 对项目 y 的评分。在此，目标用户 i 的最近邻居集用 NN 表示。按评分预测值$P_{i,y}$的高低排序产生推荐集。

（3） 建立各地区常见故障的预测推荐

协同过滤算法需要整理用户的评分数据、计算相似性、寻找最近邻居从而完成推荐。但是对于本文以手机数据集为记录集，研究地区属性与反映问题描述属性之间的关联获得各地区中最常见故障集而言，各地区对反映问题描述并没有显式的评分，这需要 Web挖掘算法来获得隐式的评分数据。基于 Matlab，构建算法的步骤如下：

1）地区_故障评分矩阵的构建

地区与故障的关联可通过手机数据集中的记录条数反映。由于原始的手机数据记录集已表明该客户并没有多次手机维修记录，因此地区 i 对故障 y 的评分可用在地区 i 的故障集中故障 y 的记录条数表示。但是考虑到手机使用时长并不完全相同，其分布如图6 所示。客户当月购买的手机当月便进行维修，可见该手机的发生故障的概率是很大的，因此对该条记录，维修次数可修正为手机数据集中最大的使用时长减去当前记录的使用时长。假设$R_{i,u}$代表地区 i 对故障 u 的评分值， $T_w$代表使用时长，那么$R_{i,u}=Ma{x}_{w\in N}(T_w)-T_d(d\in i,u)$。根据该方法计算各地区对所有故障的评分值，形成地区的评分矩阵。

2）寻找最近邻居并进行推荐
寻找地区的最近邻的关键是计算各地区之间的相似性。可利用余弦相似性的计算方法，即公式①，通过地区与故障之间的评分矩阵计算相似度得到各地区之间的相似值所组成的矩阵 sim(m，m)，并通过 acos()函数得到数值均处于 0 和 1 之间的矩阵。对于地区 i 而言，把计算出的所有相似值按照从小到大选出若干个相似值小于α的作为其最近邻居集。

得到各地区的最近邻居集后，利用公式②，可得到各地区对于所有故障的预测评分矩阵$P_{mn}$，按照评分预测值$P_{i,y}$的高低对地区 i 产生故障推荐集，该集代表地区 i 常出现的故障。(程序代码见附录 7)

该模型具有较大的灵活性。不仅可以进行各地区的潜在故障预警分析，从而实现企业在各地区的备件储备需求预测，还可以按支持度大小反映各手机型号设备出现的常见故障，只需要将手机型号作为用户、故障作为项目，直接运行程序即可。同时，由于手机维修属于送修类型，客户购机的地区并一定就是服务商所在地 ，从而手机数据集中的市场级别属性与服务商所在地属性的关联不显著。因此，可利用该模型对市场级别属性与产品型号属性进行关联分析，预测各市场级别最常出现故障的手机型号。

2.3. 结果分析

2.3.1 预处理的结果分析

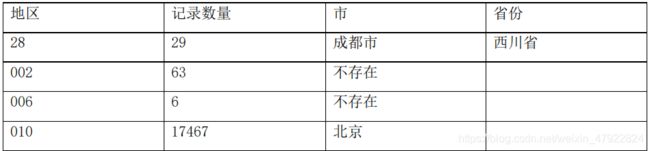
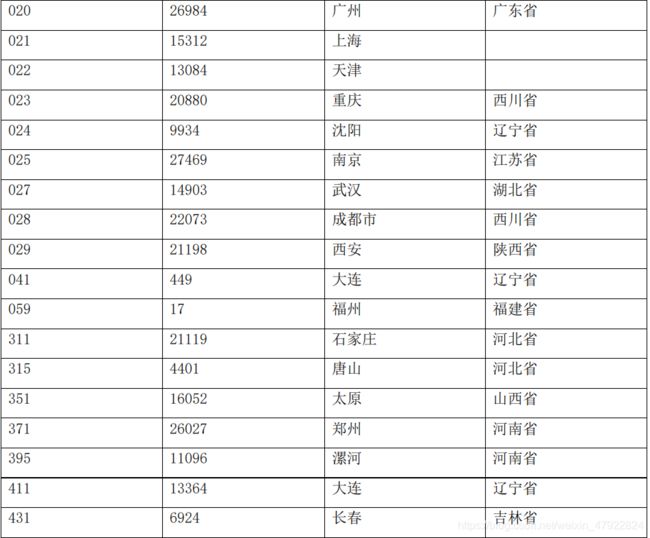
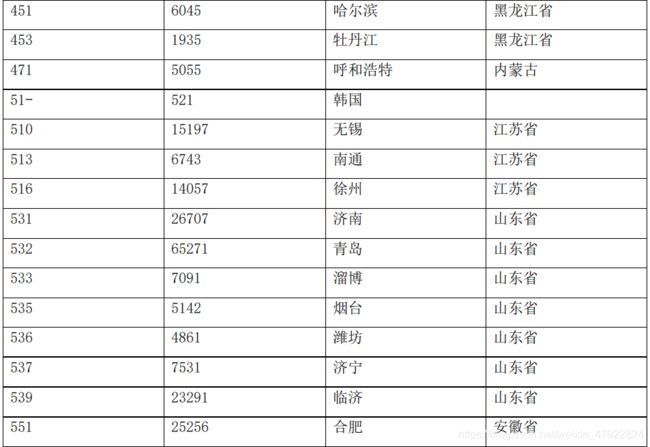
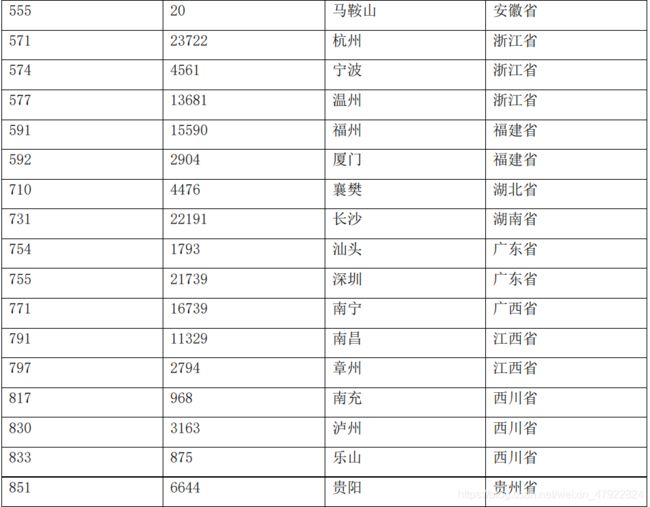
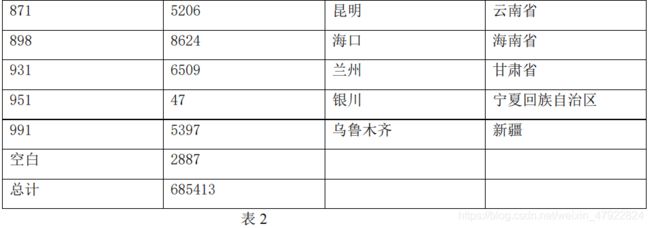
根据服务商代码属性提取出地区属性，并根据各地区归纳到各省份（见附录 3 表 2）。

图 3 各地区的手机记录分布图

图 4 品牌分布情况

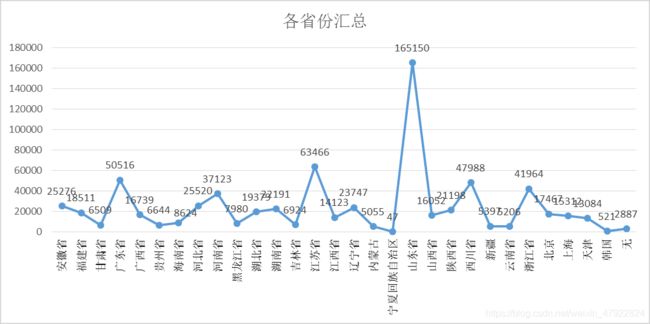
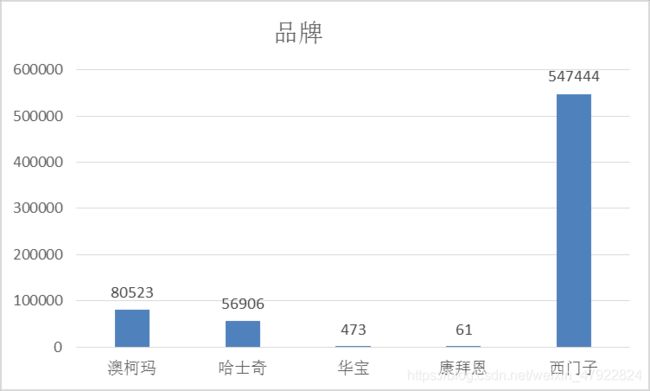
结论：从图 3 中可以发现维修记录基本囊括了全国各省，除西藏、清海省，表明了该设备生产企业是一个全国性的企业。同时山东省的维修记录数目远远大于其他各省份，可以认为山东省是该设备生产企业的总部所在地.从图 4 可以发现西门子的比重远远大于其他品牌，同样可以认为西门子是该企业的自身品牌。通过网上搜索查找，可以发现西门子本非山东省的本土品牌。因此可以认为该数据集中的品牌是经过某种规则映射而成的。

2.3.2 手机数据集基于 Clementine 结果分析

(1)基于 Apriori 的型号与故障关联分析

图 5 基于 Apriori 的型号与故障关联

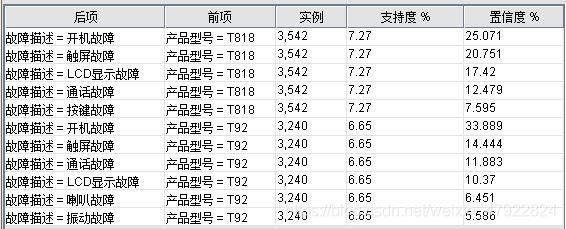
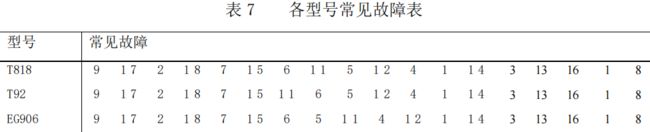
按手机型号的支持大小，可以发现型号 T818 的支持度最高，但是仅仅达到 7.27%，而其最常见的故障分别为开机故障、触屏故障、LCD 显示故障、通话故障、按键故障。对于支持度为 6.65%的 T92 而言，最常见故障如图 5 所示。

(2)使用时长属性分析

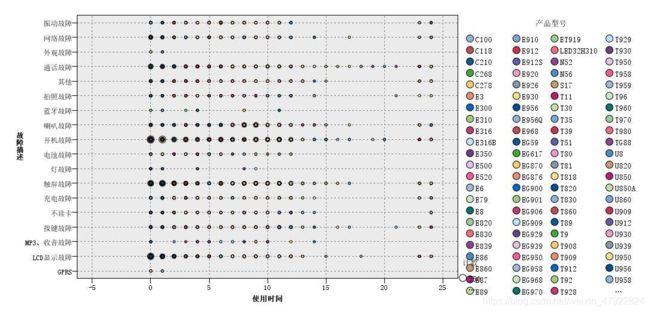
1. 使用时长，产品型号与故障的散点图

图 6

结论分析：图 6 中散点的大小表示数量的多少，可看出不同种手机型号的手机故障都主要集中在开机故障，LCD 显示故障，触屏故障和通话故障；在短时间内进行手机维修的比较多，而使用时间较长的维修数比较少。因为现在手机更新快，价格合理，同时跟据人类消费心理，当顾客购买的手机在短时间内出现故障问题，基本会选择维修，但是如果手机使用时间长并且出现了故障，顾客就会选择直接换手机，而不是维修。因此在手机的维修数据集中手机已使用时长较短时长的比重大，使用时间长的数据偏少。

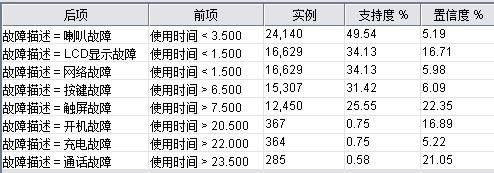
2. 手机使用时长与故障的 GRI 关联分析

图 7

结论分析：虽然支持度或置信度不是很高，但也能够大概反映一些信息：最近买的手机(使用时长在两个月内)主要的故障集中在 LCD 显示故障和网络故障；使用时间比较长的手机主要故障集中在通话故障，充电故障和开机故障。

2.3.3 基于推荐算法的手机数据集分析

(1) 各地区常见故障的预测结果分析
1）地区_故障的评分值矩阵$R_{mn}$
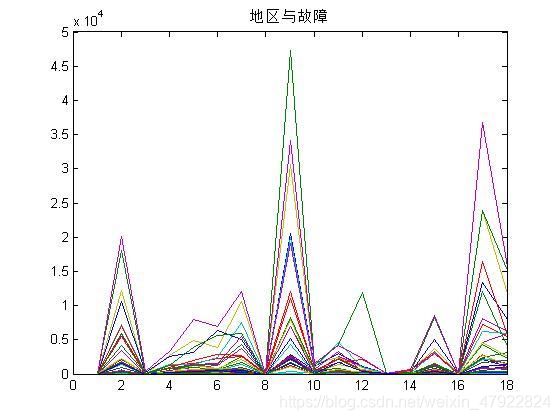
根据，利用 Matlab 软件，运行程序（见附录 6）生成地区与故障的评分图如下所示。其中 x 轴代表数值化的故障，y 轴代表地区 i 对故障 u 的评分，不同颜色的线段代表各地区。从图中可以看出各地区在 x=2,9,15,17，即 LCD 显示故障、开机故障、网络故障、触屏故障，比较集中，并且各地区对所有故障的数量趋势一样。其中山东省的地区 531 的开机故障尤其突出。

图 8

2）地区的最近邻 sim(m,m)

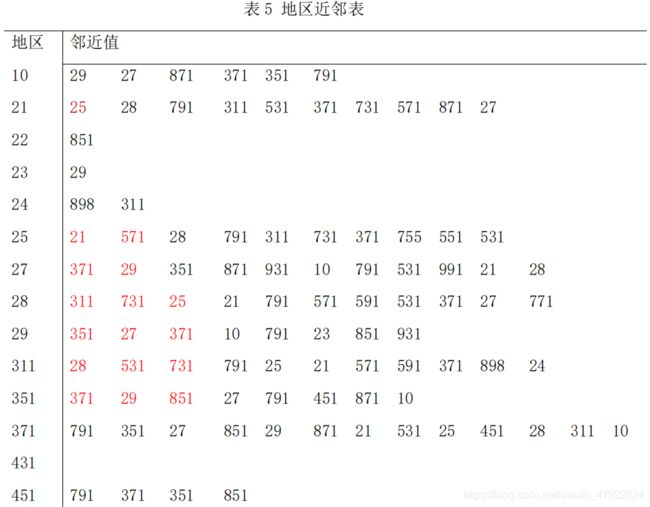
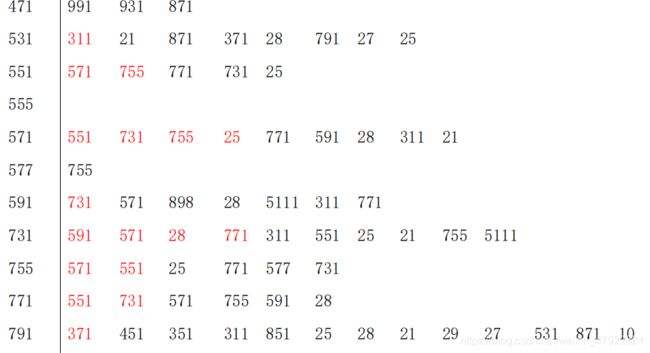
当取α=0.3，各地区产生的最近邻如下表格所示，当取α=0.2 时，各地区产生的最近邻如下表格的红色字体部分所示。由表格可以发现，当α=0.2 时，通过查看地（见附录 5）可以发现各地区的最近邻从地理位置上而言也是其近邻，这表明了地理位置上相近的地区具有相似性。因此地理位置上相近的地区，其常见手机常见故障也类似。

3）各地区常见故障预测

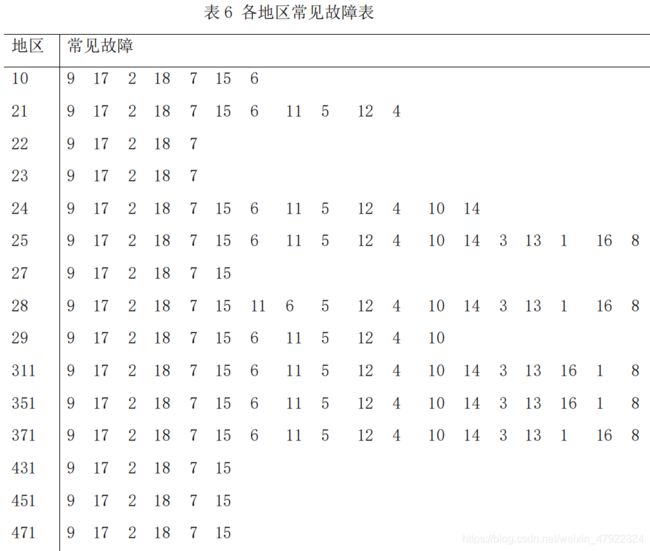
运行程序（附录 7）观察结果，可得到如下结论：每个地区的手机故障主要是：开机故障，触屏故障，LCD 显示故障和通话故障。同时这四类手机故障在手机数据集中所占的比重是很大的，而根据推荐结果分析，可以发现各地区的常见手机故障都是这几类故障，表明了该品牌的手机出现故障与各地区的关联较低。

4)不同手机型号的常见故障预测

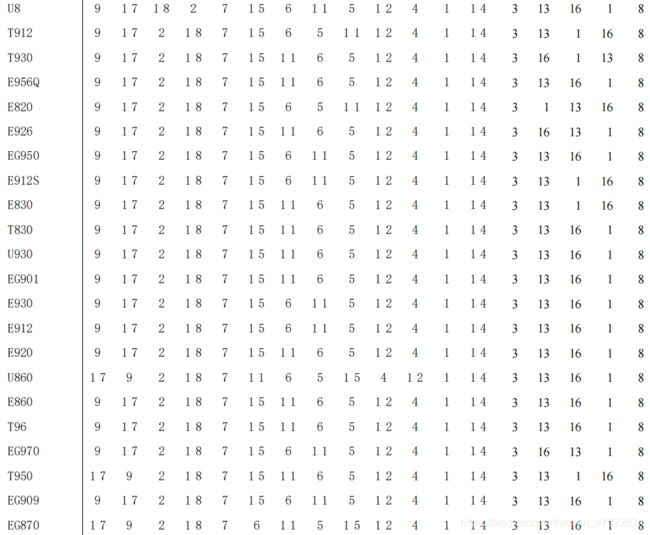
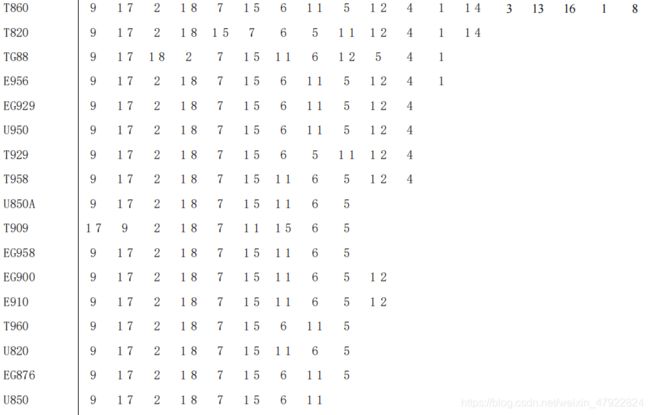
结论分析：按维修记录支持度大小对型号进行排序，其中支持度最大的手机型号为 T818,其次为 T92。手机各型号常见故障可如下表格所示。其中常见故障为开机故障、触屏故障、LCD 显示故障、通话故障，与上述的基于地区的手机常见故障的推荐所产生的结果相近，也表明了该品牌手机出现的故障与手机型号的差异关联性较小。同时观察下表，可以发现该结果与基于 Apriori 的型号与故障关联分析的结果存在差异，但是差异并不大。产生差异的原因主要是基于协同过滤的推荐算法考虑了各手机型号之间的相似性，产生了新的手机型号与故障之间关联。

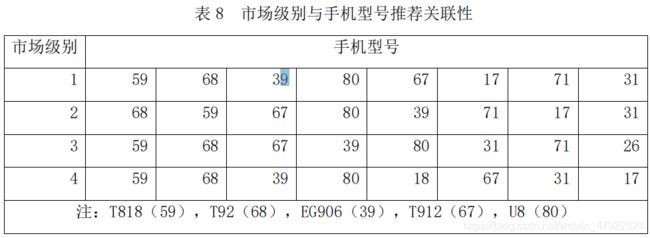
5）不同市场的常出故障的手机型号预测
结果分析：如下表所示，在不同级别的市场购买手机,，其出现故障较多的手机型号都是T818，T92，EG906，T912 和 U8 。综合上述地区与故障的关联分析及手机型号与故障的关联分析，为该设备生产企业的各地区服务点提供了备件需求预测。即该品牌手机常出现故障的手机型号为 T818，T92，EG906，T912 和 U8，而常见故障类型为开机故障、触屏故障、LCD 显示故障、通话故障，。同时图 3 已表明手机维修数据集中各省份各地区的维修记录数是存在差异的。设备生产企业需根据各地区的支持度大小及时向各地补 给这些种类的备件。

2.3.4 推荐算法的评价

（1）算法推荐质量评价方法的描述

推荐质量的评价标准有多种，做常用的是通过平均绝对偏差（MAE）对推荐质量进行评价。MAE 通过计算预测用户评分与实际的用户评分之间的偏差度量预测的准确性，MAE 越小，推荐质量越高。假设预测的用户的评分值合为{1, 2, ⋯ , },对应的实际评分集合为{1, 2, ⋯ , },则 MAE 可由下式计算：
$$MAE=\frac{{\sum }_{i=1}^N|p_i-q_i|}{N}$$

③

因为样本量比较大，只需随机将手机数据集按 4：1 的比例分训练集和测试集即可，准确性影响不大，本文使用 Clementine12.0 “分区”节点按 4:1 进行训练集和测试集分区。对测试集生成各地区与所有故障的评分反余弦矩阵 A，对训练集生成各地区与所有故障的预测评分反余弦矩阵Ｂ。根据公式③计算得到平均绝对偏差（MAE），MAE 越小代表推荐质量越高。由于评分矩阵的生成是根据数据集中记录条数，因此预测评分矩阵与实际评分矩阵在数值上存在差异，不可能得到 MAE=0。因此为了能显示出 MAE 的合理性，分别计算 A 和 B 的平均值和̅，通过比较 MAE 与、̅，若 M=|MAE-（+̅/4）|趋向于 0，即 M 越小代表推荐质量越高。

(2)推荐评价结果分析

运行程序（见附录 8），可算得 M=0.0732，M 接近于 0，因此由该推荐算法产生的推荐结果是比较理想的且可接受的。

3. 结论

本次数据挖掘目的是在维修记录信息进行归一化，区号提取等预处理的基础上，提取手机数据，采用数据挖掘技术，对产品型号、地区、市场级别与反映问题描述（故障）进行关联规则挖掘，基于协同过滤的个性推荐算法的手机数据集分析，从而推出备件的储备需求预测。

（1）由于原始的维修数据存在大量的噪声，后续工作的进行时十分不利的。可以通过其他属性来去除这些噪声数据的，如根据产品型号来填充价格（可认为同一牌子的同一型号的手机价格一样），但分析发现即使是同一牌子的同一型号的手机的价格也相差很远，因此很难替补。本文根据研究目的只选取手机数据集其中的五个属性进行分析，对于缺失数据只是进行简单的删除，因样本量大，故删除掉的少量数据对结果影响不大。

（2）通过利用基于协同过滤的个性推荐算法对手机数据集分析，可知在地理位置上相近的地区具有一定的关联性；不同的地区不同的手机型号常见的手机故障主要是开机故障，触屏故障，按键故障和通话故障，从而可得出备件的储备需求预测；在不同级别的市场购买的手机,，其经常出现故障的手机的手机型号都是 T818，T92，EG906，T912 和 U8，故可为消费者提供购买意见。

(3) 虽然用 Apriori 算法和 GRI 算法得到的模型的支持度或置信度不是很高，但是初步的结果跟用推荐算法得到的结果又一定的相似性，所以 Apriori 算法和 GRI 算法得到的结果可以算是本文粗略的结果，而推荐算法得到的是比较精确的结果。

4. 参考文献

[1] 薛薇.陈欢歌 Clementine 数据挖掘方法及应用 电子工业出版社

[2] 胡洁.张珂珩 数据挖掘在设备状态预测中的应用浅析 江苏瑞中数据股份有限公司

[3] 李卫斌 数据仓库和数据挖掘在航空维修信息分析中应用研究 2010.05

[4] 周张兰 基于协同过滤的个性化推荐算法研究 2009.06

[5] 刘 枚 莲 . 刘同存 . 李 小 龙 基 于 用 户 兴 趣 特 征 提 取 的 推 荐 算 法 研 究 1001-3695(2011)-05-1664-04

[6] 彭石 基于用户兴趣和项目特性的协同过滤推荐算法研究 2012.06

[7] 陶俊.张宁 基于用户兴趣分类的协同过滤推荐算法 2011

5. 附件

附录 1 手机故障及代号

附录 2 手机型号数值化程序

%%手机型号数值化
%
function Area()
clear all;clc;close all;
AREA=[];
[~,~,AREA]=xlsread('filename','Sheet1');
AREAsize=size(AREA,1); %数据的记录条数
type=AREA(2:AREAsize,3); %手机型号位于数据集中的第 3 列
area_type2=unique(type);
area_typesize2=size(area_type2,1);
area_type_type=subs(type,area_type2',{
     1:area_typesize2});
%将手机型号转换成数值型
xlswrite('Typedouble.xls',Typedouble); %保存矩阵
end

附录 3
地区对应数值化的数值表

附录 4
产品型号对应数值化的数值表

附录 5 地图及对应区号

附录 6 地区与故障的评分图

%%地区与故障的评分图 
function area_pro()
clear all;clc;close all;
A_P=xlsread(' holibour.xlsx','area_problem');
[line,col]=size(A_P);
x=1:col-1;
y=A_P(:,1);
 plot(x,[A_P(1,2:col)',A_P(2,2:col)',A_P(3,2:col)',A_P(4,2:col)',...
 A_P(5,2:col)',A_P(6,2:col)',A_P(7,2:col)',A_P(8,2:col)',...
 A_P(9,2:col)',A_P(10,2:col)',A_P(11,2:col)',A_P(12,2:col)'...
 A_P(13,2:col)',A_P(14,2:col)',A_P(15,2:col)',A_P(16,2:col)',...
 A_P(17,2:col)',A_P(18,2:col)',A_P(19,2:col)',A_P(20,2:col)'...
 A_P(21,2:col)',A_P(22,2:col)',A_P(23,2:col)',A_P(24,2:col)',...
 A_P(25,2:col)',A_P(26,2:col)',A_P(27,2:col)',A_P(28,2:col)',...
 A_P(29,2:col)',A_P(30,2:col)'])
 title('地区与故障');
end

附录 7 推荐算法的运行代码

%%
%推荐邻居矩阵
%
%Init 最原始地区与故障的概率矩阵
%Area_area 地区与地区的 cos 矩阵
%Problem 故障的描述
%%
%function result=tuijian()
clear all;clc;
[Init Area_area Problem]=CCOS();%维修设备的测试
neighbour=[];
DIST=0.7;
[line,col]=size(Init);
feel=Init(:,2:col); %去掉 Init 矩阵中的第一列（该列的数值代表服务商所在地 ）
[line,col]=size(feel);
feelmean=mean(feel,2) %求每行的平均值
for i=1:line
 for j=1:col
 sum=0;
 sumArea=0;
 for t=1:line
 if t~=i & Area_area(i,t)>=DIST
 sum=Area_area(i,t)*(feel(t,j)-feelmean(t))+sum;
 sumArea=Area_area(i,t)+sumArea;
 end
 end
 neighbour(i,j)=feelmean(i)+sum/sumArea;
 end
end
[vals,index]= sort(neighbour,2,'descend') ; %按行从大到小排列
%vals 排序后的距离
%index 之前的位置
F=Init(:,1);
for i=1:line
 result(i,:)=[F(i,1) Problem(index(i,:),1)'];%邻居矩阵
end
index=find(vals<=0);
result(index+line)=0;
%c=acos(neighbour);
%xlswrite('训练样本集.xlsx',c,'训练样本集'); %保存矩阵
xlswrite('holibour.xlsx',result,'推荐故障（cos>=0.8 ');
xlswrite('holibour.xlsx',vals,'推荐故障 cos 值'); %保存矩阵
%%
% %相近的邻居
% %余弦相似性
function [Feel holibour Problem]=CCOS()
clear all;clc
 [Feel Problem]=areaproblem();
[line,col]=size(Feel);
feel=Feel(:,2:col); %去掉 Feel 矩阵中的第一列（该列的数值代表服务商所在地 ）
[line,col]=size(feel);
feelst=feel';
for i=1:line
 NORM(i)=norm(feel(i,:));
end
holibour=(feel*feelst)./(NORM'*NORM); %余弦相似性计算公式
[vals,index]= sort(acos(holibour),2); %按行小到大排列
%vals 排序后的距离
%index 之前的位置
F=Feel(:,1);
for i=1:line

result(i,:)=[F(i,1) F(index(i,:),1)'];%邻居矩阵
end
result1=result;
result3=result;
index=find(vals>0.3);
result(index+line)=0;
index=find(vals>0.2);
result3(index+line)=0;
xlswrite('holibour.xlsx',result1,'邻居（不做处理）'); %保存矩阵
xlswrite('holibour.xlsx',result3,'邻居（cos>=0.8）');
xlswrite('holibour.xlsx',result,'邻居（cos>=0.7）');
xlswrite('holibour.xlsx',vals,'邻居 cos 值'); %保存矩阵
xlswrite('holibour.xlsx',holibour,'Area_area'); %保存矩阵
%%
%兴趣矩阵的生成
% % %%
function [area_problem area_type2]=areaproblem()
clear all;clc;close all;
global usetime market Area type problem
area_problem=[];
AREA=[];
[~,~,AREA]=xlsread('area.xlsx','Sheet1');
%[~,~,AREA]=xlsread('训练样本和测试样本.xlsx','测试样本集');%
% [~,~,AREA]=xlsread('训练样本和测试样本.xlsx','训练样本集');
AREAsize=size(AREA,1); %数据的记录条数
for i=1:AREAsize-1
usetime(i,1)=AREA{
     i+1,1}; %使用时长 数值型
market (i,1)=AREA{
     i+1,2}; %市场级别 数值型
Area (i,1)=AREA{
     i+1,4}; %服务商所在地 数值型
type (i,1)=AREA{
     i+1,6}; %手机型号数值型
problem (i,1)=AREA{
     i+1,7}; %反映问题描述 数值型
end
area_type1=unique(Area);
area_type2=unique(problem);

area_typesize1=size(area_type1,1);
area_typesize2=size(area_type2,1);
area_problem=zeros(area_typesize1,area_typesize2+1); %服务商所在地 、型号相关矩阵
weixiutime=25-usetime;
area_problem(:,1)=area_type1;
for a=1:area_typesize1
 for p=2:area_typesize2+1
 sum=0;
 for i=1:AREAsize-1
 if Area(i)==area_type1(a) & problem(i)==area_type2(p-1)
 sum=sum+weixiutime(i);
 end
 end 
 area_problem(a,p)=sum; 
 end
end
[line col]=size(area_problem);
%c=acos(area_problem(:,2:col));
%xlswrite('测试样本集.xlsx',c,'测试样本集');
% xlswrite('训练样本集.xlsx',area_problem,'area_problem');
附录 8
%%
%%%误差验证
%fact 实际矩阵
%result 预测矩阵
function WEA()
clear all;clc;
fact=xlsread('测试样本集.xlsx','测试样本集');
result=xlsread('训练样本集.xlsx','训练样本集');
[line,col]=size(fact);
A=mean(mean(fact));
B=mean(mean(result));
M=0;

for i=1:line
 sum=0;
 for j=1:col
 sum=abs(fact(i,j)-result(i,j))+sum;
 end
 M=sum/col+M;
end
M=abs(M/line-A-B/4)