JavaScript数据结构与算法总结三——树(二叉搜索树、平衡树:AVL树&红黑树)
文章目录
- 树
-
- 二叉树
- 平衡树
-
- AVL树
- 红黑树
树
二叉树
树,它对于存储需要快速查找的数据非常有用。树是一种分层数据的抽象模型。
中的每个元素都叫作节点,节点分为内部节点和外部节点。位于树顶部的节点叫作根节点,它没有父节点。树至少有一个子节点的节点称为内部节点。没有子元素的节点称为外部节点或叶节点。
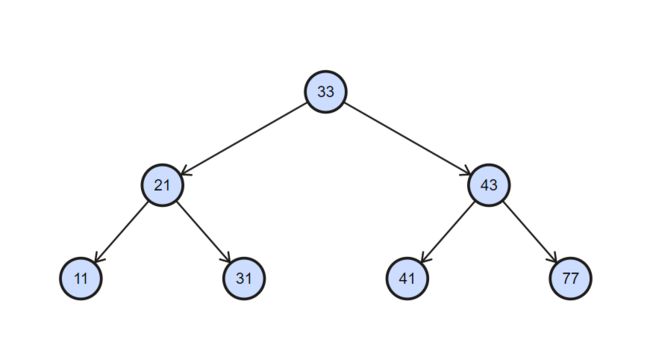
二叉搜索树(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值。
有三种遍历 BST 的方式:中序、先序和后序。中序遍历按照节点上的键值,以升序访问 BST 上的所有节点。先序遍历先访问根节点,然后以同样方式访问左子树和右子树。后序 遍历先访问叶子节点,从左子树到右子树,再到根节点。
//树节点
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
function show() {
return this.data; }
function BST() {
this.root = null;
this.insert = insert;//增
this.preOrder = preOrder;//先序遍历
this.inOrder = inOrder;
this.postOrder = postOrder;
this.getMin = getMin;//查
this.getMax = getMax;//查
this.find = find;
this.remove=remove;//删除
}
function insert(data) {
var n = new Node(data, null, null);
if (this.root == null) {
this.root = n;
} else {
var current = this.root; var parent;
while (true) {
parent = current;
if (data < current.data) {
current = current.left;
if (current == null) {
parent.left = n; break;
}
} else {
current = current.right;
if (current == null) {
parent.right = n; break;
}
}
}
}
}
//先序遍历
function preOrder(node) {
if (!(node == null)) {
document.write(node.show(), " ");
preOrder(node.left);
preOrder(node.right);
}
}
//中序遍历
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left);
document.write(node.show(), " ");
inOrder(node.right);
}
}
//后序遍历
function postOrder(node) {
if (!(node == null)) {
postOrder(node.left);
postOrder(node.right);
document.write(node.show(), " ");
}
}
//查找最小值
function getMin() {
var current = this.root;
while (!(current.left == null)) {
current = current.left;
}
return current.data;
}
//查找最大值
function getMax() {
var current = this.root;
while (!(current.right == null)) {
current = current.right;
} return current.data;
}
//查找值
function find(data) {
var current = this.root;
while (current != null) {
if (current.data == data) {
return current;
} else if (data < current.data) {
current = current.left;
} else {
current = current.right; }
}
return null;
}
//删除
function remove(data) {
root = removeNode(this.root, data);
}
function removeNode(node, data) {
if (node == null) {
return null; }
if (data == node.data) {
// 没有子节点的节点
if (node.left == null && node.right == null) {
return null; }// 没有左子节点的节点
if (node.left == null) {
return node.right; }// 没有右子节点的节点
if (node.right == null) {
return node.left; }// 有两个子节点的节点
var tempNode = getSmallest(node.right);
node.data = tempNode.data;
node.right = removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) {
node.left = removeNode(node.left, data);
return node;
} else {
node.right = removeNode(node.right, data);
return node;
}
}
var testTree = new BST();
testTree.insert(33);
testTree.insert(21);
testTree.insert(43);
testTree.insert(11);
testTree.insert(31);
testTree.insert(41);
testTree.insert(77);
document.write("preOrder traversal: ");
preOrder(testTree.root);
document.write("
Inorder traversal: ");
inOrder(testTree.root);
document.write("
postOrder traversal: ");
postOrder(testTree.root);
let min = testTree.getMin();
document.write("
The minimum value of the BST is: ", min);
let max = testTree.getMax();
document.write("
The maximum value of the BST is: ", max);
let value = 11;
if (testTree.find(value)) {
document.write("
Found ", value, " in the BST.");
} else {
document.write("
", value, " was not found in the BST.");
}
平衡树
BST 存在一个问题:取决于你添加的节点数,树的一条边可能会非常深;也就是说,树的一
条分支会有很多层,而其他的分支却只有几层,这会在需要在某条边上添加、移除和搜索某个节点时引起一些性能问题。
AVL 树是一种自平衡二叉搜索树,意思是任何一个节点左右两侧子树的高度之差最多为 1。
| 类型 | 平衡度 | 调整频率 | 适用场景 |
|---|---|---|---|
| AVL树 | 高 | 高 | 查询多,增/删少 |
| 红黑树 | 低 | 低 | 增/删频繁 |
AVL树
AVL树是一种自平衡树。添加或移除节点时,AVL树会尝试保持自平衡。任意一个节点(不论深度)的左子树和右子树高度最多相差 1。添加或移除节点时,AVL树会尽可能尝试转换为完全树。
在 AVL 树中插入或移除节点和 BST 完全相同。然而,AVL 树的不同之处在于我们需要检验它的平衡因子,如果有需要,会将其逻辑应用于树的自平衡。
如果在向左侧子树插入节点后树不平衡了,我们需要比较是否插入的键小于左侧子节点的键。如果是,我们要进行 LL 旋转。否则,要进行 LR 旋转。
如果在向右侧子树插入节点后树不平衡了,我们需要比较是否插入的键小于右侧子节点的键。如果是,我们要进行 RR 旋转。否则,要进行 RL 旋转。
//AVL树
function AVLTreeNode(data, left, right) {
this.data = data;
this.left = null;
this.right = null;
this.parent = null;
this.show = show;
}
function show() {
return this.data; }
function AVLTree() {
var root = null;
this.insert = insert; //插入
this.preOrder = preOrder;//先序遍历
this.inOrder = inOrder;
this.postOrder = postOrder;
this.getMin = getMin;//最小
this.getMax = getMax;//最大
this.find = find;//按值查找
this.compareFn = compareFn;//比较两个数据元素
}
function compareFn(data1, data2) {
if (data1 === data2) {
return 0;
} else if (data1 < data2) {
return -1;
} else {
return 1;
}
}
//insert:向树中插入一个新的节点
function insert(data) {
var node = new AVLTreeNode(data, null, null);
if (this.root == null) {
this.root = node;
} else {
let current = this.root; let parent;
while (true) {
parent = current;
if (data < current.data) {
current = current.left;
if (current == null) {
parent.left = node; break;
}
} else {
current = current.right;
if (current == null) {
parent.right = node; break;
}
}
}
this.root = balanceNode(this.root, data);//对树进行调整
}
}
//平衡左右子树
function balanceNode(node, data) {
// 如果需要,将树进行平衡操作
const balanceFactor = this.getBalanceFactor(node);
if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
if (this.compareFn(data, node.left.data) === Compare.LESS_THAN) {
node = this.rotationLL(node);
} else {
return this.rotationLR(node);
}
}
if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
if (
this.compareFn(data, node.right.data) === Compare.BIGGER_THAN
) {
node = this.rotationRR(node);
} else {
return this.rotationRL(node);
}
}
return node;
}
//获取高度
function getNodeHeight(node) {
if (node == null) {
return -1;
}
return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}
//获取树的平衡因子
function getBalanceFactor(node) {
const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
switch (heightDifference) {
case -2:
return BalanceFactor.UNBALANCED_RIGHT;
case -1:
return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
case 1:
return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
case 2:
return BalanceFactor.UNBALANCED_LEFT;
default:
return BalanceFactor.BALANCED;
}
}
//避免处理平衡因子的数值
const BalanceFactor = {
UNBALANCED_RIGHT: 1,
SLIGHTLY_UNBALANCED_RIGHT: 2,
BALANCED: 3,
SLIGHTLY_UNBALANCED_LEFT: 4,
UNBALANCED_LEFT: 5
};
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1
};
//左-左(LL型):向右的单旋转
function rotationLL(node) {
let temp = node.left;
node.left = temp.right;
temp.right = node;
return temp;
}
//右-右(RR型):向左的单旋转
function rotationRR(node) {
let temp = node.right;
node.right = temp.left;
temp.left = node;
return temp;
}
//左-右(LR型,左侧子节点的高度大于右侧子节点的高度,并且左侧子节点右侧较重):向右的双旋转(左旋-右旋)
function rotationLR(node) {
node.left = this.rotationRR(node.left);
return this.rotationLL(node);
}
//右-左(RL型):向左的双旋转(右旋-左旋)
function rotationRL(node) {
node.right = this.rotationLL(node.right);
return this.rotationRR(node);
}
//先序遍历
function preOrder(node) {
if (!(node == null)) {
document.write(node.show(), " ");
preOrder(node.left);
preOrder(node.right);
}
}
//中序遍历
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left);
document.write(node.show(), " ");
inOrder(node.right);
}
}
//后序遍历
function postOrder(node) {
if (!(node == null)) {
postOrder(node.left);
postOrder(node.right);
document.write(node.show(), " ");
}
}
//查找最小值
function getMin() {
var current = this.root;
while (!(current.left == null)) {
current = current.left;
}
return current.data;
}
//查找最大值
function getMax() {
var current = this.root;
while (!(current.right == null)) {
current = current.right;
} return current.data;
}
//查找值
function find(data) {
var current = this.root;
while (current != null) {
if (current.data == data) {
return current;
} else if (data < current.data) {
current = current.left;
} else {
current = current.right; }
}
return null;
}
var testTree = new AVLTree();
testTree.insert(77);
testTree.insert(41);
testTree.insert(31);
testTree.insert(43);
testTree.insert(33);
testTree.insert(11);
testTree.insert(21);
document.write("preOrder traversal: ");
preOrder(testTree.root);
document.write("
InOrder traversal: ");
inOrder(testTree.root);
document.write("
postOrder traversal: ");
postOrder(testTree.root);
let min = testTree.getMin();
document.write("
The minimum value of the BST is: ", min);
let max = testTree.getMax();
document.write("
The maximum value of the BST is: ", max);
let value = 11;
if (testTree.find(value)) {
document.write("
Found ", value, " in the BST.");
} else {
document.write("
", value, " was not found in the BST.");
}
红黑树
顾名思义,每个节点不是红的就是黑的;
(2) 树的根节点是黑的;
(3) 所有叶节点都是黑的(用 NULL 引用表示的节点);
(4) 如果一个节点是红的,那么它的两个子节点都是黑的;
(5) 不能有两个相邻的红节点,一个红节点不能有红的父节点或子节点;
(6) 从给定的节点到它的后代节点(NULL 叶节点)的所有路径包含相同数量的黑色节点
//红黑树
function RedBlackNode(key) {
this.data = key;
this.left = null;
this.right = null;
this.parent = null;
this.color = Colors.RED;
this.show = show;
this.isRed=isRed;
}
const Colors = {
RED: 0,
BLACK: 1
};
function isRed() {
return this.color === Colors.RED;
}
function RBTree() {
var root = null;
this.insert = insert; //插入
this.insertNode = insertNode;
this.fixTreeProperties = fixTreeProperties;
this.rotationRR=rotationRR;
this.rotationLL=rotationLL;
this.preOrder = preOrder;//先序遍历
this.inOrder = inOrder;
this.postOrder = postOrder;
this.getMin = getMin;//最小
this.getMax = getMax;//最大
this.find = find;//按值查找
this.compareFn = compareFn;//比较两个数据元素
}
function show() {
return this.data; }
//插入数据
function insert(key) {
if (this.root == null) {
//如果没有根节点则直接加入根节点
this.root = new RedBlackNode(key);
this.root.color = Colors.BLACK;
} else {
var node = this.insertNode(this.root, key);
}
this.fixTreeProperties(node);
}
function insertNode(node, key) {
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
if (node.left == null) {
node.left = new RedBlackNode(key);
node.left.parent = node;
return node.left;
}
else {
return this.insertNode(node.left, key);
}
}
else if (node.right == null) {
node.right = new RedBlackNode(key);
node.right.parent = node;
return node.right;
}
else {
return this.insertNode(node.right, key);
}
}
function fixTreeProperties(node) {
while (node && node.parent && node.parent.isRed() // 验证它的父节点是否是红色
&& node.color !== Colors.BLACK) {
// 验证这个节点是否不是黑色
let parent = node.parent; // 保存父节点
const grandParent = parent.parent; // 保存祖父节点
// 父节点是左侧子节点
if (grandParent && grandParent.left === parent) {
const uncle = grandParent.right;
if (uncle && uncle.color === Colors.RED) {
grandParent.color = Colors.RED;
parent.color = Colors.BLACK;
uncle.color = Colors.BLACK;
node = grandParent;
}
else if (node === parent.right) {
// 节点是右侧子节点——左旋转
this.rotationRR(parent); // {12}
node = parent;
parent = node.parent;
} else {
// 节点是左侧子节点——右旋转
this.rotationLL(grandParent);
parent.color = Colors.BLACK;
grandParent.color = Colors.RED;
node = parent;
}
}
else {
// 父节点是右侧子节点
const uncle = grandParent.left;
// 叔节点是红色——只需要重新填色
if (uncle && uncle.color === Colors.RED) {
// {10}
grandParent.color = Colors.RED;
parent.color = Colors.BLACK;
uncle.color = Colors.BLACK;
node = grandParent;
} else if (node === parent.left) {
// 节点是左侧子节点——右旋转
this.rotationLL(parent); // {19}
node = parent;
parent = node.parent;
}
else {
//节点是右侧子节点——左旋转
this.rotationRR(grandParent); // {20}
parent.color = Colors.BLACK;
grandParent.color = Colors.RED;
node = parent;
}
}
}
this.root.color = Colors.BLACK; // {11}
}
function rotationLL(node) {
const tmp = node.left;
node.left = tmp.right;
if (tmp.right && tmp.right.key) {
tmp.right.parent = node;
}
tmp.parent = node.parent;
if (!node.parent) {
this.root = tmp;
}
else {
if (node === node.parent.left) {
node.parent.left = tmp;
}
else {
node.parent.right = tmp;
}
}
tmp.right = node;
node.parent = tmp;
}
function rotationRR(node) {
const tmp = node.right;
node.right = tmp.left;
if (tmp.left && tmp.left.key) {
tmp.left.parent = node;
}
tmp.parent = node.parent;
if (!node.parent) {
this.root = tmp;
}
else {
if (node === node.parent.left) {
node.parent.left = tmp;
}
else {
node.parent.right = tmp;
}
}
tmp.left = node;
node.parent = tmp;
}
function compareFn(data1, data2) {
return data1 < data2 ? Compare.LESS_THAN : Compare.BIGGER_THAN
}
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1
};
//先序遍历
function preOrder(node) {
if (!(node == null)) {
document.write(node.show(), " ");
preOrder(node.left);
preOrder(node.right);
}
}
//中序遍历
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left);
document.write(node.show(), " ");
inOrder(node.right);
}
}
//后序遍历
function postOrder(node) {
if (!(node == null)) {
postOrder(node.left);
postOrder(node.right);
document.write(node.show(), " ");
}
}
//查找最小值
function getMin() {
var current = this.root;
while (!(current.left == null)) {
current = current.left;
}
return current.data;
}
//查找最大值
function getMax() {
var current = this.root;
while (!(current.right == null)) {
current = current.right;
} return current.data;
}
//查找值
function find(data) {
var current = this.root;
while (current != null) {
if (current.data == data) {
return current;
} else if (data < current.data) {
current = current.left;
} else {
current = current.right; }
}
return null;
}
var testTree = new RBTree();
testTree.insert(77);
testTree.insert(41);
testTree.insert(31);
testTree.insert(43);
testTree.insert(33);
testTree.insert(11);
testTree.insert(21);
document.write("preOrder traversal: ");
preOrder(testTree.root);
document.write("
InOrder traversal: ");
inOrder(testTree.root);
document.write("
postOrder traversal: ");
postOrder(testTree.root);
let min = testTree.getMin();
document.write("
The minimum value of the BST is: ", min);
let max = testTree.getMax();
document.write("
The maximum value of the BST is: ", max);
let value = 11;
if (testTree.find(value)) {
document.write("
Found ", value, " in the BST.");
} else {
document.write("
", value, " was not found in the BST.");
}