KMP算法

看这个视频就好啦

https://www.youtube.com/watch?v=dgPabAsTFa8&t=3s

and this article:

http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/

http://www.cnblogs.com/zhangtianq/p/5839909.html

字符串匹配问题：

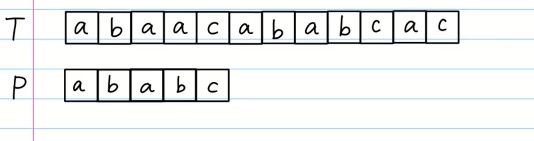
暴力解法

发现没匹配成功，移动短的P string

，

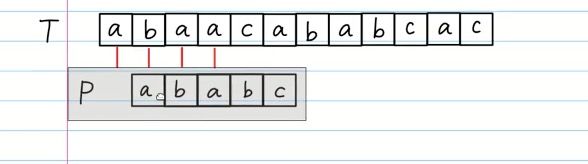
KMP

先写出prefix table，准确说叫 相同前后缀Table。

在哪个位置匹配不上，按照prefix table上的index，把string 的index对准匹配失败的地方。

Edit on July 31. 

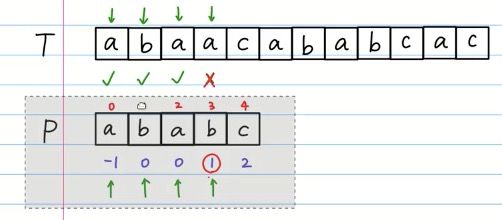
有一个地方要非常注意，KMP算法中当有一个字符对不上的时候，查看的是prefix table里position j-1位置上的value。然后把pattern[value]对其第一个对不上的地方。花了很多时间一直在看这个例子以后我终于知道为什么work了，而且为什么是position j-1！

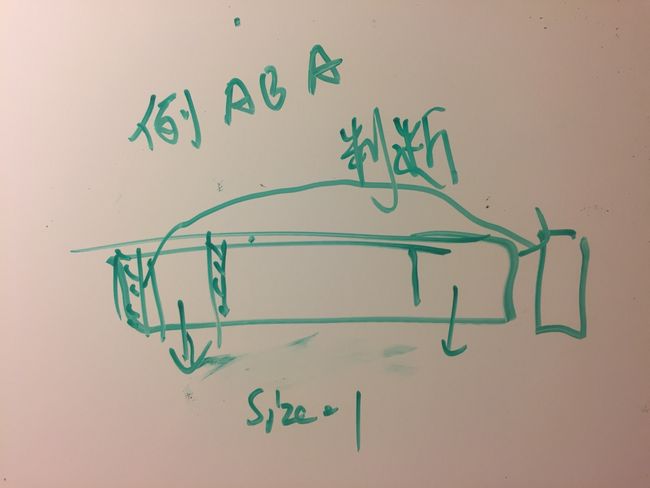
首先当 abaa 和abab对不上的时候，暴力解法是只把abab往右移动一位。但是KMP会移动两位，因为已经知道ab和ab是完全一样的。所以要怎么理解position j-1? 我的理解是，如果b和a对不上，那这个时候就应该看b前一个的字母的最长相同前后缀的长度了。 比如abaa 和abab. 没对上的前一个字母是a。 其实我们已经知道最后一个字母b前面所有字母之前都和text完全一一对应了。我们现在想让失败的case前几个字母要和Text对上.

The worst case complexity of Naive algorithm is O(m(n-m+1)). 因为最多要move entire string向右一格 n-m+1 次。 每次要对比m个字符。 

 Time complexity of KMP algorithm is O(n) in worst case.  n > m.

lps[i] = the longest proper prefix of pat[0..i]

which is also a suffix of pat[0..i].

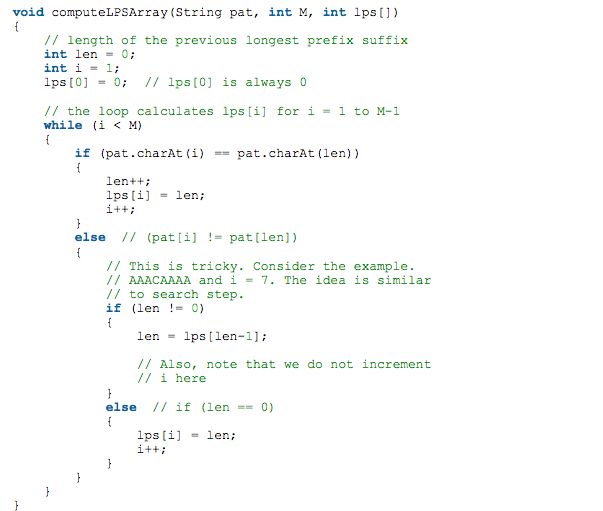
Preprocessing 那一步是最难的, 研究半天发现 这个就是DP的思想来求的。

Examples of lps[] construction:

For the pattern “AAAA”,

lps[] is [0, 1, 2, 3]

这里的k 这个数代表的是previous longest prefix. 这个真的很难理解！

为什么要判断k>-1, 以及ndl[k+1] != ndl[i]?

首先明确一下最长前后缀的意思： 就是前面跟屁股一样。abacaba 前面和后面一样aba。

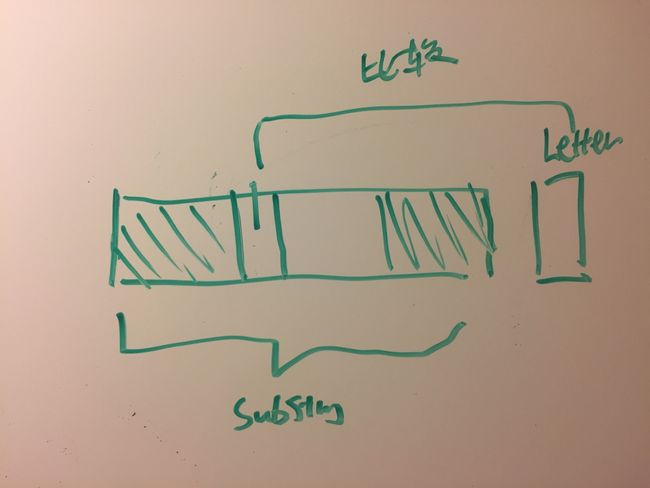
看下图： 我们假设以及求出前一个substring的最长前后缀，到现在这个现在新的letter的位置。我们想知道有没有可能整个string的前面， 跟尾巴【包含letter】是相等的，相等的话，最长前后缀就会在之前的基础上加一。

判断k>-1是因为如果之前的最长前后缀<=-1, 根本都没有过最长前后缀呢！

如果不相等的话，我们找到position为前一个最长前后缀那么大的地方开始，然后看看这个substring的最前半部分的下一个letter跟当前这个letter有没有一样。一样的话好歹我们的最长前后缀还能有一点东西不至于为0.  为什么取从position为前一个最长前后缀那么大的地方开始? 因为

首先前半部分跟后半部分是一样的，通过之前已知。也就是前半部分substring里的的最长前缀跟后半部分的最长后缀一样！所以我们想在这个基础上看看最后一个letter有没有办法组成更长的。

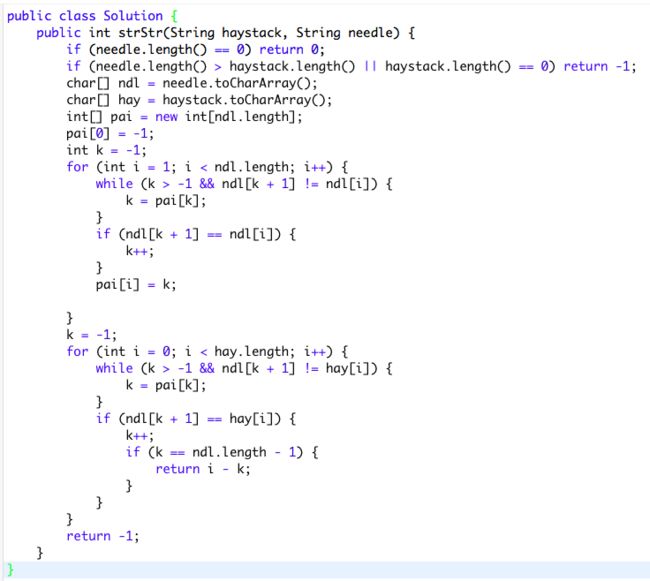
练习KMP的两道题1. strStr()    2. shortest Palindrome.

Edit on 8月12号凌晨

今天重新回顾KMP，又发现新知识。。。之前其实并没有理解KMP为什么要做一个Prefix Table.

Table里的每一个位置其实是str 从0到index位置的这个subproblem的最长前后缀的值。【也可以移动一格】。比如说abab，假设我们只看到aba 这个单词，他的最长前后缀是1. a 和a

假设我们看到abab，这个最长前后缀是0. 

但是比如 abaa和abab，b最后一个字母不match，我们要把第二个string的index 1的letter b对准abaa的index 3. 因为index 3是mismatch的地方。 之前的已经确认完全一样。又因为aba 这个subproblem的最长前后缀为1. 所以第一个字母a和最后一个字母a确定是一样的。所以可以把aba的第一个字母移动到aba的最后一个字母a的位置，也就导致了aba的b对准了abaa之前mismatch的position 3. 

这就是为什么我们要求出每个子substring的最大前后缀。