字符串匹配的KMP算法详解及C#实现

字符串匹配是计算机的基本任务之一。

　　举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"？许多算法可以完成这个任务，Knuth-Morris-Pratt算法（简称KMP）是最常用的之一。它以三个发明者命名，起头的那个K就是著名科学家Donald Knuth。

      这种算法不太容易理解，网上有很多解释，但读起来都很费劲。直到读到Jake Boxer的文章，我才真正理解这种算法。下面，我用自己的语言，试图写一篇比较好懂的KMP算法解释。

      1.

　　首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

　　2.

　　因为B与A不匹配，搜索词再往后移。

　　3.

　　就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

　　4.

　　接着比较字符串和搜索词的下一个字符，还是相同。

　　5.

　　直到字符串有一个字符，与搜索词对应的字符不相同为止。

　　6.

　　这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

　　7.

　　一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

　　8.

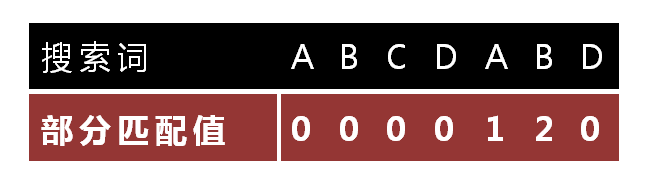
　　怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

　　9.

　　已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值

　　因为 6 - 2 等于4，所以将搜索词向后移动4位。

　　10.

　　因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

　　11.

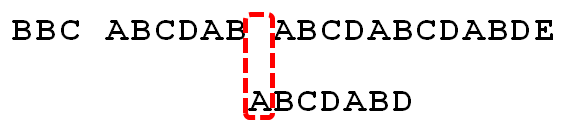
　　因为空格与A不匹配，继续后移一位。

　　12.

　　逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

　　13.

　　逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

　　14.

　　下面介绍《部分匹配表》是如何产生的。

　　首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

　　15.

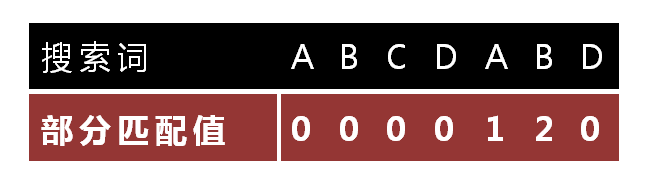
　　"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

　　16.

　　"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

以上 KMP算法的分析 原文地址：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

下面是我用C#实现上述分析：

 

 1         /// <summary>

 2         /// KMP算法查找字符串

 3         /// </summary>

 4         /// <param name="operateStr">操作字符串</param>

 5         /// <param name="findStr">要查找的字符串</param>

 6         /// <returns>字符串第一次出现的位置索引</returns>

 7         public static int Arithmetic_KMP(string operateStr, string findStr)

 8         {

 9             int index = -1;   //正确匹配的开始索引

10             int[] tableValue = GetPartialMatchTable(findStr);

11             int i = 0, j = 0; //操作字符串和匹配字符串 索引迭代

12             while (i < operateStr.Length && j < findStr.Length)

13             {

14                 if (operateStr[i] == findStr[j]) //当第一个字符匹配上，接着匹配第二、、、

15                 {

16                     if (j == 0) index = i;       //记录第一个匹配字符的索引

17                     j++;

18                     i++;

19                 }

20                 else  //当没有匹配上的时候

21                 {

22                     if (j == 0) //如果第一个字符就没匹配上

23                     {

24                         i += j + 1 - tableValue[j]; //移动位数 =已匹配的字符数 - 对应的部分匹配值

25                     }

26                     else

27                     {

28                         i = index + j - tableValue[j - 1]; //如果已匹配的字符数不为零，则重新定义i迭代

29                     }

30                     j = 0; //将已匹配迭代置为0

31                 }

32             }

33             return index;

34         }

35         /// <summary>

36         /// 产生 部分匹配表

37         /// </summary>

38         /// <param name="str">要查找匹配的字符串</param>

39         /// <returns></returns>

40         public static int[] GetPartialMatchTable(string str)

41         {

42             string[] left, right; //前缀、后缀

43             int[] result = new int[str.Length]; //保存 部分匹配表

44             for (int i = 0; i < str.Length; i++)

45             {

46                 left = new string[i]; //实例化前缀 容器

47                 right = new string[i]; //实例化后缀容器

48                 //前缀

49                 for (int j = 0; j < i; j++)

50                 {

51                     if (j == 0)

52                         left[j] = str[j].ToString();

53                     else

54                         left[j] = left[j - 1] + str[j].ToString();

55                 }

56                 //后缀

57                 for (int k = i; k > 0; k--)

58                 {

59                     if (k == i)

60                         right[k - 1] = str[k].ToString();

61                     else

62                         right[k - 1] = str[k].ToString() + right[k];

63                 }

64                 //找到前缀和后缀中相同的项，长度即为相等项的长度（相等项应该只有一项）

65                 int num = left.Length - 1;

66                 for (int m = 0; m < left.Length; m++)

67                 {

68                     if (right[num] == left[m])

69                     {

70                         result[i] = left[m].Length;

71                     }

72                     num--;

73                 }

74             }

75             return result;

76         }

View Code

 

如果要查询出匹配字符串出现的所有位置，可以使用递推来循环查找，代码如下：

 1         /// <summary>

 2         /// 尾递归查询出 字符串出现的所有开始索引 

 3         /// </summary>

 4         /// <param name="str1">操作字符串</param>

 5         /// <param name="str2">要查找的字符串</param>

 6         /// <param name="indexs">位置索引 集合</param>

 7         public static void Search(string str1, string str2, IList<int> indexs)

 8         {

 9             int index = Arithmetic_KMP(str1, str2);

10             int temp = index;

11             if (indexs.Count > 0)

12             {

13                 index += indexs[indexs.Count - 1] + str2.Length;

14             }

15             indexs.Add(index);

16             if (temp + (str2.Length - 1) * 2 <= str1.Length)

17                 Search(str1.Substring(temp + str2.Length), str2, indexs);

18         }

View Code

这是我看了KMP算法解析后，用C#代码实现的。如有不足之处，请指出，谢谢！还有其他朋友的实现，代码如下：

 1         private static int KmpIndexOf(string s, string t)

 2         {

 3             int i = 0, j = 0, v;

 4             int[] nextVal = GetNextVal(t);

 5 

 6             while (i < s.Length && j < t.Length)

 7             {

 8                 if (j == -1 || s[i] == t[j])

 9                 {

10                     i++;

11                     j++;

12                 }

13                 else

14                 {

15                     j = nextVal[j];

16                 }

17             }

18 

19             if (j >= t.Length)

20                 v = i - t.Length;

21             else

22                 v = -1;

23 

24             return v;

25         }

26 

27 

28 

29         private static int[] GetNextVal(string t)

30         {

31             int j = 0, k = -1;

32             int[] nextVal = new int[t.Length];

33 

34             nextVal[0] = -1;

35 

36             while (j < t.Length - 1)

37             {

38                 if (k == -1 || t[j] == t[k])

39                 {

40                     j++;

41                     k++;

42                     if (t[j] != t[k])

43                     {

44                         nextVal[j] = k;

45                     }

46                     else

47                     {

48                         nextVal[j] = nextVal[k];

49                     }

50                 }

51                 else

52                 {

53                     k = nextVal[k];

54                 }

55             }

56 

57             return nextVal;

58         }

View Code

 

这种实现比我上面的实现，性能要高出三倍，原因在与，它生成“Next特征数组”（网上有资料这么叫的）只用了一个循环，而我的用了三个循环，貌似最后那个数组值也不一样，没看懂他的思路是怎么回事，如有懂的，请指点下，谢谢！测试代码下载：http://files.cnblogs.com/joey0210/ArithmeticSolution.rar