Pytorch和Tensorflow在相同数据规模规模下的降维PCA(Principal Component Analysis)算法中的运算速度对比
Pytorch和Tensorflow在相同数据规模规模下的降维PCA(Principal Component Analysis)算法中的运算速度对比
在网上找了好久都没找到pytorch使用特征值与特征向量实现pca算法的教程(即非svd算法),本文中的代码是根据个人对pca的理解所写的,致敬开源思想,将学习过程与程序放在这里,希望对大家有帮助,共同学习,共同进步(不喜勿喷)
PCA算法基本原理
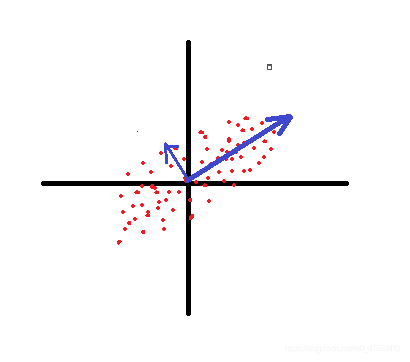
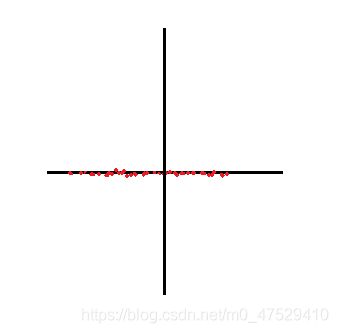
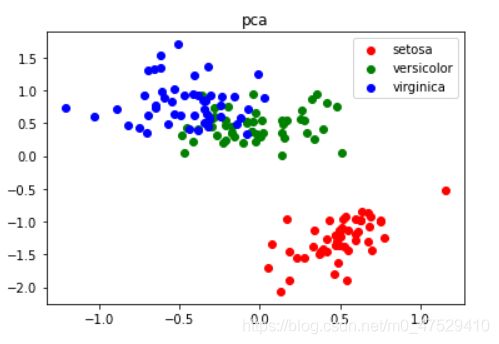
PCA的基本原理是从大量的数中找到少数主要的成分点,在数据维度降低的情况下尽可能地保存原始数据的信息。举个例子:假设有一个二维的数据,其分布如下面第一个图所示,蓝色粗箭头的方向就是第一个轴的方向(即离散程度最高大 方差最大),这就意味着数据点在蓝色粗线上的投影代表了原始数据的绝大部分信息。所以我们将蓝色的两条轴作为新的轴(两条蓝轴正交),然后将所有数据点沿着第二轴往第一轴投影,得到第三张图的数据分布。
协方差
我们知道我们知道数值的分散程度,可以用数学上的协方差来表述。协方差可以表示两个变量之间的相关性。如果协方差为0那么就说明这两个变量之间是不相关的。否侧他们相关。协方差公式为:
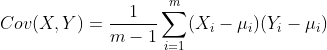
这时我们让均值为 0,那么就变为:
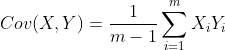
为了让协方差为 0,我们选择第二个基时只能在与第一个基正交的方向上进行选择,因此最终选择的两个方向一定是正交的。
X = ( a 1 a 2 … … a i b 1 b 2 … … b i ) X=\begin{pmatrix} a_1 & a_2 & …… & a_i\\\\ b_1 & b_2 & …… & b_i\\\\ \end{pmatrix} X=⎝⎜⎜⎛a1b1a2b2…………aibi⎠⎟⎟⎞
那么:
1 m − 1 X X T = ( 1 m − 1 ∑ i = 1 m a i 2 1 m − 1 ∑ i = 1 m a i b i 1 m − 1 ∑ i = 1 m a i b i 1 m − 1 ∑ i = 1 m b i 2 ) \frac{1}{m-1}XX^T=\begin{pmatrix} \frac{1}{m-1}\sum_{i=1}^{m}a_{i}^2 & \frac{1}{m-1}\sum_{i=1}^{m}a_ib_{i} \\\\ \frac{1}{m-1}\sum_{i=1}^{m}a_ib_{i} & \frac{1}{m-1}\sum_{i=1}^{m}b_{i}^2 \\\\ \end{pmatrix} m−11XXT=⎝⎜⎜⎛m−11∑i=1mai2m−11∑i=1maibim−11∑i=1maibim−11∑i=1mbi2⎠⎟⎟⎞
= ( C o v ( a , a ) C o v ( a , b ) C o v ( a , b ) C o v ( b , b ) ) =\begin{pmatrix} Cov(a,a) & Cov(a,b)\\\\ Cov(a,b) &Cov(b,b) \\\\ \end{pmatrix} =⎝⎜⎜⎛Cov(a,a)Cov(a,b)Cov(a,b)Cov(b,b)⎠⎟⎟⎞
此时我们要主对角线以外的数都为0那么我们假设 C = 1 m − 1 X X T C= \frac{1}{m-1}XX^T C=m−11XXT而设最终结果的矩阵为P那么设我们要的变换后的结果为Y=PX,D为Y的协方差矩阵
D = 1 m − 1 Y Y T = 1 m − 1 P X ( P X ) T D = \frac{1}{m-1} YY^T = \frac{1}{m-1}PX(PX)^T D=m−11YYT=m−11PX(PX)T
= 1 m − 1 P X X T P T = P ( 1 m − 1 X X T ) P T = P C P T = \frac{1}{m-1} PXX^TP^T = P(\frac{1}{m-1}XX^T)P^T =PCP^T =m−11PXXTPT=P(m−11XXT)PT=PCPT
那么我们只要求出C的特征向量和特征值就可以了,我们所需要的是最大的k(k为降维后的维度)个特征值对应的特征向量。
代码实现(使用的CPU为锐龙R5-3500U)
pytorch实现
iris数据集下
import torch
import numpy as np
import time
from sklearn import datasets
import matplotlib.pyplot as plt
data = datasets.load_iris(return_X_y=False)
def pca(x,dim=2):
m,n=x.shape[0],x.shape[1]
#print(m,n)
X=torch.from_numpy(x)
#去中心化 防止数据过分逼近大的值 而忽略小的值
X_mean = torch.mean(X,0)
X=X-X_mean.expand_as(X)
# 无偏差的协方差矩阵
cov = torch.matmul(X.T,X)/(m - 1)
#print(cov)
# 计算特征分解
e,v = torch.eig(cov,eigenvectors=True)
#print(e)
#print(v.shape[0])
e=torch.mean(e,1)*2
#print(e)
# 将特征值从大到小排序,选出前dim个的index
sorted, e_index_sort = torch.sort(e,descending=True)
e_index_sort=torch.gather(e_index_sort,-1,torch.LongTensor([0,1]))
v_new = torch.index_select(v, 0, e_index_sort)
#print(v_new)
# 降维操作
pca = torch.matmul(X,v_new.T)
return(pca)
#运行代码
start = time.perf_counter()
pca_data = pca(data.data,dim=2)
elapsed = (time.perf_counter()-start)
print(f'time use :{elapsed}')
#可视化
Y= data.target
pca = pca_data.numpy()
plt.figure()
color=['red','green','blue']
for i, target_name in enumerate(data.target_names):
plt.scatter(pca[Y==i,0],pca[Y==i,1],label = target_name, color = color[i])
plt.legend()
plt.title('pca')
plt.show
自定义10000*1000数据规模下
import torch
import numpy as np
import time
from sklearn import datasets
import matplotlib.pyplot as plt
n0=2*np.random.randn(5000,1000)+1
n1=-2*np.random.randn(5000,1000)-1
n=np.vstack((n0,n1))
def pca(x,dim=2):
m,n=x.shape[0],x.shape[1]
#print(m,n)
X=torch.from_numpy(x)
#去中心化 防止数据过分逼近大的值 而忽略小的值
X_mean = torch.mean(X,0)
X=X-X_mean.expand_as(X)
# 无偏差的协方差矩阵
cov = torch.matmul(X.T,X)/(m - 1)
#print(cov)
# 计算特征分解
e,v = torch.eig(cov,eigenvectors=True)
#print(e)
#print(v.shape[0])
e=torch.mean(e,1)*2
#print(e)
# 将特征值从大到小排序,选出前dim个的index
sorted, e_index_sort = torch.sort(e,descending=True)
e_index_sort=torch.gather(e_index_sort,-1,torch.LongTensor([0,1]))
v_new = torch.index_select(v, 0, e_index_sort)
#print(v_new)
# 降维操作
pca = torch.matmul(X,v_new.T)
return(pca)
#运行代码
start = time.perf_counter()
pca_data = pca(data.data,dim=2)
elapsed = (time.perf_counter()-start)
print(f'time use :{elapsed}')
tensorflow实现
iris数据集下
import tensorflow.compat.v1 as tf
# 使用Eager Execution动态图机制
tf.enable_eager_execution()
import numpy as np
from sklearn import datasets
import seaborn as sns
import matplotlib.pyplot as plt
import time
data = datasets.load_iris(return_X_y=False)
def pca(x,dim = 2):
'''
x:输入矩阵
dim:降维之后的维度数
'''
with tf.name_scope("PCA"):#创建一个参数名空间
m,n= tf.to_float(x.get_shape()[0]),tf.to_int32(x.get_shape()[1])
assert not tf.assert_less(dim,n)
mean = tf.reduce_mean(x,axis=0)
# 去中心化 防止数据过分逼近大的值 而忽略小的值
x_new = x - mean
# 无偏差的协方差矩阵
cov = tf.matmul(x_new,x_new,transpose_a=True)/(m - 1)
#print(cov)
# 计算特征分解
e,v = tf.linalg.eigh(cov,name="eigh")
#print(e)
#print(v)
# 将特征值从大到小排序,选出前dim个的index
e_index_sort = tf.math.top_k(e,sorted=True,k=dim)[1]
#print(e_index_sort)
# 提取前排序后dim个特征向量
v_new = tf.gather(v,indices=e_index_sort)
#print(v_new)
# 降维操作
pca = tf.matmul(x_new,v_new,transpose_b=True)
return pca
start = time.perf_counter()
pca_data = tf.constant(np.reshape(data.data,(data.data.shape[0],-1)),dtype=tf.float32)
pca_data = pca(pca_data,dim=2)
elapsed = (time.perf_counter()-start)
print(f'time use :{elapsed}')
Y= data.target
pca = pca_data.numpy()
plt.figure()
color=['red','green','blue']
for i, target_name in enumerate(data.target_names):
plt.scatter(pca[Y==i,0],pca[Y==i,1],label = target_name, color = color[i])
plt.legend()
plt.title('pca')
plt.show
![]()
算法中的运算速度对比_第5张图片](http://img.e-com-net.com/image/info8/50703e9ee0e2462aa138f64eab44b1c8.jpg)
自定义10000*1000数据规模下
import tensorflow.compat.v1 as tf
# 使用Eager Execution动态图机制
tf.enable_eager_execution()
import numpy as np
from sklearn import datasets
import seaborn as sns
import matplotlib.pyplot as plt
import time
n0=2*np.random.randn(5000,1000)+1
n1=-2*np.random.randn(5000,1000)-1
n=np.vstack((n0,n1))
def pca(x,dim = 2):
'''
x:输入矩阵
dim:降维之后的维度数
'''
with tf.name_scope("PCA"):#创建一个参数名空间
m,n= tf.to_float(x.get_shape()[0]),tf.to_int32(x.get_shape()[1])
assert not tf.assert_less(dim,n)
mean = tf.reduce_mean(x,axis=0)
# 去中心化 防止数据过分逼近大的值 而忽略小的值
x_new = x - mean
# 无偏差的协方差矩阵
cov = tf.matmul(x_new,x_new,transpose_a=True)/(m - 1)
#print(cov)
# 计算特征分解
e,v = tf.linalg.eigh(cov,name="eigh")
#print(e)
#print(v)
# 将特征值从大到小排序,选出前dim个的index
e_index_sort = tf.math.top_k(e,sorted=True,k=dim)[1]
#print(e_index_sort)
# 提取前排序后dim个特征向量
v_new = tf.gather(v,indices=e_index_sort)
#print(v_new)
# 降维操作
pca = tf.matmul(x_new,v_new,transpose_b=True)
return pca
start = time.perf_counter()
pca_data = tf.constant(np.reshape(data.data,(data.data.shape[0],-1)),dtype=tf.float32)
pca_data = pca(pca_data,dim=2)
elapsed = (time.perf_counter()-start)
print(f'time use :{elapsed}')
![]()
因为pca算法在计算的过程中运算量并不大,所以两个架构在执行该算法的时候时间相差并不大,但是也可以看出在不同的数据集下,两个框架运算速度不同,说明数据对框架运算速度起到很大的影响。同时不同数据下可以看出tensorflow的效果更好(以上为个人观点,不喜勿喷)