高斯勒让德数值积分公式
高斯勒让德数值积分公式
- 1 引言
- 2 高斯积分公式
-
- 2.1 一维区间上高斯数值积分公式
- 2.2 二维三角形上的高斯数值积分公式
1 引言
在数值求解微分方程的时候,例如利用有限元方法求解微分方程时,经常会遇到计算给定区域上的积分的问题。 在实际问题中,由于被积函数以及积分区域的复杂性,通常采用数值方法进行求解。在插值型积分公式中,高斯积分公式具有最高的代数精度,所以是常用的数值积分公式。
2 高斯积分公式
2.1 一维区间上高斯数值积分公式
区间 [ a , b ] [a,b] [a,b]上带权函数的插值型数值积分公式的一般形式为
∫ a b ρ ( x ) f ( x ) d x ≈ ∑ i = 0 n A i f ( x i ) : = I n \int^b_a\rho(x)f(x)dx\approx\sum^n_{i=0}A_if(x_i):=I_n ∫abρ(x)f(x)dx≈i=0∑nAif(xi):=In
其中 x i ( i = 0 , 1 , 2 , ⋯ , n ) x_i(i=0,1,2,\cdots,n) xi(i=0,1,2,⋯,n)称为插值节点。
这里我们需要先介绍下代数精度的概念。
定义(代数精度)若数值积分公式 I n = ∑ i = 0 n A i f ( x i ) I_n=\sum^n_{i=0}A_if(x_i) In=∑i=0nAif(xi) 对 m m m次多项式精确成立,并且存在一个 m + 1 m+1 m+1次多项式,使得数值积分公式不精确成立,则称该数值积分公式的代数精度为 m m m.
由于连续函数可以由多项式函数一致逼近,我们可以认为代数精度越高的数值积分公式,近似效果越好。对于有 n + 1 n+1 n+1个节点的数值积分公式 I n I_n In, 通过恰当地选择节点 x i x_i xi和系数 A i A_i Ai, 能使 I n I_n In的代数精度达到 2 n + 1 2n+1 2n+1. 如果 I n I_n In的代数精度为 2 n + 1 2n+1 2n+1,那么称 I n I_n In为高斯数值积分公式。在这里集中讨论 ρ ( x ) = 1 \rho(x)=1 ρ(x)=1的情况,相应的数值积分公式为高斯勒让德积分公式。
现在的问题是如何得到高斯积分公式的积分节点 x i x_i xi和系数 A i A_i Ai。直接利用高斯公式的代数精度为 2 n + 1 2n+1 2n+1,求解关于 x i , A i x_i, A_i xi,Ai的非线性方程组
∫ a b x k d x = ∑ i = 0 n A i x i k , k = 0 , 1 , 2 , ⋯ , 2 n + 1 (1) \int^b_ax^kdx=\sum^n_{i=0}A_ix^k_i, k=0,1,2,\cdots,2n+1 \tag{1} ∫abxkdx=i=0∑nAixik,k=0,1,2,⋯,2n+1(1)
是非常困难的。 但是幸运的是,可以证明正交多项式的零点高斯积分公式的积分节点(称为高斯点),所以可以先通过正交多项式的零点,得到高斯点 x i x_i xi, 此时(1)式变为关于 A i A_i Ai的线性方程组,从而很容易求出。
我们知道勒让德多项式是区间 [ − 1 , 1 ] [-1,1] [−1,1]上的正交多项式,我们首先要将区间 [ a , b ] [a,b] [a,b]上的积分化为 [ − 1 , 1 ] [-1,1] [−1,1]上。这并不困难,通过变换
x = b − a 2 t + a + b 2 x=\frac{b-a}{2}t+\frac{a+b}{2} x=2b−at+2a+b
即可。勒让德多项式 P n + 1 ( x ) P_{n+1}(x) Pn+1(x)的零点即是数值积分公式(2)
∫ − 1 1 f ( x ) d x ≈ ∑ i = 0 n A i f ( x i ) (2) \int^1_{-1}f(x)dx\approx\sum^n_{i=0}A_if(x_i)\tag{2} ∫−11f(x)dx≈i=0∑nAif(xi)(2)
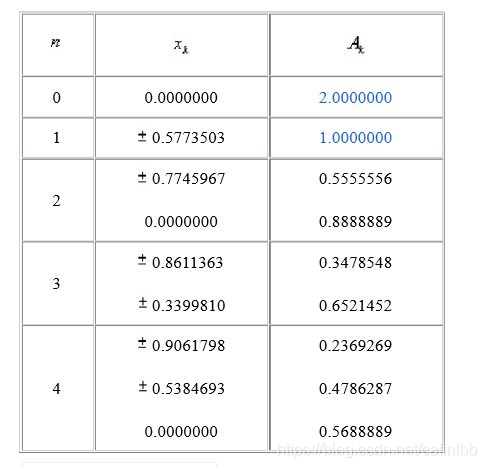
的高斯点。低阶的高斯勒让德积分公式的节点和系数如下表所示:(图片截自百度文库https://wenku.baidu.com/view/a767f6878762caaedd33d4f4.html)
2.2 二维三角形上的高斯数值积分公式
对于任意的三角形 K K K,总是可以通过面积坐标,将其映射到一个标准的三角形 K ^ \hat{K} K^, 如图所示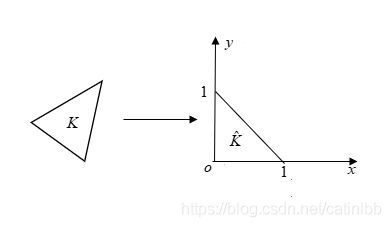
所以下面我们仅讨论在 K ^ \hat{K} K^上的高斯积分公式。显然有
I = ∫ K ^ f ( x , y ) d x d y = ∫ 0 1 d x ∫ 0 1 − x f ( x , y ) d y I=\int_{\hat{K}}f(x,y)dxdy=\int^1_0dx\int^{1-x}_0f(x,y)dy I=∫K^f(x,y)dxdy=∫01dx∫01−xf(x,y)dy
做变量替换 u = x , v = y 1 − x u=x, v=\frac{y}{1-x} u=x,v=1−xy, 则有 0 ≤ u , v ≤ 1 0\leq u,v\leq 1 0≤u,v≤1, ∂ ( x , y ) ∂ ( u , v ) = 1 − u \frac{\partial(x,y)}{\partial(u,v)}=1-u ∂(u,v)∂(x,y)=1−u, 那么
I = ∫ 0 1 ∫ 0 1 f ( u , ( 1 − u ) v ) ( 1 − u ) d u d v I=\int^1_0\int^1_0f(u,(1-u)v)(1-u)dudv I=∫01∫01f(u,(1−u)v)(1−u)dudv
进一步做变换
u = 1 + ξ 2 , v = 1 + η 2 u=\frac{1+\xi}{2}, v=\frac{1+\eta}{2} u=21+ξ,v=21+η
则有 − 1 ≤ ξ , η ≤ 1 -1\leq \xi,\eta\leq 1 −1≤ξ,η≤1, ∂ ( u , v ) ∂ ( ξ , η ) = 1 4 \frac{\partial(u,v)}{\partial(\xi,\eta)}=\frac{1}{4} ∂(ξ,η)∂(u,v)=41, 现在有
I = ∫ − 1 1 ∫ − 1 1 f ( 1 + ξ 2 , ( 1 − ξ ) ( 1 + η ) 4 ) 1 − ξ 8 d ξ η I=\int^1_{-1}\int^1_{-1}f(\frac{1+\xi}{2},\frac{(1-\xi)(1+\eta)}{4})\frac{1-\xi}{8}d\xi\eta I=∫−11∫−11f(21+ξ,4(1−ξ)(1+η))81−ξdξη
现在我们已经将积分区域映射到 [ − 1 , 1 ] × [ − 1 , 1 ] [-1,1]\times[-1,1] [−1,1]×[−1,1], 这样三角形上的积分就化为 [ − 1 , 1 ] [-1,1] [−1,1]上的二重积分,从而可以利用一维高斯积分公式做计算。
参考资料
1.《计算方法》,孙文瑜,杜其奎,陈金如. 科学出版社.
2. H. T. Rathod, K. V. Nagaraja, B. Venkatesudu and N. L. Ramesh, “Gauss Legendre quadrature over a triangle”. J. Indian Inst. Sci., Sept.–Oct. 2004, 84, 183–188.