哈希表查找
1.什么是哈希表(Hash Tables)
哈希表可以以极快的速度来查找、添加或删除元素(只需要数次的比较操作。)由于查找的时候不需要比较,所以它比二分查找、红黑树、二叉搜索树都要快得多。但是哈希表没有排序功能,类似的,如寻找最大值、最小值、中值这些行为都不能在哈希表中实现。
2.实现哈希表的前提条件
要想对一组元素做成哈希表形式的数据结构,这些元素需要满足两个条件:
A. 元素拥有自己的哈希值。
B. 两个元素可以判断出是否相等。
第二个条件比较容易实现,关键是第一个条件。在介绍哈希表前,将先介绍哈希值。
3. 什么是哈希值(hash code)
哈希值是一个int类型的整数。每个元素都应该有自己的哈希值,并且这个值是唯一的。即满足:
A. 如果元素a与元素b相等,则元素a的哈希值与元素b的哈希值相等。
B. 如果元素a与元素b不相等,则元素a的哈希值与元素b的哈希值不相等。
通常情况下,对于int,bool,double,string等语言自带的类型都有自己的哈希值,可以用它们的哈希函数来获取,不同语言的哈希函数可能会不同。
如果是用户自己新建的类型,则需要提供计算此类型元素哈希值的哈希函数。
在哈希表中,我们是通过某元素的哈希值来查找、添加或删除元素的。
3.1哈希冲突:
对于某个哈希函数的两个关键码K1,K2。如果K1!=K2 而 Hash(K1)=Hash(K2),则称出现了哈希冲突,
处理冲突的办法就是为出现冲突的关键码找到一个“空”的哈希地址
4. 如何实现哈希表
有许多方法可以实现哈希表,这里将介绍两种:拉链法 和 开放地址法。
5. 拉链法(separate chaining)
从例子入手:
现有整数类型(int)的数组S:7,30,10,9,14,19,15,12,90,94,93,53,70。此数组的元素的哈希值与元素值相同,即7的哈希值是7;30的哈希值是30。
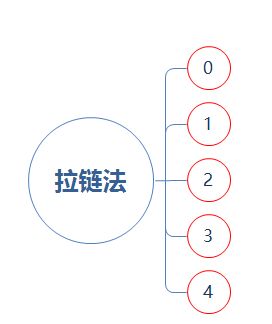
现创建一个有5个元素的数组A:(红色颜色只是为了与数组S的元素区分开来)
然后按顺序把数组S插入数组A中:
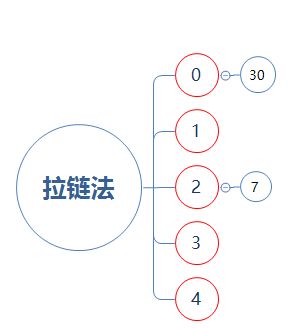
插入元素7:元素7的哈希值为7,7%5=2,因此插入到2号元素中;
插入元素30:元素30的哈希值为30,30%5=0,因此插入到0号元素中;
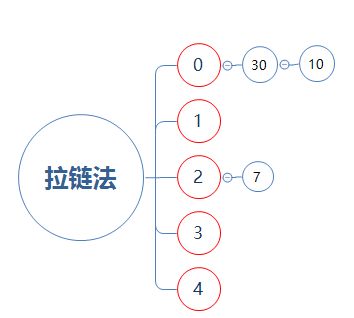
插入元素10:元素10的哈希值为10,10%5=0,因此插入到0号元素中,但0号元素已经有数值30了,故插到30后面,元素30的指针指向元素10。
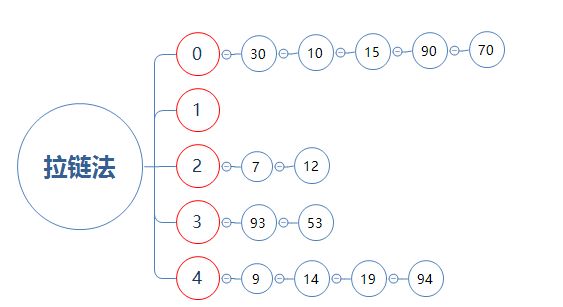
如此类推,插入元素9:元素9的哈希值为9,9%5=4,因此插入到4号元素中...
全部元素添加完毕后:
现在,如果我们要查找元素19:
元素19的哈希值为19,19%5=4,因此到4号元素去找;
4号元素的值为9,9!=19,去找9的指针指向的元素14;
14!=19,去找14的指针指向的元素19;
19==19,返回数值,查找完毕。
此过程只经历了3次比较!
从此例子中可以看出思路:
对于一个拥有N项元素的数组S,我们需要建立一个含有M项元素的新数组A。
M的值可以自己来定,但如果M过大,则会出现很多空链,如上述例子中的1号链;
如果M过小,则会出现链太长的情况,如果链太长,则意味着比较次数变多。
一般建议M=N/5。
插入元素:
int j=S[i]的哈希值%5;
然后检查A[j]是否为空,如果空,A[j]=S[i]; 如果不为空,temp=A[j], A[j]=S[i], S[i].next=temp;
删除元素:先找出该元素,然后此元素的上一个元素的指针指向此元素的下一个元素,最后删除此元素。
拉链法有一个缺陷,就是很容易有些链过长,有些链过短,甚至是空链。这样会浪费内存和影响搜索速度。
6. 开放定址法(Open Addressing)
一旦产生了冲突(该地址已有其它元素),就按某种规则去寻找另一空地址
若发生了第 i 次冲突,试探的下一个地址将增加di,基本公式是:
Hi= (Hash(key)+di) % m ( 1≤ i < TableSize )
Hash(key)为哈希函数,di为增量序列,m为哈希表的表长
di 决定了不同的解决冲突方案:线性探测、平方探测、双散列。
线性探测:di = i
平方探测:di = ± i^2
双散列:di = i * h2(key)
6.1线性探测法
从例子入手:
现有整数类型(int)的数组S:7,30,10,9,14,19,15,29,13,27。此数组的元素的哈希值与元素值相同,即7的哈希值是7;30的哈希值是30。
现创建一个含有14个元素的数组A:(上面那排数字是为了方便看哪个元素是第几项元素)
然后按顺序把数组S插入数组A中:
插入元素7:元素7的哈希值为7,7%14=7,因此插入到7号元素中;
插入元素30:元素30的哈希值为30,30%14=2,因此插入到2号元素中;
插入元素10:元素10的哈希值为10,10%14=10,因此插入到10号元素中;
插入元素9:元素9的哈希值为9,9%14=9,因此插入到9号元素中;
插入元素14:元素14的哈希值为14,14%14=0,因此插入到0号元素中;
插入元素19:元素19的哈希值为19,19%14=5,因此插入到5号元素中;
插入元素15:元素15的哈希值为15,15%14=1,因此插入到1号元素中;
插入元素29:元素29的哈希值为29,29%14=1,但1号元素已经有数值15了,然后检查下一个元素(2号元素),但2号元素已经有数值30了,然后检查下一个元素(3号元素),3号元素为空,插入到3号元素:
插入元素13:元素13的哈希值为13,13%14=13,因此插入到13号元素中:
插入元素27:元素27的哈希值为27,27%14=13,但13号元素已经有数值13了,然后检查下一个元素(0号元素),但0号元素已经有数值14了,如此类推,找到4号元素为空,插入到4号元素:
如果我们要查找元素29,元素29的哈希值为29,29%14=1,检查1号元素,15!=29;然后检查下一个元素(2号元素),30!=29;然后检查下一个元素(3号元素),29=29,返回数值,查找完毕。
从此例子中可以看出思路:
对于一个拥有N项元素的数组S,我们需要建立一个含有M项元素的新数组A。
M一定要比N大。如果M过少,则搜索进行的比较次数增加,影响速度;如果过大,则太多空位没利用,造成内存浪费。
一般建议M=2*N。
插入元素i: 先获取i的哈希值%M,根据这个值插入到相应的位置中,如果位置有元素了,则插入到下一个位置,循环进行,直到位置是空的为止。
搜索元素:类似于插入元素,详细见上述例子。