从0搞懂递归(1)——递归入门详解

一、前言

     递归是一个老生常谈的问题，可能在大一学习C语言的时候大家就开始接触了递归。而后又在数据结构、算法等课程中频频涉及。相信很多人和我一样，对递归的理解也是一步步加深，这种感觉很难说出来。每每有人问起，如何理解递归。我只能说，多读递归，多看递归等……却没有建设性的建议。最近比较闲，我就在思考，为什么大家都能看懂斐波那契数列的递归，却看不懂树图遍历、汉诺塔、DFS呢？我尝试从0出发，尽力讲一个0基础能够听懂的递归。这个系列大概会有两到三篇文章，不断的深入讨论递归。像往常一样声明，本文纯干货，都是自己的理解，希望读者可以认认真真体会每一句话，读完后一定有收获。当然，能力一般水平有限，如果有问题欢迎指正，如果觉得说的不错，麻烦点个赞。【未经允许，请勿转载】

二、什么是递归（已经能够熟练写出斐波那契等简单递归的请跳过）

     递归函数是什么呢？一句话，一个函数在运行的时候调用了自身，这就是递归函数。

void function ()
{
printf("Hello World");
function();
}

上述代码中的function函数运行到第二行又调用了他自己，这就是一个递归函数。相信点开这个博文的小伙伴们肯定是看懂了阶乘、斐波那契的代码。

int fact(int n){//定义阶乘函数
	if(n==1) return 1;//输入的参数是1，直接返回1
	else return n*fact(n-1);//递归算法
}
int main(){
int x;
x = f(3);
printf("%d",x);
}

以阶乘这个代码为例，下图的黄色箭头指向了代码运行的方向，蓝色表示运行的顺序。

一个程序从主函数开始运行，运行到1（1表示蓝色数字1对应箭头的代码片段）的末尾时候（x=f（3））我们需要通过调用f（）函数才能得到x的值，故我们进入f函数传入参数n=3也就是箭头2。进入f函数按照箭头3的顺序开始运行，由于n的值是3并不是1直接运行到这个函数的最后一行，也就是return n*fact（n-1）。由于这个n传入的值为3也就是我们return的结果是3*fact（2）。这时候我们发现并不知道fact（2）是多少，我们又要需要重复调用fact这个函数，并且传入参数n=2（也就是执行箭头4）。同样的情况按照箭头5的代码执行到函数最后一个行我们fact（2）的结果是2*fact（1）。我们又需要得到fact（1）所以需要再次进行fact的调用，这次传参n=1（箭头6）。由于n=1，代码段执行到7的时候符合if的判定标准直接return 1；这时候我们就知道了fact（1） = 1代码向箭头8走；fact（2） = 2*fact（1）中的fact（1）也得出了结果所以fact（2） = 2*1 = 2；这时候执行箭头9，fact（3） = 3*fact（2）也就是6.我们得到了fact（3）的结果后直接返回给主函数的x。这时候x成功赋值，再执行十一行，成功打印x。可以看看下面这张图有助理解。

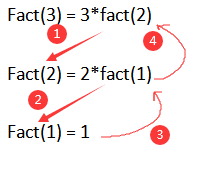相信看过这一阶段的同学们对最基本的递归有了较浅的理解了，那我们继续深入讨论。

三、从斐波那契到打印型的递归“函数”

        第二节所讲的知识，相信90%的同学都能够熟练掌握，这一节才算真正的开始讨论递归这个问题，像树的先序遍历等递归中嵌入printf从而实现函数功能的代码很多，相信大家也都是这块有很多疑问。我把他们统称为打印型的递归函数。如果你现在的情况是如下我提出的，建议从这一节开始读，否则跳到第四节。现在你的情况是不是这样？

我能够熟练看懂斐波那契数列等利用函数做递推式的问题了。
因为这些问题往往有明确的函数我可以把第n层到n+1层找到关系。
但是碰到打印型比如树的先序遍历，我勉勉强强能看懂，再难我就费劲了。

   如果你是这上述情况，那么需要进一步提升读懂递归代码的能力，如果不是，可以直接看下一节，转变思想来写递归。

对于打印型的递归函数不能理解，主要是有两个问题。

1）递归的执行过程是“递”与“归”，理解了不断调用，也就是“递”的过程，也要着眼于“递”结束后，每个函数还要“归”来执行没有执行完的部分。

2）不要沉浸在画一个图或者画一个树，然后逐步验证递归的思维之中。

本节将要围绕着两点具体的分析，先上一个代码。

#include
void f(int x)
{
    if(x==0)
    {printf("C ");
    return;}
    printf("A%d ",x);
    f(x-1);
    printf("B%d ",x);
}

int main()
{
    f(3);
}

这个代码执行后输出的结果如下：。不知道和大家思考的结果是否一样。经过上一节的训练相信大家至少能写出他的输出是A3 A2 A1 C；可能有些人想不明白为什么B1,B2,B3是倒序输出的呢？这个还要回归第二节所讲的内容，我们来看如下图所示，该程序的执行顺序。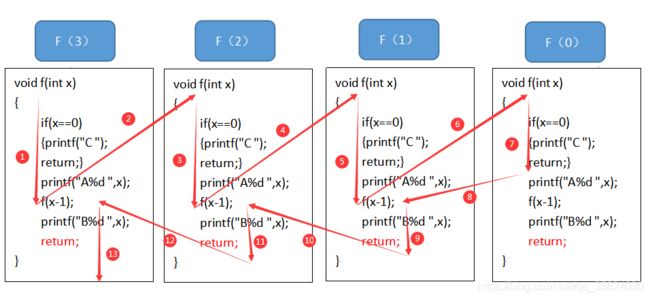

有这么几点需要注意，当每个函数执行到结尾，表明这个函数执行完成，自动return。所以我在每个函数末尾加了一个return便于理解。箭头1与箭头13中打印的x的值为3；箭头3与箭头11中打印的x的值为2；箭头5与箭头9中打印的x的值为1；箭头7中由于x值为0，打印字符C。相信这个图大家都能看懂，也就明白了为什么要打印A3 A2 A1 C B1 B2 B3。我们回过头来分析一下，为什么B1,B2,B3会与A3,A2,A1反序输出呢？因为我们在调用下一层的递归结束之后，还要返回本层继续执行没有执行完成的代码。这个回来继续执行的过程就是“归”的过程。大多数初学者往往注意了“递”的过程，而总是没有把“归”的过程考虑清楚。我们在调用的时候是从左向右调用即一次调用f(3)->f(2)->f(1)，也就是打印A3,A2,A1；调用f(0)后，f(0)是一个转折点，也就是所谓的递归出口（下一节会详叙）f(0)中由于x是0，没有按照平时的路线去执行这个函数，而是打印了一个C字符后直接返回。注意！现在要把没有执行完的部分执行完！也就是所谓递归的“归”。这个归是从右向左归来的。所以一次是完成f(1)->f(2)->f(3)没有执行完的部分，也就是打印B1,B2,B3。到这里，入门的递归懂了一半，现学现用来看看二叉树的中遍历的代码

void inorder(Node* &root)
{
if(root==NULL)
    return;//如果该结点是空，返回
inorder(root->leftChild);//访问左孩子
printf("%d",root->data);//打印当前结点的值
inorder(root->rightChild);//访问右孩子
}

前两行就类似于我们上一个例子的f(0)，就是让递归的“递”到达终点，转向“归”的临界点。也就是所谓的递归出口。

下面这三行也和刚才的例子类似，我们先去中序遍历该结点的左子树，再打印当前值，再遍历该结点的右子树。大家可以在纸上自己画一下类似我上方画的程序执行顺序图。是不是可以理解这个为什么对了？BUT。相信大家虽然知道这个程序为什么是正确的了，但是还是没有那种通透的感觉，这就要看我在这一节开头所提到的第二条内容：不要把自己的思维沉浸在验证递归中。说到底，如果我们画一个二叉树，看看哪个结点被执行了，哪个结点没有执行。我们还是没有摆脱开迭代的思想。我们还是试图用迭代的思想来理解递归。这个东西说起来容易，做起来难。我尽力把我的思路分析给大家，需要大家慢慢消化。

以这个先序遍历二叉树的例子为例。我们要做的不应该是：

啊这个结点先被执行了；这个结点已经到叶子结点了，打印！；然后递归往上返回！然后打印！；递递递递递！归归归归归！

这么做是不对的=。=！但是我们刚才说的这个阶段又是我们必须经历的。当我们多次推导，已经发现推了一个又一个但是再看新的还是不能一眼通透更不要说自己写的时候。就会渐渐有另一个思路：递归——定义一个规则，和一个出口，忽略其中的细节。以这个二叉树的中序遍历为例。首先这个递归的出口是什么呢？就是这个结点左右都没孩子了就该遍历它自己就结束了对吧？再来看函数的主体由于我打印自己夹在左儿子和右儿子中间。所以我可以保障的是，左子树全遍历完才能归来，才能打印我自己的值，然后再打印我的右子树。换句话说，左子树的所有结点都会在我之前打印，右子树都会在我之后打印。wocao？这不就是中序遍历的定义吗？？先遍历我左子树，再遍历我自己，然后遍历我右子树。（这块读者可以停下来慢慢琢磨一下，比较一下和以前迭代思维的不同）。如果后续时间充裕，我会在此再补充几个例子，大家看完上面这个例子。再去读读我这一节所说的那两句话。是不是感觉对递归清楚了很多呢？这块需要自己多消化消化。希望很多读者读到这已经有所收获。那么我们下一步就是自己能不能尝试写递归呢？或者说有些题你能不能想到可以用递归做呢？如果能写好递归，代码简单可读性又高（其他性能问题再后续讨论）开发时间又短。下一节我们就要详细的说说递归的三要素，说说怎么写递归。

三、递归函数的三要素

     这一节讲会讲述如何写出一个递归函数（不考虑写出来的递归的性能，即是否有重复结点是否高效等问题，这部分会在后续章节讲解）。首先要明确递归的三要素：

第一，函数式的功能：你首先要明确每一次执行F（x）你做什么事情。

第二，递归出口，也就是我们上文所说到的“递”的结束，“归”的开始。

第三，递推式，或者说程序的逻辑，如阶乘中的F（n）=n*F（n-1），如中序遍历的先左子树、再遍历自己、后遍历右子树。

在做一个递归函数时候，最重要的是考虑好第一点。这一次递归，你要干什么。执行一次递归函数基本上是迭代方法中的一次循环，也就是说做一次原子性的操作（比如遍历一个结点）。递归往往会与分治的思想同时用到。分治思想就是把一个大的问题划分为几个规模小的问题来解决。分治加递归就是不断的分化，把一个整体的问题分而治之。怎么分是第3要素要解决的。分到哪停是第2要素要解决的，而每一个东西做什么这是第1要素要解决的。这个也是最重要的。 

第二点要素递归出口是标志着一个程序的递归转折点，这个往往是很容易设计出来的，但是要注意的是这个判定要放置在整个函数的最开始，每次进入递归先进行递归出口的判定，否则会进入不断递归的死循环。

第三点递推式与设计，这是递归的难点。我们要充分结合上一节所讲到的思想。不要考虑整个程序具体的每一步如何执行，而是要设计好规则。

还是以中序遍历为例。首先想这个函数式的功能是什么呢？是遍历一个结点对吗？注意是1，这是原子性的体现。有些问题不好这个动作，要好好体会。这个函数大概的功能我知道了，遍历一个结点，然后引出别的结点加入遍历。那么遍历到哪里结束呢？应该是遍历到叶子结点吧？因为没法再往下遍历了。好了，最后结束函数如何设计递推式、程序的逻辑了，中序遍历是要先遍历左子树，再遍历我自己，再遍历右子树对吗?所以很明显，由本节点，递归调用f(本节点的左节点)和f(本节点的右结点)，这个思路是没问题的。可是这两个函数放在哪呢？由于先遍历左子树，不难想象f(本节点的左节点)应该放在“递”的过程中，也就是遍历自己之前，而f(本节点的右节点)，应该放在“归”的过程中，也就是放在遍历自己之后。这个代码就很容易的写出来了。参考这个例子，我相信所有树、图的遍历问题基本也就没有什么问题了，而且你会发现，很多平常练习的小题目，也可以用这种思维多去练习自己去写

四、暂时的结语

   本节主要是提供了想问题的思路，大家还是要多加动手练习啊~学到这，大家应该能写出一个简单的递归，那么，递归在系统中是如何实现的呢（递归栈）？递归就这么完美吗（开销巨大）？我们如何写出更优秀更高效的递归代码呢（尾递归）？面对更加复杂的递归问题，我们又应该做怎样的思考呢？欲知后事如何，点个关注，点个赞啊，后面会及时更新！！