VLSI数字信号处理系统——第十三章位级运算架构
VLSI数字信号处理系统——第十三章位级运算架构
作者:夏风喃喃
参考:
(1) VLSI数字信号处理系统:设计与实现 (美)Keshab K.Parhi/著
(2) socvista https://wenku.baidu.com/u/socvista?from=wenku
文章目录
- VLSI数字信号处理系统——第十三章位级运算架构
-
- 一. 引言
- 二. 并行乘法器
-
- 2.1 具有符号扩展的并行乘法
-
- 2.1.1 并行(串行进位)阵列乘法器
- 2.1.2 并行(进位保留)阵列乘法器
- 2.2 Baugh-Wooley乘法器
- 2.3 改进的Booth重编码并行乘法器
- 三. 交织布局规则与基于位平面的数字滤波器(略)
- 四. 位串行乘法器
-
- 4.1 利用Horner法则的Lyon位串行乘法器的设计
- 4.2 利用脉动映射的位串行乘法器的设计
- 五. 位串行滤波器的设计与实现
-
- 5.1 位串行FIR滤波器
- 5.2 位串行IIR滤波器
- 六. 正则符号数运算
-
- 6.1 CSD表示法
- 6.2 CSD乘法
- 七. 分布式运算(略)
-
- 7.1 传统的分布式运算(略)
- 7.2 使用偏移二进制编码的分布式运算(略)
- 7.3 分布式运算的ROM分解(略)
- 八. 结论
一. 引言
在DSP程序中,最为常见的运算就是乘法和加法。在高级设计中,常常会碰到乘法和加法的位级架构设计,涉及到位并行、位串行和数位串行三种实现类型。位并行系统每个时钟周期处理输入样点的一个字,占用资源多但速度快;位串行系统每个时钟周期处理输入样点的一个位,速度慢但占用资源少;而数位串行居于两者之间,是一个折中方案。
有符号数定点2的补码表示(2C):
一个W位[-1,1)的数A可表示为:
A = a 0 a 1 a 2 ⋅ ⋅ ⋅ a W − 1 = − a 0 + ∑ i = 1 W − 1 a i ⋅ 2 − i (1) A=a_0a_1a_2···a_{W-1}=-a_0+\sum^{W-1}_{i=1}a_i·2^{-i}\tag{1} A=a0a1a2⋅⋅⋅aW−1=−a0+i=1∑W−1ai⋅2−i(1)
其中, a 0 ∈ { 0 , 1 } ⋀ a i ∣ i = 1 , . . . , W − 1 ∈ { 0 , 1 } a_0\in\{ 0,1\}\bigwedge a_i|_{i=1,...,W-1}\in\{0,1\} a0∈{ 0,1}⋀ai∣i=1,...,W−1∈{ 0,1},根据2C数定义, a 0 a_0 a0称为符号位,公式(1)定义了一个 [ − 1 , 1 ) [-1,1) [−1,1)的小数。
对于公式(1)所表示的定点数记为S1.W-1。一般的,定点数SN.M,其中S表示一位符号位,N位整数位,M位小数位。
二. 并行乘法器
2.1 具有符号扩展的并行乘法
Horner法则:
多项式求值快速算法,可用于设计迭代乘法器,使用最少的乘法次数计算多项式的值,具体如下。
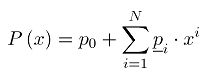
Horner法则将上式改写为下式:
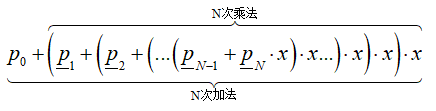
只需要N次乘法和N次加法。所需乘法次数Horner方式最少,乘法次数和加法次数恰好是多项式阶数大小。
例如具体的定点2的补码乘法如下:
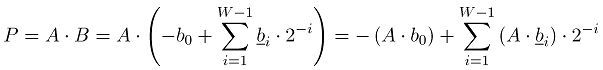
上式乘法运算变为取相反数或者右移( 2 − i 2^{-i} 2−i)操作。根据Horner法则设计的乘法公式如下:
![]()
并行乘法器(阵列乘法器)设计:

注意,第四行清楚的表示了补码的相反数即“当前补码每一位取反+LSB’1” 。上式写成竖式表格如下:

上图中上下两行相加,必须进行符号位对齐,即需要进行符号位扩展,如下图所示。
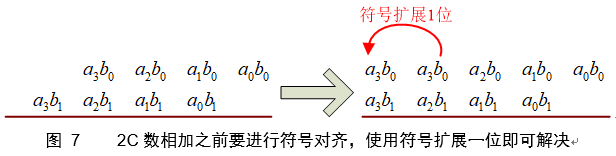
实际上如果不对输入进行限制,则最终计算结果可能内部溢出,解决方法是多进行一位符号扩展。若计算定长乘法,则方框中尾数可舍弃,如下图所示。
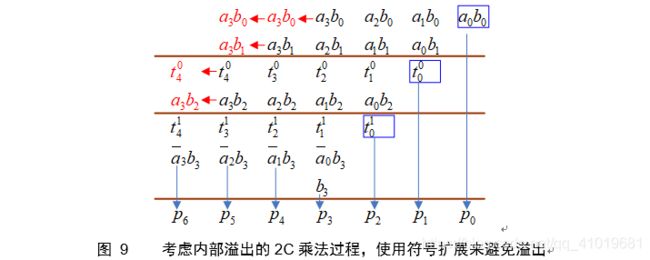
乘法器说本质就是多次部分积累加运算,快速完成多次累加的具体设计有下面串行进位和进位保留两种。
2.1.1 并行(串行进位)阵列乘法器
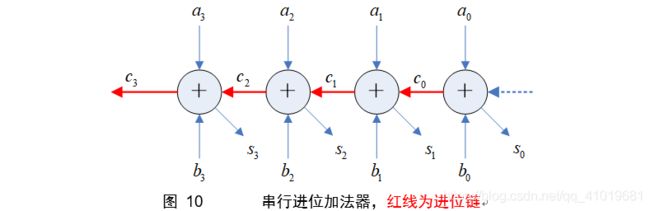
采用串行进位的阵列乘法器依赖图如下图所示,使用水平的割集流水线可将关键路径从2W(+1*)缩短为W。
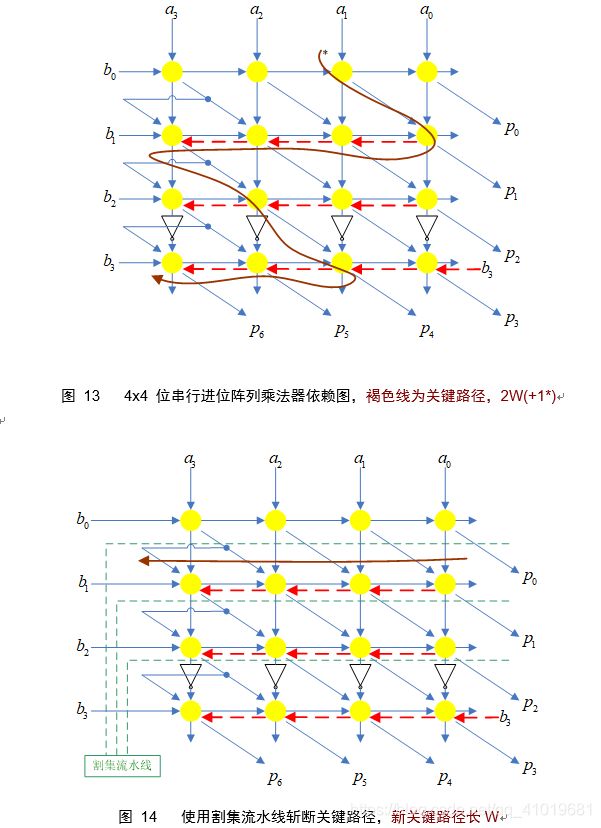
2.1.2 并行(进位保留)阵列乘法器
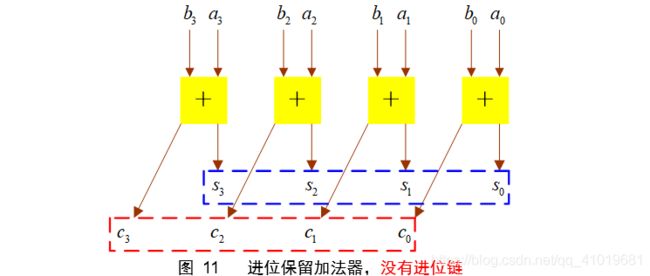
进位保留加法优势在于多次累加,将三个加数转化为二个加数。如下所示。
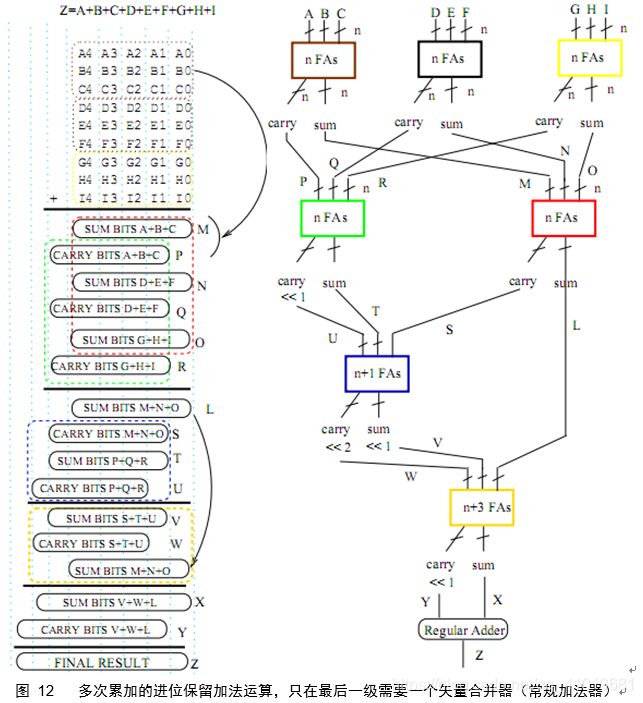
采用进位保留累加方式的阵列乘法器依赖图如下图所示,不计矢量合并器,关键路径长度为W-1(+1*),同样的可以使用割集流水线斩断关键路径,关键路径缩短为1。
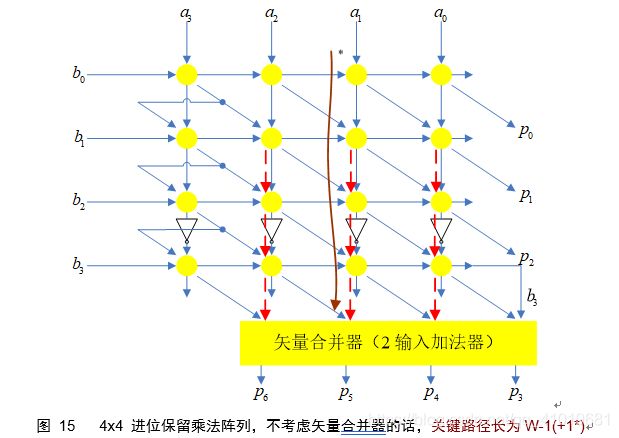
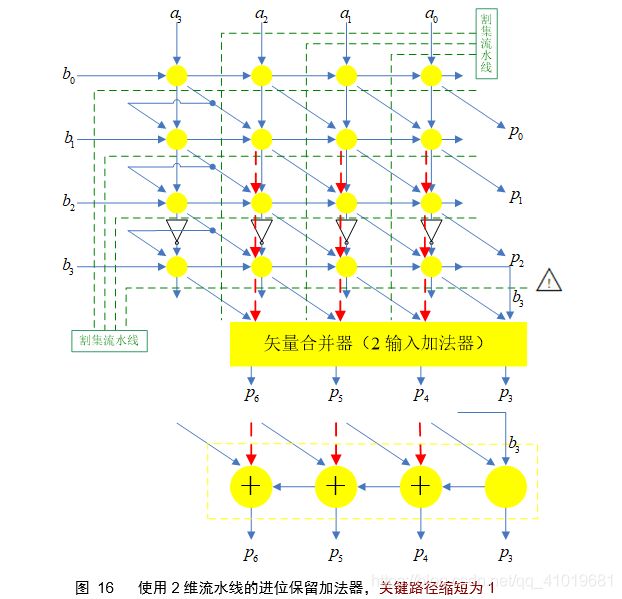
矢量合并加法器如下图所示。
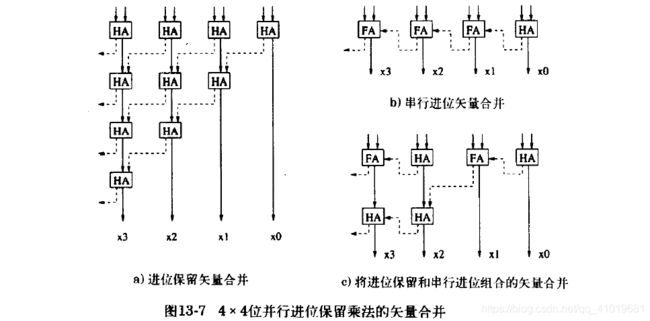
(注意)进位保留加法器符号扩展:除了第一次累加是正常符号扩展之外,第二次和第三次(除了矢量合并外所有后面的累加),其符号扩展应该是“和最高位 ⨁ \bigoplus ⨁相应的进位位”作为符号扩展,而不是“和最高位”作为符号扩展位!
2.2 Baugh-Wooley乘法器
将原始乘法公式变形:
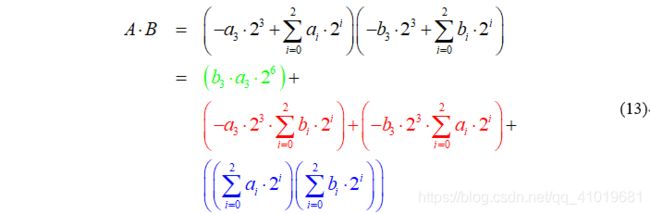
公式(13)红色部分两项都是纯粹的负数,首先将其转化为常规补码形式,如下:

然后可将公式(13)的三个部分组合在一起,如下图:
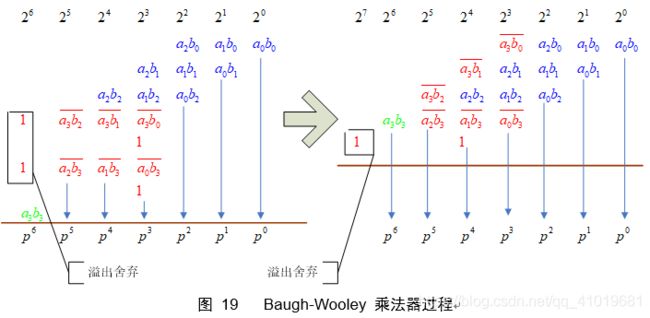
不用符号扩展就能实现乘法器,比一般2C乘法器要节省资源。
2.3 改进的Booth重编码并行乘法器
乘法运算设计两个部分,部分积的产生和部分积的累加。有两条提高乘法速度的途径:1)减少部分积的数目,2)加快部分积累加速度。进位保留加法器就是通过加快部分积累加速度来提高乘法器速度,如果只进行少量部分积累加的乘法器,可以通过改造数的编码,从而产生更少的部分积,典型的有Booth编码和CSD编码。
改进的Booth乘法器,对其中一个乘数进行重编码,如图 20,也就是说,将 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 → b 3 ′ b 2 ′ b 1 ′ b 0 ′ b_7b_6b_5b_4b_3b_2b_1b_0\rightarrow b'_3b'_2b'_1b'_0 b7b6b5b4b3b2b1b0→b3′b2′b1′b0′。
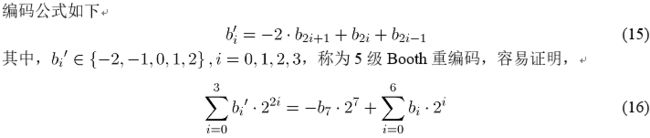
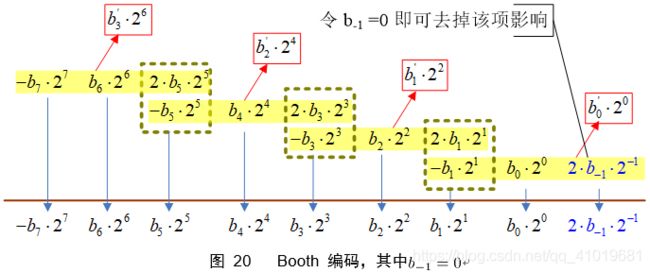
注意,改进Booth乘法只对其中一个乘数进行重编码,比如B,A仍然保持2C编码,所以
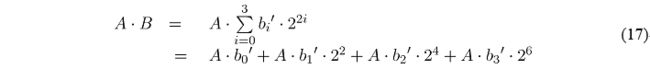
原本应进行7次部分积累加,现在最多只需进行3次部分积累加。
三. 交织布局规则与基于位平面的数字滤波器(略)
四. 位串行乘法器
4.1 利用Horner法则的Lyon位串行乘法器的设计
从无符号数的Horner位串行乘法器开始设计,之后再转入2C位串行乘法器设计,最后比较这两种设计的区别,弄清楚区别产生的原因所在。
无符号数乘法的Horner公式如下
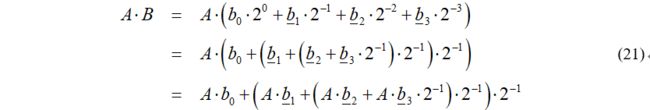
根据公式(21),画出一个系统框图如下(这不是位串行电路)
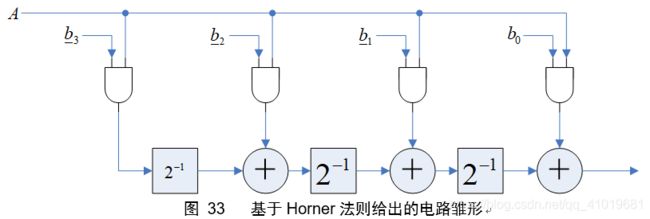
由图33的雏形电路设计出真正的位串行电路。
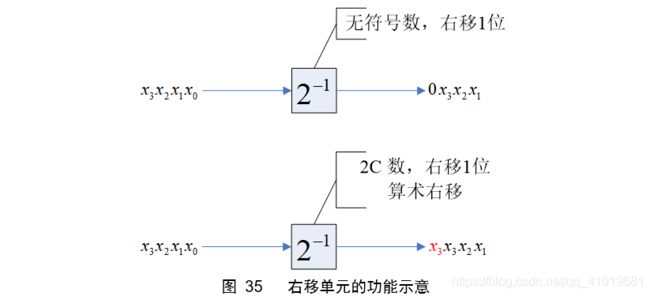
对于无符号数,右移之后最高位补零;对于2C数,右移之后最高位进行符号扩展。如果想用组合逻辑实现图35的功能,是做不到的,因为图35所示为非因果系统。
所谓的(无符号)左移单元其实就是一个延时器,从图 36可以看出,输入到输出被左移了一位,延时器的初始值应该为零。
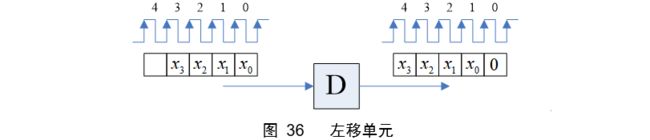
左移和右移的抵消,可以得到因果系统
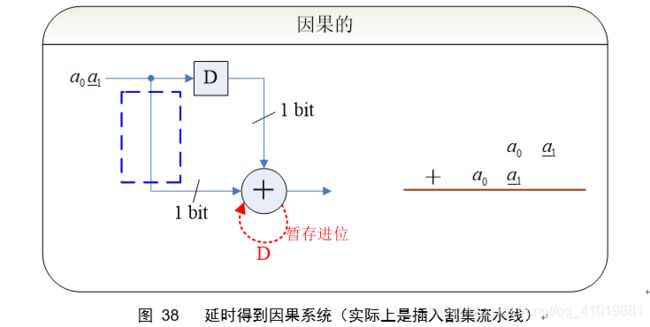
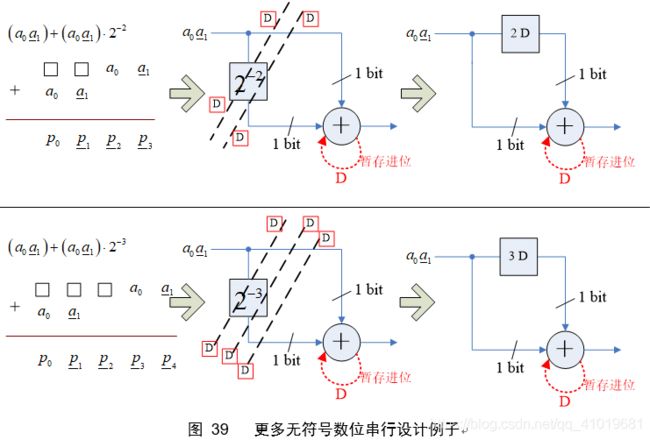
在无符号位串行的设计中,其实就是用一个延时单元(左移)来抵消右移一位( 2 − 1 2^{-1} 2−1),用两个延时单元抵消右移两位,三个延时抵消右移三位等等如此。
对于2C数的位串行设计仍然遵循“左移和右移的抵消”,但最终电路稍微变化,如下图
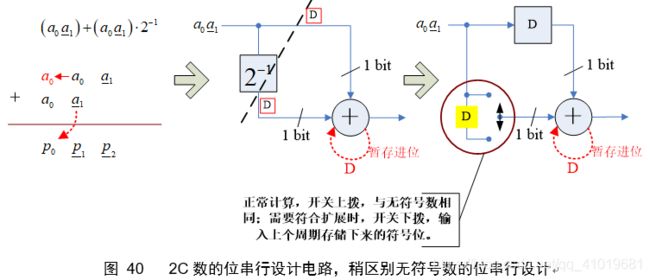
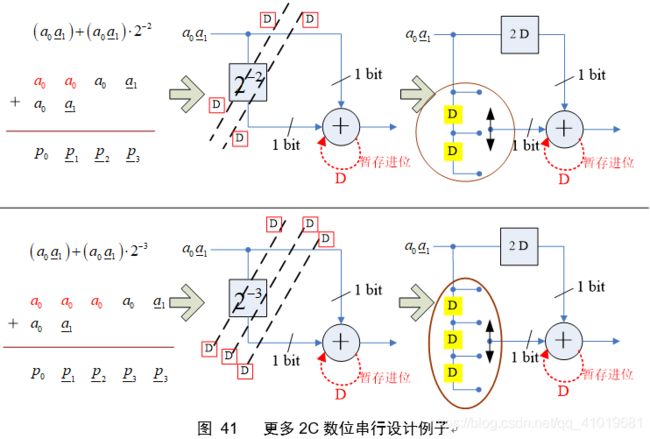
注意观察图41的电路,符号扩展功能其实可以设计得更为简洁,以便节约寄存器,所带来的坏处可能就是控制逻辑要复杂一些
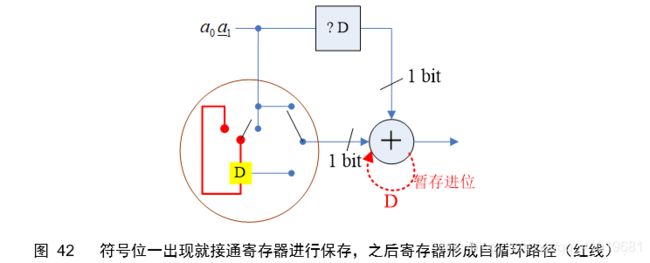
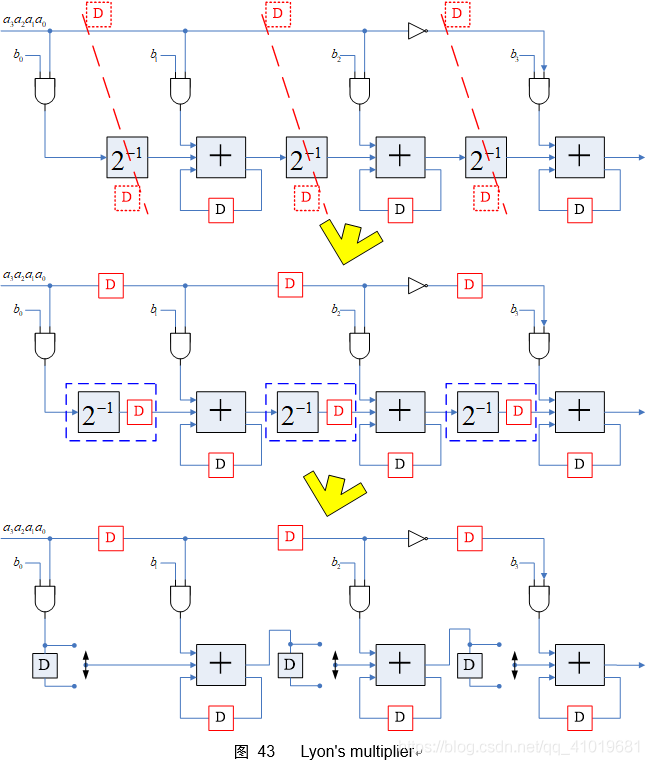
明白了以上的设计原则,设计Lyon乘法器就容易了,直接看图(4x4 Lyon’s multiplier)
4.2 利用脉动映射的位串行乘法器的设计
将标准并行乘法器经过脉动映射,就可以实现位串行乘法器,如下所示:
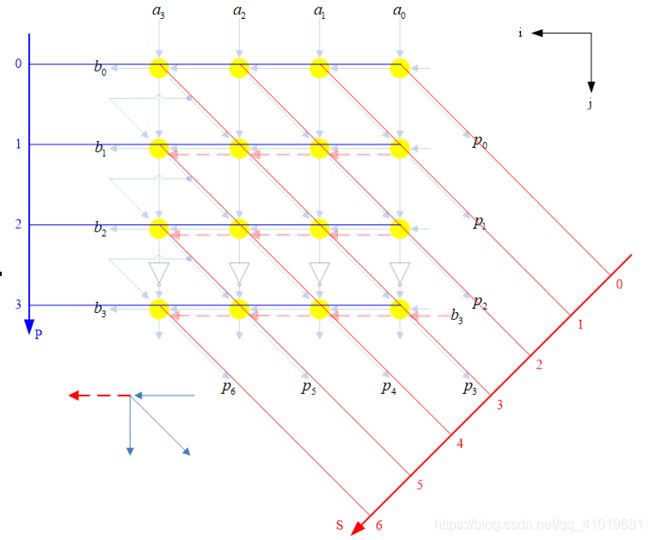
根据给出的时间轴和处理器轴,计算边映射关系如下,
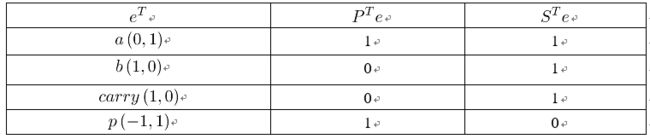
可画出脉动结构如
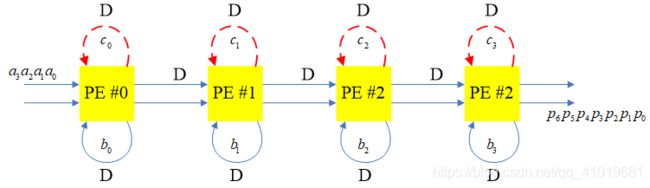
设计出具体的硬件电路
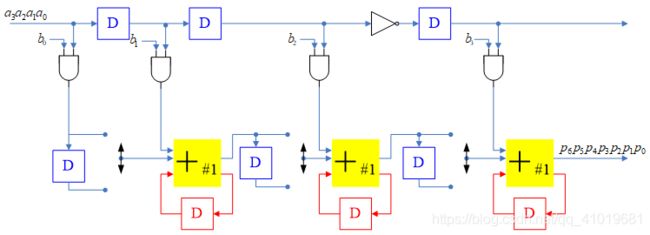
五. 位串行滤波器的设计与实现
5.1 位串行FIR滤波器
FIR位串行架构设计,假设FIR迭代公式如下
![]()
对于定点计算系统,总是能使用移位和加法来代替乘法,所以设计之前要先将迭代式的乘法转化为移位和加法,如公式(23)
![]()
字级电路如图 (44)
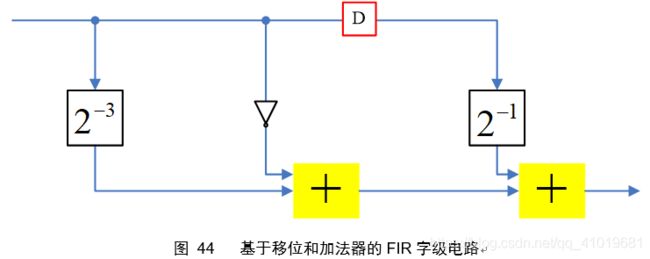
这里输入输出字长均为W=8。图44中的延时指的是字级的延时,转化到位级相当于W个延时,所以有
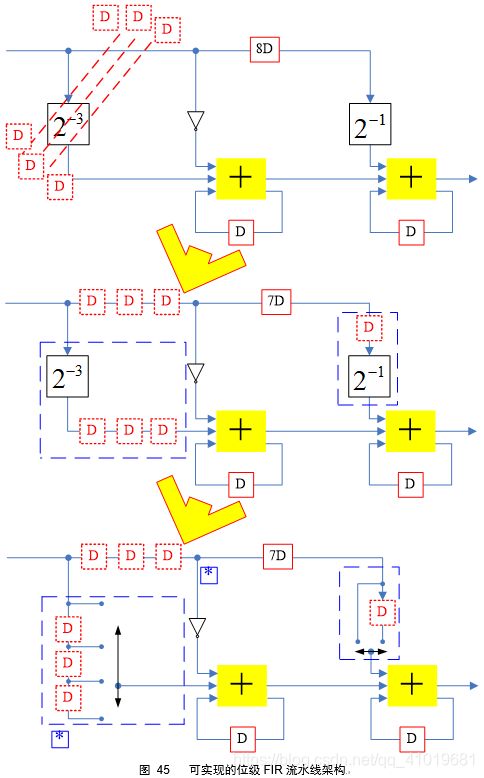
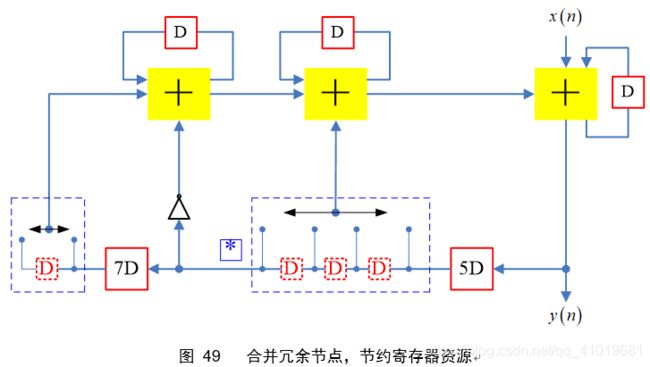
注意到图45最后电路的蓝色星号*,这两个节点可以合并,这样就能节约3个寄存器单元,最终电路如图 46
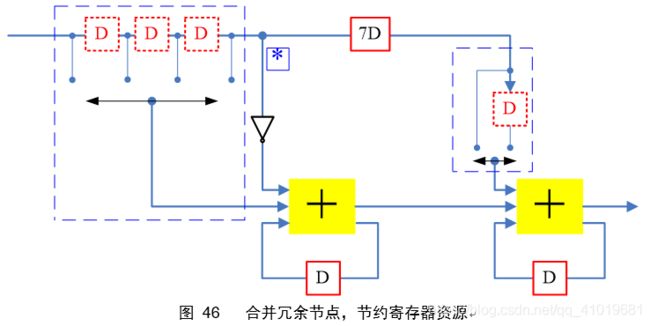
5.2 位串行IIR滤波器
(1)IIR位串行架构设计,假设IIR迭代公式如下
![]()
转化为移位和加法的实现,有
![]()
字级电路如下
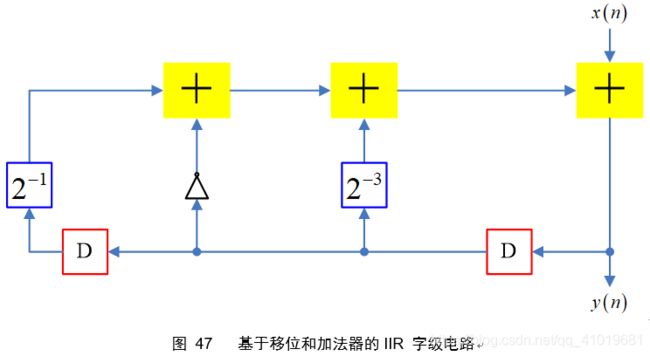
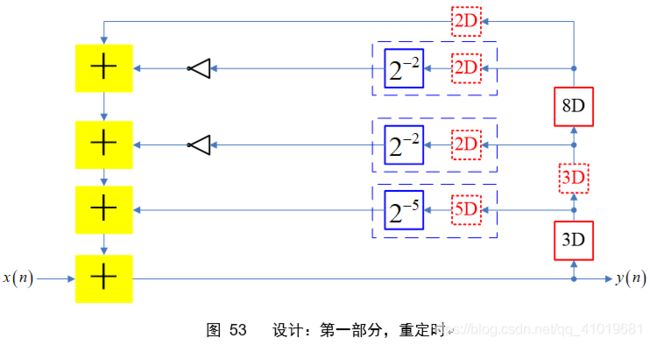
将图47转为位级架构,并用重定时移动恰当数目延时与右移单元相抵消,具体过程如图48
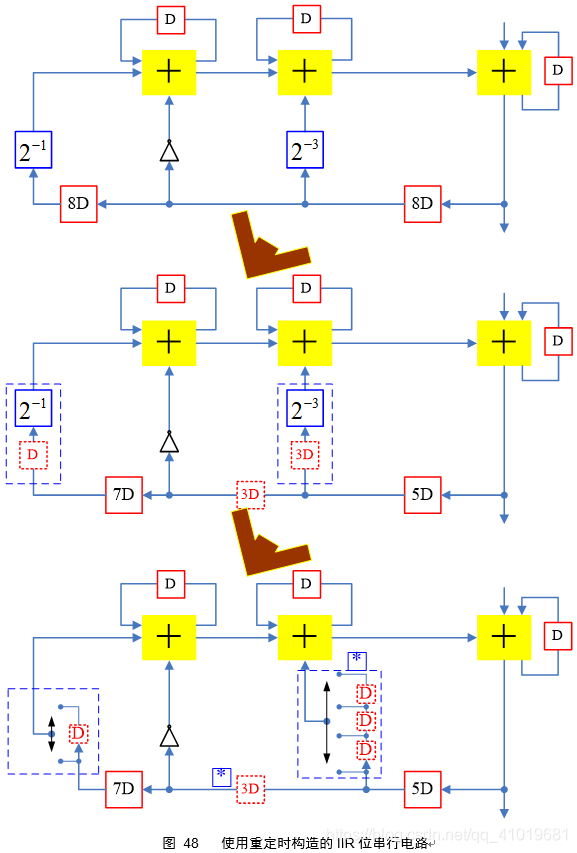
同样的,图48最后电路也可以进行节点共享,最终可得
(2)IIR位串行架构设计,假设IIR迭代公式如下
![]()
转化为移位和加法实现
![]()
![]()
请注意,图51的画图方法,两条准则:1)反相器位于右移单元之后;2)同一变量的不同右移支路,右移数目多的支路在前,右移数目少的支路在后。按照以上的准则画图,能容易观察出可以合并的节点,从而节约寄存器的使用。
先将图51字级电路转化为位级电路
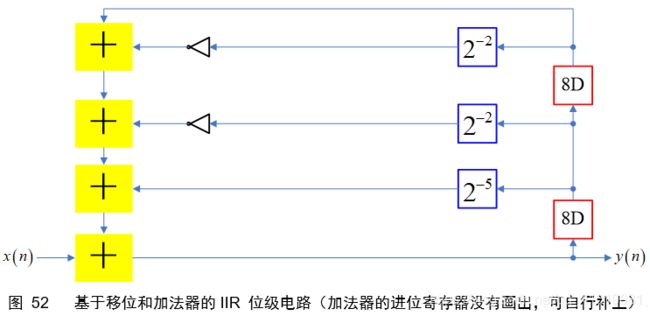
接下来对图52位级电路进行恰当重定时,并导出最终位级电路,如下图
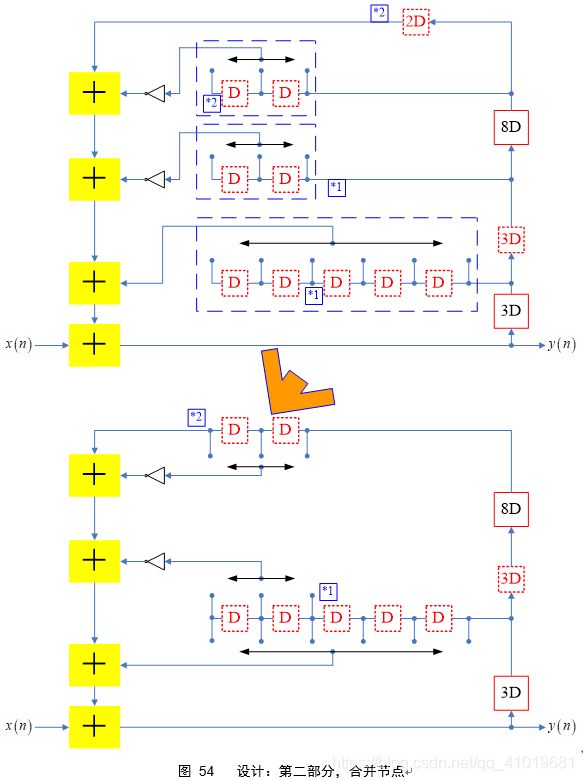
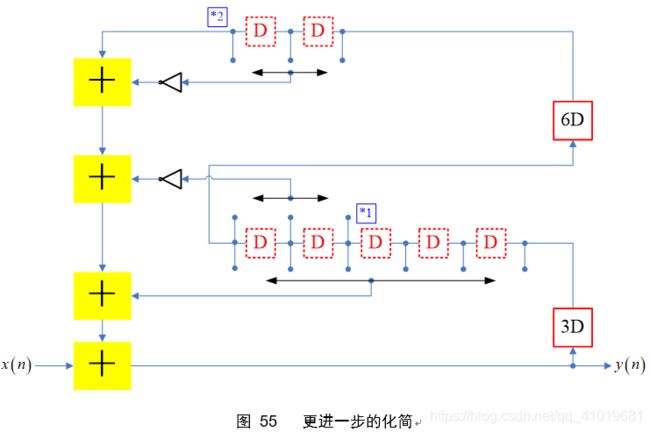
六. 正则符号数运算
一次常系数乘法所需的加法次数等于该常系数中非零位的数目减一。为了进一步减小面积和功耗,可以将常系数编码使得其中的非零位最少,这一点可以利用正则有符号数(canonic signed digit)(CSD)表示法实现。
6.1 CSD表示法
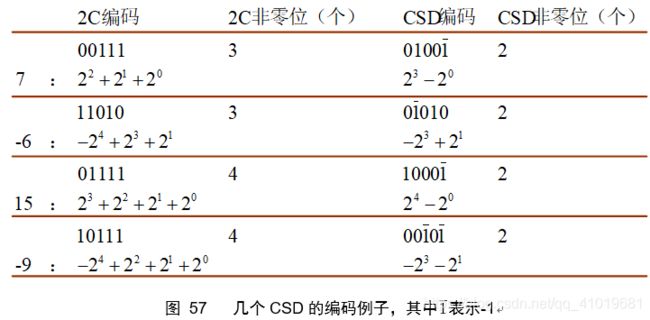
通过对比图 57同一个常数2C编码和CSD编码可知,CSD编码使用更少的非零比特位,另外一个区别是,CSD允许使用 位集合,而2C编码只能使用 位集合。其实CSD可以看作是二进制编码的一个扩展。
CSD编码扩展了 的取值集合,定义公式如下

一般情况下,我们只需知道如何将一个实数或者2C编码的串转化为CSD编码,就能用到实际中,可以不必太纠缠于CSD的一些理论讨论。

6.2 CSD乘法
得到常系数的CSD编码之后,就是具体的硬件实现过程。但实现过程中还有两个需要考虑的因素:累加的精度和累加的速度。举例说明,如 x × 0.10100 1 ‾ 0010 1 ‾ 00 1 ‾ x×0.10100\overline{1}0010\overline{1}00\overline{1} x×0.10100100101001
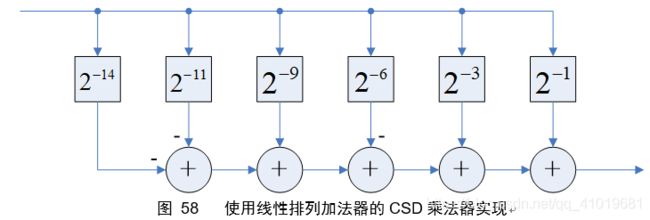
利用Horner法则可以提高计算精度,这里给出图形示意:
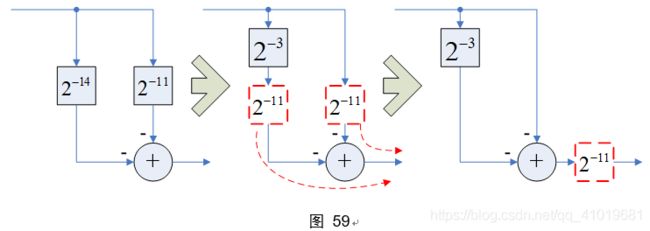
图59中可以将“一部分”移位单元移到加法器之后,下面的计算过程证明了这样做是对的
![]()
更进一步,为了加快CSD部分积累加的速度,应该采用二叉树加法排列,修改图58,得
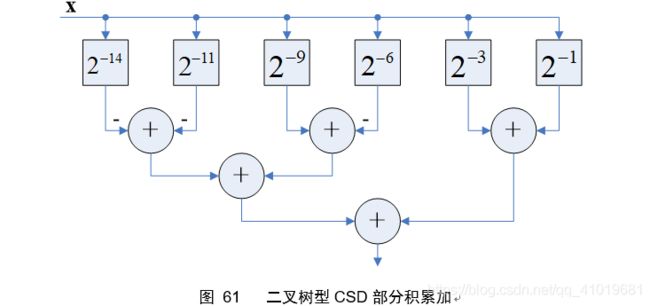
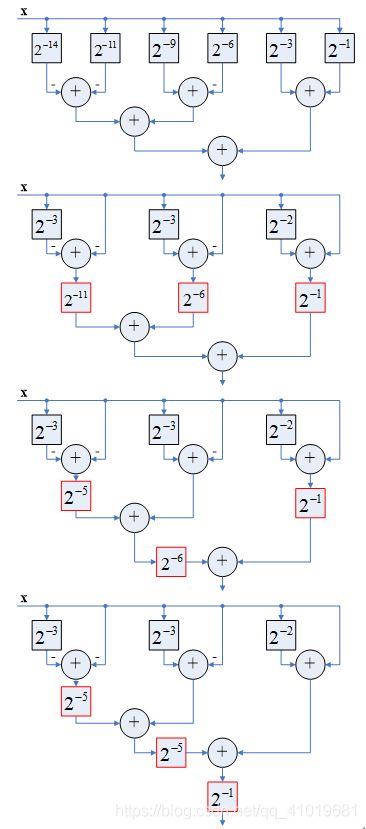
同样的,也可以将Horner法则应用到图61,如下图示时应用Horner法则和二叉树排列的CSD乘法器部分积累加电路
七. 分布式运算(略)
7.1 传统的分布式运算(略)
7.2 使用偏移二进制编码的分布式运算(略)
7.3 分布式运算的ROM分解(略)
八. 结论
本章讨论了位级运算架构的设计。介绍了位并行乘法器的设计,包括串行进位阵列、进位保留阵列、Baugh-Wooley和Booth重编码乘法。介绍了利用Horner法则和利用脉动映射的位串行乘法器的设计。本章还涉及了具有常系数的位级流水线位串行FIR和IIR滤波器的设计方法学。介绍了适用于低成本的高速常数系数乘法器的CSD表示法。
