使用matlab通过遗传算法实现多元函数极值计算

这里是对一个二元函数求解极大值问题。
如果你希望求解更多元函数，需要添加额外的基因（例如z）在pop数组中添加第三列（染色体的第三列基因），设置新的评判标准函数（fitness）。
如果你希望提高运算精度，可以尝试增大种群规模（优秀基因出现概率更高）、最大种群代数（更多次对优秀基因筛选）、提升变异概率（尝试引入新的可能更优秀的基因）。

个人对遗传算法的理解

遗传算法就是模仿自然规律，依照自然法则（评判标准函数，也就是你希望的目标），对一个初始种群（初始设置的一组解的集合）进行筛选，留下优秀的基因（相对较好的解）。通过种群内部的杂交（各种解的值随机互换）、基因变异（引入新的解，可能是优秀的解，也可能是坏的解），从而产生下一代种群，不断对种群通过自然法则（目标函数）的筛选，由于不断的杂交和变异会产生一些不同于之前的基因（解），因此在一定程度上可以保持种群的基因多样性（较多的比较合适的解）防止种群基因单一化（结果提前收敛），同时优秀的基因被保留（较优秀的解），因而种群基因总体向适应法则的方向发展（得出较为接近最优解的解）。

程序分析

程序初始化

我们需要设定种群规模，繁衍代数，变异几率。
你也可以设定一些其他的量，在二次修改的时候方便查找。

popsize=80;%设置种群规模
max_generation=1000;%初始化最大种群代数
Pmutation=0.2; % 变异概率

设置基因

基因个数=变量个数
这些基因就是你的自然法则判断该物种是否适应的标准（解是否符合目标期望）
这里考虑二元变量，所以两个基因就是x和y。因为rand函数默认生成0到1之间的随机数，如果想把x（y）放置到指定的集合，就可以用这样的表达：
rand函数用于产生k，△就是区间长度也就是max-min

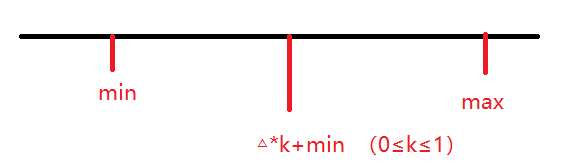
下面的代码中x和y是基因，pop是由x和y组成的染色体（n多组解的集合）；
x_lable是我之前进行debug时保留的（入过你刚好也需要检查修改时就可以用，其他时候请忽略或删除）
xn和yn用于生成后面的一个临时数组popex（仅做一个占位作用，之后会删除掉该组值），这个数组的值理论上可以是任意值，但为了防止引入一些不合适的值，这里选择随机一组解

x=x_min+(x_max - x_min)*rand(popsize,1);
y=y_min+(y_max - y_min)*rand(popsize,1);
pop=cat(2,x,y);%**************************
x_lable=[1:max_generation];
xn=x_min+(x_max - x_min)*rand(1,1);
yn=y_min+(y_max - y_min)*rand(1,1);
pop_ex=[xn yn];

演化进程开始

这是一个大的循环，循环次数由前面的max_generation确定。
通过适应度函数对所有解进行适应度考核，将考核数据保存到fitness中，选取其中的最大值（此为这一代中最优的个体基因，必须要保留）。使用best_pop数组保存这一个优秀解。
那前面的mv_id=mv_id1(1,1)是什么作用呢？
在演算过程中，难免出现种群中有多个最优秀个体（解参数相同），这时取max时就会取到多个列参数，best_pop在一次循环中就会保存多个相同解。
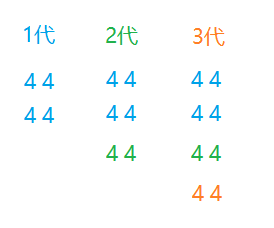
下图演示了这种过程，如果一代存在两个优秀解，由于有保留优秀的的机制，两个相同的解会直接添加到二代的种群中，由于种群数目庞大，难免在下一次循环中出现相同的解，也难免下一代中能产生比一代优秀解更好的解。这样几次循环就会在种群中出现同一基因（解）的大量个体。为了提高运算速度，我们不可能无限将种群规模扩大，只能将种群规模设置一个上限（因为有循环次数加持，如果每一代种群规模都在增长，几代就可以使种群规模暴涨）。然而限制了种群规模，你也可以看到当下面这种44（优秀组合）增加的时候可能会快速充满种群，使多样性降低，导致提前收敛而降低算法精度
因此在找出优秀解后限定每一回合只保留它（它们）中的一个，就可以防止这种优秀基因填满种群的状况

for generation = 1:max_generation 
    fitness=x.^2+y.^2;
    mv=max(fitness);
    [mv_id1,nv]=find(fitness==mv);%找到这一代中最优解
    mv_id=mv_id1(1,1);
    best_pop=pop(mv_id,:);%保存这一代最好的数据

选择

有优秀个体直接参加下一循环，自然要对其他个体也进行排序，淘汰掉一些较差个体或保留一些相对较好的个体。
设置两个随机排序i01,i02，这是行向量，所以需要转成列向量再进行比较。
下图展示了一个例子，这里最终淘汰了4、6、7号，虽然7号个体也比较优秀（但生不逢时，遇到了1）。

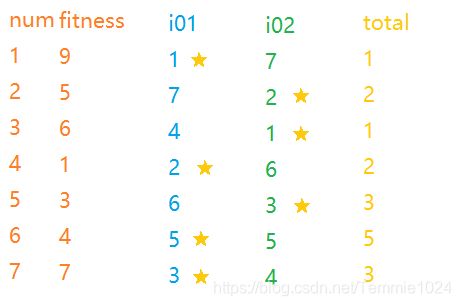
可以看到我下面的代码中生成i01和i02使用了randperm函数，使用rand再转化成整数的方法可以吗？
答：最好不要这样用。rand随机出的数通过向某一方向取整，经常出现取整后多个值是相等的（即取出11122345555）列，在两列都是这种数的情况下，大多数比较的结果得出的都是重复的数（多次保留了同一个个体，导致种群基因多样性急剧下降）。相比rand，randperm随机产生的数无法重复，这就限制了两两比较最多只能出现的重复不超过两个，种群多样性保持会更好。

	 i01 =randperm(popsize);
     i02 =randperm(popsize);
     i1=transpose(i01);
     i2=transpose(i02);
     I = i1.*( fitness(i1)>=fitness(i2) )+i2.*( fitness(i1)< fitness(i2) );
     pop0=pop(I,:);%**************************************************

交叉

对多有个体的基因（解）进行交换。从第一个个体开始，两两一组，对x或y进行交换（只需交换一个，如果两个都交换就等于没交换了，不信自己画一画就知道了）
由于这里是两两一组，因此如果种群个体存在奇数，最后一个就无法找到个体交叉（单身狗，汪汪汪！）不过一个个体影响也并不大，可以略去。
由于每次交换是一个1*2的数组，最终还是要拼成之前的染色体（解集合），因此在这里使用pop_ex进行拼接，每次在pop_ex下方拼接两组解，直到循环结束。
为了和这些解的数组格式一致，在拼接之前，我在pop_ex中人为添加了一组解，拼接过程借宿后需要删掉（不然每一次大循环都将导致种群个体数+1，在循环次数大的情况下这一点也不好玩。）由于是向下拼接，所以我添加的解就在第一行，原解集合就是第二行到倒数第二行，这里实际有种群个体数-1个个体，因为等这次循环结束后，还要添加该回合最优解，需要提前留出位置。（倒数第一突然暴毙）

for i = 2:2:popsize
    parent1 = pop(i,:);  child1 = parent1;
    parent2 = pop(i-1,:);  child2 = parent2;
    child1(1,2)=parent2(1,2);
    child2(1,2)=parent1(1,2);
    pop_ex=[pop_ex;child1;child2];%******************************************
    end
    lin=[2:popsize];
    pop=pop_ex(lin,:);

变异

按照一定概率对种群中个体的解进行改变，概率大小取决于之前设定的变异概率。人为引入新的解因子。

 for k=1:popsize-1
        if rand<=Pmutation
            pop(k,1)=x_min+(x_max - x_min)*rand;
            pop(k,2)=y_min+(y_max - y_min)*rand;
        end
    end

循环结束

这一轮循环结束，由于保留优秀基因的原则，在对种群选择、交叉、变异之后添加之前的最优解组。接下来就是一些检验了，如在你知道函数最大值位置时绘制最优解位置，了解它们之间的接近程度。
另外，最重要的是为下一次循环做准备x=pop(:,1); y=pop(:,2);两句就是在设置下一循环开始时解集合的初始值（第一次的初始值在大循环之外，使用一次之后就无效了。一定要注意这一点，我debug了好几次才发现这个致命的问题）

%这一代结束后，种群构成
    pop=[best_pop;pop];%**************************************************
    x=pop(:,1);
    y=pop(:,2);
    %绘制该点
    px=best_pop(1,1);
    py=best_pop(1,2);
    plot(px,py,'*');%*************************************************
    hold on;

输出

输出就很随意了，想输出什么直接赋给它就可以了。
另外，代码中后面出现%*****************的是我个人debug时的一些关键位置，打上断点，将这一行的分号去掉，运行时观察数组集合的值、大小的变化。

%输出最优结果
endpop=pop;
max_value = max(fitness(mv_id));
max_pop =best_pop
end

完整代码

还有许多地方需要优化，自己第一次写，能力有限，还请见谅

function [max_value] = Binary_function_operation(x_min,x_max,y_min,y_max)
%摘要     Binary_function_operation(0,4,0,4)
%输入函数f，x的取值范围，y的取值范围
%f函数 x_min第一个变量的最小取值 x_max第一个变量的最大取值 y_min第二个变量的最小取值 y_max第二个变量的最大取值

%一些初始数据设置，如果对精度不满意可以修改
popsize=80;%设置种群规模
max_generation=1000;%初始化最大种群代数
Pmutation=0.2; % 变异概率

%初始化种群，随机产生popsize组解
x=x_min+(x_max - x_min)*rand(popsize,1);
y=y_min+(y_max - y_min)*rand(popsize,1);
pop=cat(2,x,y);%**************************
x_lable=[1:max_generation];
xn=x_min+(x_max - x_min)*rand(1,1);
yn=y_min+(y_max - y_min)*rand(1,1);
pop_ex=[xn yn];

%主循环
for generation = 1:max_generation 
    fitness=x.^2+y.^2;
    mv=max(fitness);
    [mv_id1,nv]=find(fitness==mv);%找到这一代中最优解
    mv_id=mv_id1(1,1);
    best_pop=pop(mv_id,:);%保存这一代最好的数据
    %选择（竞争模式）
     i01 =randperm(popsize);
     i02 =randperm(popsize);
     i1=transpose(i01);
     i2=transpose(i02);
     I = i1.*( fitness(i1)>=fitness(i2) )+i2.*( fitness(i1)< fitness(i2) );
     pop0=pop(I,:);%**************************************************
    %交叉
    for i = 2:2:popsize
    parent1 = pop(i,:);  child1 = parent1;
    parent2 = pop(i-1,:);  child2 = parent2;
    child1(1,2)=parent2(1,2);
    child2(1,2)=parent1(1,2);
    pop_ex=[pop_ex;child1;child2];%******************************************
    end
    lin=[2:popsize];
    pop=pop_ex(lin,:);
    %变异
    for k=1:popsize-1
        if rand<=Pmutation
            pop(k,1)=x_min+(x_max - x_min)*rand;
            pop(k,2)=y_min+(y_max - y_min)*rand;
        end
    end
    %这一代结束后，种群构成
    pop=[best_pop;pop];%**************************************************
    x=pop(:,1);
    y=pop(:,2);
    %绘制该点
    px=best_pop(1,1);
    py=best_pop(1,2);
    plot(px,py,'*');%*************************************************
    hold on;
end

%输出最优结果
endpop=pop;
max_value = max(fitness(mv_id));
max_pop =best_pop
end