源码分享：C++矩阵类CLMatrixT，功能强大使用简单，支持内存池、宽指令、并行化加速！持续更新...

C++矩阵类模板CLMatrixT介绍：

最近在研究AI和深度学习，矩阵计算代码基本全是python的，C++基本没有成熟的库。而矩阵计算中，许多python的矩阵计算例子用法都很简单，感觉C++也应该有属于自己的矩阵处理类，即可享受C++的速度又可享受面向对象编程方便。但是网上找了很多已有的代码都很单一，作为C++的执着，收集一些资料后重写了这个类模板（再次感谢网上提供过相关C++源码的小伙伴，你们的工作给了我很多基础）。
本着人人为我我为人人的精神，现在分享源码给大家，希望大家多指点！源码暂时是windows下vc写的，所以有其他需求的小伙伴，可自行修改、补充、或移植到其他平台；

特点

1. 面向对象，保证使用时代码简洁；
2. 可以方便的做：四则混合运算、取指数、取幂、开根、自定义等等运算操作；
3. 构造、赋值、修改的方案，可由用户通过lambda表达式自定义；（要求支持c++14）

新增功能

1. 增加内存池支持，大大提速四则混合运算速度；【C++内存池实现源码】【该功能可关闭】
2. 增加SSE/AVX浮点运算支持，加速计算，高阶矩阵运算提速更明显；【该功能可关闭】
3. 增加多种点乘算法；
4. 增加卷积运算；
5. 增加矩阵乘法、卷积运算的宽指令及并行化加速；(乘法，点乘、卷积运算速度高于Numpy)

先演示使用方法：

高级用法，详见：【源码分享：C++矩阵类，快速搭建神经网络，实现sin和cos函数逼近源码】

以下演示对象的：
创建、自定义赋值、行列式、奇异性判断、求逆、四则运算、LU分解、卷积、输出等操作。
本类还有很多其他的功能均已实现，使用者自行查看类源码，自己发掘使用方法，在此不一一演示。
可以和Matlab或者numpy做个比较，看看是否更实用！！

//designed by cailuo @2020-02-10 
//mini-support @ c++14
#include "CLMatrix.h"
//...
//注意：头文件请在代码中自行引用，以下只给出测试的主要代码。
//...
int main() {
     

	srand(time(0));
	//带lambda表达式自定义赋值方案的构造函数，生成8阶方阵,每项设为一个随机值
	CLMatrix M(8, 8, [](double& i, size_t r, size_t c) {
      i = (rand() % 1000) * 0.01; });
	//验证矩阵求逆并相乘得到单位矩阵E，并逐个输出矩阵内容
	(M.print("原矩阵M") * M.inv().print("逆矩阵_M")).print("验证 M * _M = E ");
	printf("\n\n矩阵 M ： %s奇异矩阵，行列式值= %g \n\n", M.isSingularMatrix() ? "是" : "不是", M.det());

	//由make方法构造矩阵，并按自定义方式赋值各项
	CLMatrixT<double> A1, A2;//元素为double类型的矩阵
	CLMatrixT<float>  D1, D2;//元素为float类型的矩阵，类型不同并不会影响计算
	A1.make(5, 7, [](double& i, size_t r, size_t c) {
      i = (rand() % 1000) * 0.01; });
	A2.make(7, 5, [](double& i, size_t r, size_t c) {
      i = (rand() % 1000) * 0.01; });
	D1.make(5, 5, [](float& i, size_t r, size_t c) {
      i = (rand() % 1000) * 0.01; });
	//此处通过拷贝操作，更改D1矩阵（5行5列方陈）5行0列至3行3列范围的值来生成新的D2矩阵
	D2 = D1.operate([](float& i, size_t r, size_t c) {
      i = (rand() % 1000) * 0.01; },5,0,3,3);

	//下列演示矩阵的四则混合运算：加、减、承、除、自加、自减、取指数、幂计算。
	//其中operate操作实现了自定义的幂操作（可用内部已实现的exp()函数替代）；
	//operate()和reset()等操作允许自定义对矩阵元素做处理
	auto R = (0.55 * A1 * A2 * 0.5 + 0.4 * D1 / D2 - D1 + ++D2--)
				.pow(1.25).operate([](double& i, size_t r, size_t c) {
      i = exp(i);});
	R.print("四则混合运算结果矩阵R");

	//演示矩阵 M 的 LU 分解
	CLMatrix L, U;
	M.LU(L, U);
	L.print("L");//输出矩阵
	U.print("U");
	(L * U).print("LU");//验证计算结果
	
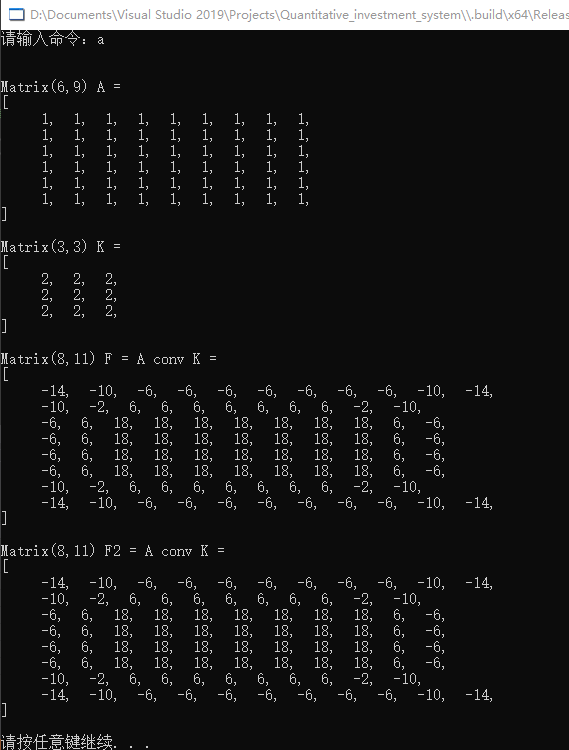
	//演示 A conv K 卷积运算
	CLMatrixF A = {
       //输入map = { 6 X 9 }
		{
     1,1,1,1,1,1,1,1,1 },
		{
     1,1,1,1,1,1,1,1,1 },
		{
     1,1,1,1,1,1,1,1,1 },
		{
     1,1,1,1,1,1,1,1,1 },
		{
     1,1,1,1,1,1,1,1,1 },
		{
     1,1,1,1,1,1,1,1,1 },
	};
	CLMatrixI K = {
       //卷积核kernel = { 3 X 3 }
		{
     2,2,2,},
		{
     2,2,2,},
		{
     2,2,2,},
	};
	CLMatrix F;
	conv(A, K, F,1,1,2,-1.0); //全局函数调用，X、Y方向移动步长=1，padding = 2，paddingValue = -1.0
	auto F2 = A.conv(K, 1,1,2,-1);//对象调用卷积，X、Y方向移动步长=1，padding = 2，paddingValue = -1.0

	A.print("A");
	K.print("K");
	F.print("F = A conv K");
	F2.print("F2 = A conv K");
	
	getchar();
	return 1;
}

再看运行测试结果：

矩阵求逆演示：------------------------------------------------------------------------------------------------
Matrix(8,8) 原矩阵M =
[
1.66, 3.82, 2.65, 0.19, 5.11, 0.42, 3.91, 4.81,
1.22, 2.81, 1.75, 9.36, 8.19, 1.02, 4.75, 0.23,
3.5, 5.59, 6.78, 9.72, 3.17, 3.47, 7.51, 6.96,
3.24, 6.53, 0.58, 7.37, 7.37, 0.64, 6.87, 9.36,
0.39, 6.76, 1.99, 8.13, 5.25, 3.36, 3.16, 5.19,
7.15, 0.24, 3.92, 6.72, 5.49, 7.69, 8.01, 0.73,
7.31, 6.18, 2.19, 6.98, 7.43, 4.78, 1.11, 3.64,
9.84, 0.07, 0.83, 5.94, 2.39, 4.69, 8.65, 7.73,
]
Matrix(8,8) 逆矩阵_M =
[
-0.263753, -0.164733, 0.108588, 0.391525, -0.399647, 0.167746, 0.159207, -0.225317,
-0.760534, -0.616338, 0.234001, 1.25243, -0.751357, 0.664719, 0.183165, -0.880194,
0.388377, 0.236578, 0.05688, -0.566098, 0.207112, -0.281586, -0.019738, 0.282378,
-0.000986692, 0.156835, 0.0124086, -0.194232, 0.126657, -0.152925, -0.0110498, 0.15457,
0.45004, 0.322463, -0.177309, -0.566359, 0.357562, -0.288902, -0.0500384, 0.366574,
0.181743, 0.0224353, -0.144535, -0.333249, 0.39651, -0.034011, -0.0742567, 0.191859,
-0.466269, -0.356774, 0.13288, 0.83965, -0.510227, 0.49941, -0.0121912, -0.534446,
0.57404, 0.355284, -0.16217, -0.861981, 0.615801, -0.520696, -0.119547, 0.64337,
]
Matrix(8,8) 验证 M * _M = E =
[
1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 0, 0, 1,
]
矩阵 M ： 不是奇异矩阵，行列式值= 797684

四则混合运算演示：------------------------------------------------------------------------------------------------
Matrix(5,5) 四则混合运算结果矩阵R =
[
8.28536e+41, 1.59025e+50, 4.18218e+91, 1.0208e+88, 9.0689e+90,
4.54326e+15, 1.88274e+39, 1.26615e+27, 5.03404e+42, 2.45859e+42,
3.47545e+18, 4.14339e+33, 3.4207e+39, 1.0388e+51, 8.8166e+46,
1.76522e+21, 4.44433e+25, 5.00863e+69, 3.17953e+51, 3.61687e+64,
5.92095e+35, 2.99281e+34, 3.20721e+72, 3.83364e+73, 1.09172e+64,
]

LU分解演示：------------------------------------------------------------------------------------------------
Matrix(8,8) L =
[
1, 0, 0, 0, 0, 0, 0, 0,
0.0396341, 1, 0, 0, 0, 0, 0, 0,
0.355691, 0.823578, 1, 0, 0, 0, 0, 0,
0.168699, 0.563573, 0.288739, 1, 0, 0, 0, 0,
0.123984, 0.414567, 0.171507, -0.924864, 1, 0, 0, 0,
0.726626, 0.0279902, 0.669435, -0.258561, 0.666236, 1, 0, 0,
0.742886, 0.906881, -0.0413415, 0.814721, -0.123507, -0.0606041, 1, 0,
0.329268, 0.962962, -0.32381, 0.327948, 0.0268482, -0.595664, -0.138688, 1,
]

Matrix(8,8) U =
[
9.84, 0.07, 0.83, 5.94, 2.39, 4.69, 8.65, 7.73,
0, 6.75723, 1.9571, 7.89457, 5.15527, 3.17412, 2.81716, 4.88363,
0, 0, 4.87295, 1.1054, -1.92587, -0.812323, 2.11312, 0.18846,
0, 0, 0, -5.58041, 2.35751, -1.9255, 0.252935, 0.699258,
0, 0, 0, 0, 8.26715, -2.51887, 2.38115, -2.13859,
0, 0, 0, 0, 0, 5.91738, -1.28977, -3.54407,
0, 0, 0, 0, 0, 0, -7.77359, -7.5722,
0, 0, 0, 0, 0, 0, 0, -1.16012,
]

Matrix(8,8) LU =
[
9.84, 0.07, 0.83, 5.94, 2.39, 4.69, 8.65, 7.73,
0.39, 6.76, 1.99, 8.13, 5.25, 3.36, 3.16, 5.19,
3.5, 5.59, 6.78, 9.72, 3.17, 3.47, 7.51, 6.96,
1.66, 3.82, 2.65, 0.19, 5.11, 0.42, 3.91, 4.81,
1.22, 2.81, 1.75, 9.36, 8.19, 1.02, 4.75, 0.23,
7.15, 0.24, 3.92, 6.72, 5.49, 7.69, 8.01, 0.73,
7.31, 6.18, 2.19, 6.98, 7.43, 4.78, 1.11, 3.64,
3.24, 6.53, 0.58, 7.37, 7.37, 0.64, 6.87, 9.36,
]

卷积计算结果：

最后分享源代码：

头文件需要用到的内存池支持"CLMemPool.h"源码，不包含该文件则不启用内存池支持。

源文件：CLMatrix.cpp

#include "CLMatrix.h"
unsigned long long matrixCreateTimes = 0;//统计计数
bool matrixUseSSE = true;                //使用SSE/AVX指令
size_t matrixUseSSEMinRank = 10;         //使用SSE/AVX指令的最低矩阵宽度

头文件名：CLMatrix.h

//DESIGNED BY CAILUO @2020-02-10 
//MINI-SUPPORT @ C++14

#pragma once
#ifndef __CL_MATRIX_H__
#define __CL_MATRIX_H__

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include  //其他平台注释掉

using std::vector;
using std::string;
using std::wstring;
using std::cout;
using std::cin;
using std::istream;
using std::ostream;

#include   //用于设置输出格式

using std::ifstream;
using std::ofstream;
using std::istringstream;
using std::cerr;
using std::endl;

#define CLMAT_USE_SSE      1 //当为1时使用SSE/AVX指令加速
#define CLMAT_USE_MEMPOOLS 1 //当为1时使用内存池技术加速

#if CLMAT_USE_MEMPOOLS > 0
#include "CLMemPool.h"
#else
extern unsigned long long matrixCreateTimes;
#endif

//当设置该变量为true时候启动SSE,AVX指令加速。
//该变量需要在cpp定义为全局变量，并设置该全局量。
extern bool matrixUseSSE;

//使用SSE,AVX指令的最低矩阵宽度，他的大小影响本机矩阵运算效率；
//一般为根据本机计算性能决定（8-16间），可使用matrixSSEParamFitValue()获得本机该值的最佳值；
//该变量需要在cpp定义为全局变量，并设置该全局量为一个初始值；
extern size_t matrixUseSSEMinRank;

#ifndef _CL_DIFVARS_SUPPORT_
#define _CL_DIFVARS_SUPPORT_
#ifdef UNICODE
typedef wchar_t Char;
#define tstring wstring
#ifndef _T
#define _T(x)  L ## x
#endif
#ifndef _tprintf_s
#define _tprintf_s wprintf_s
#define _stprintf_s swprintf_s
#define _tcscpy_s wcscpy_s
#endif
#else
typedef char Char;
#define tstring string
#ifndef _T
#define _T(x)  x
#endif
#ifndef _tprintf_s
#define _tprintf_s printf_s
#define _stprintf_s sprintf_s
#define _tcscpy_s strcpy_s
#endif
#endif
typedef const Char* PCStr;
typedef Char* PStr;
#ifndef BUFSIZE
#define BUFSIZE 256
#endif
#ifndef max
#define max(a,b) ((a) < (b) ? (b) : (a))
#define min(a,b) ((a) < (b) ? (a) : (b))
#endif
#endif

template <class T1> T1 LxAbs(T1 d)
{
     
	return (d >= 0) ? (d) : (-d);
}
template<class T1> bool isSignRev(const std::vector<T1>& v)
{
     
	size_t p = 0;
	size_t sum = 0;
	size_t n = (size_t)v.size();

	for (size_t i = 0; i < n; ++i)
	{
     
		p = (size_t)v[i];
		if (p >= 0)
		{
     
			sum += p + i;
		}
	}

	if (sum % 2 == 0) // 如果是偶数，说明不变号
	{
     
		return false;
	}
	return true;
}
template <class T1>class CLMatrixT;
template<class T1> size_t max_idx(const CLMatrixT<T1>& m, size_t k, size_t n)
{
     
	size_t p = k;
	for (size_t i = k + 1; i < n; ++i)
	{
     
		if (LxAbs(m[p][k]) < LxAbs(m[i][k]))
		{
     
			p = i;
		}
	}
	return p;
}
//sse指令集数据拷贝
template<class Ty> void memcpy_sse(Ty* left, const Ty* right, size_t nCounts) {
     
	struct block_4 {
      Ty a[4]; };
	struct block_8 {
      Ty a[8]; };
	struct block_16 {
      Ty a[16]; };
	if (nCounts < 4) {
     
		for (size_t j = 0; j < nCounts; ++j)
			left[j] = right[j];
	}
	else if (nCounts < 16) {
     
		size_t sj = nCounts / 4 * 4;
		for (size_t j = 0; j < sj; j += 4)
			*(block_4*)&left[j] = *(block_4*)&right[j];
		for (size_t j = sj; j < nCounts; ++j)
			left[j] = right[j];
	}
	else {
     
		size_t sj = nCounts / 16 * 16;
		size_t sj2 = nCounts / 4 * 4;
		for (size_t j = 0; j < sj; j += 16)
			*(block_16*)&left[j] = *(block_16*)&right[j];
		for (size_t j = sj; j < sj2; j += 4)
			*(block_4*)&left[j] = *(block_4*)&right[j];
		for (size_t j = sj2; j < nCounts; ++j)
			left[j] = right[j];
	}
}

// 矩阵类模板
template <class T1>
class CLMatrixT
{
     
public:
	using obj = CLMatrixT<T1>;
	using ref = obj&;
	typedef std::vector<T1> MatrixLine;
	typedef std::vector<MatrixLine> Matrix;
	typedef std::initializer_list<MatrixLine> MatrixL;
protected:
#if CLMAT_USE_MEMPOOLS > 0
	Matrix& matrix;
#else
	Matrix matrix;
#endif
	size_t m_rows, m_cols;
	template<class TList>
	void set(size_t r, size_t c, const TList& m) {
     
		resize(r, c);
#if CLMAT_USE_SSE > 0
		if (matrixUseSSE) {
     
			for (size_t i = 0; i < r; ++i)
				::memcpy_sse(&matrix[i][0], &m[i][0], c);
			return;
		}
#endif
		for (size_t i = 0; i < r; ++i)
			for (size_t j = 0; j < c; ++j)
				matrix[i][j] = m[i][j];
		return;
	}
	void valid() {
     //extend line to full
		for (size_t i = 0; i < rows(); ++i)
			matrix[i].resize(cols(), 0);//逐层扩充
	}
	void print_(PCStr lpFlag = nullptr) const {
      
		size_t r = rows();
		size_t c = cols();
		const size_t precst = 6;   // 小数点后数据最多位数
		const double v6 = ::pow(10.0, precst), v_6 = ::pow(10.0, -((double)precst)), v_13 = ::pow(10.0, -((double)(precst * 2 + 1)));
		size_t n = 0;              // 数据小数点前最大位数
		size_t pre = 0;            // 小数点后数据位数
		size_t wid = 1;            // 控制字符宽度=n+pre+符号位+小数点位
		for (size_t i = 0; i < r; i++)
		{
     
			for (size_t j = 0; j < c; j++)
			{
     
				//计算整数位
				size_t nc = 0;
				double maxV = ::abs(double(matrix[i][j]));
				while (maxV >= 1.0) {
     
					maxV /= 10.0;
					++nc;
				}

				//计算小数位
				auto xs = ((long long)(::abs(double(matrix[i][j] - ((T1)(long long)(matrix[i][j])))) * v6)) * v_6;
				size_t prec = 0;
				while (xs >= v_6) {
     
					xs *= 10.0;
					xs = xs - (double)(long long)xs + v_13;
					++prec;
					if (prec >= precst)
						break;
				}
				pre = max(pre, prec);
				auto widc = max(1, nc) + (prec > 0 ? prec + 1 : 0) + 1;
				//更新总位数
				wid = max(widc, wid);
			}
		}
		::_tprintf_s(_T("\nMatrix(%d,%d) %s = \n[\n"), (int)r, (int)c, lpFlag == 0 ? _T("") : lpFlag);
		cout << std::setiosflags(std::ios::fixed);
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				if (j > 0)
					cout << ",";
				if (::abs(double(matrix[i][j] - ((T1)(long long)(matrix[i][j])))) < v_6) //清除末尾全0
					cout << std::setprecision(0) << std::setw(wid) << matrix[i][j];
				else {
     
					//计算本元素实际小数位
					auto xs = ((long long)(::abs(double(matrix[i][j] - ((T1)(long long)(matrix[i][j])))) * v6)) * v_6;
					size_t prec = 0;
					while (xs >= v_6)
					{
     
						xs *= 10.0;
						xs = xs - (double)(long long)xs + v_13;
						++prec;
						if (prec >= precst)
							break;
					}
					cout << std::setprecision(prec) << std::setw(wid) << matrix[i][j];
				}
			}
			cout << endl;
		}
		printf_s("]\n");
		return;
		/*size_t i = 0, si = rows(), sj = cols();
		::_tprintf_s(_T("\nMatrix(%d,%d) %s = \n["), (int)si, (int)sj, lpFlag == 0 ? _T("") : lpFlag);
		double t = sizeof(T1) > 4 ? 1e-13 : 5e-5;
		for (; i < si; ++i)
		{
			printf_s("\n     ");
			for (size_t j = 0; j < sj; ++j)
			{
				if (j == 0)printf_s("%g", double(::abs(matrix[i][j]) < t ? 0 : matrix[i][j]));
				else printf_s(",  %g", double(::abs(matrix[i][j]) < t ? 0 : matrix[i][j]));
			}
		}
		printf_s("\n]\n");
		return *this;*/
	}
public:

#if CLMAT_USE_MEMPOOLS > 0
	static long long getMatrixCreateTimes() {
     
		return 0;
	}
	//默认构造
	CLMatrixT()
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     }
	~CLMatrixT() {
     
		giveUpOne(&matrix);
	}
	//带初值设定的矩阵构造
	CLMatrixT(size_t rows, size_t cols, T1 v = 0)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		resize(rows, cols, v);
	}
	//带自定义赋值模式的矩阵构造
	CLMatrixT(size_t rows, size_t cols, std::function<void(T1 & item, size_t row, size_t col)> const& func)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		make(rows, cols, func);
	}
	//带自定义赋值模式的方矩阵构造
	CLMatrixT(size_t siRank, std::function<void(T1 & item, size_t row, size_t col)> const& func)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		make(siRank, siRank, func);
	}
	CLMatrixT(const obj& m)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		//if (matrix.size() > 0)Sleep(0);
		*this = m;
	}
	template <class T2>	CLMatrixT(const CLMatrixT<T2>& m)
		: matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		*this = m;
	}
	CLMatrixT(const Matrix& m)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		*this = m;
	}

	CLMatrixT(const MatrixL& m)
		:matrix(*newOneAndNamed(Matrix, CLMatrixT_Inline_Matrix_Data)), m_rows(0), m_cols(0)
	{
     
		*this = m;
	}
#else
	static long long getMatrixCreateTimes() {
     
		return matrixCreateTimes;
	}
	//默认构造
	CLMatrixT() :m_rows(0), m_cols(0)
	{
     }
	~CLMatrixT() {
     
		matrixCreateTimes++;
	}
	//带初值设定的矩阵构造
	CLMatrixT(size_t rows, size_t cols, T1 v = 0) :m_rows(0), m_cols(0)
	{
     
		resize(rows, cols, v);
	}
	//带自定义赋值模式的矩阵构造
	CLMatrixT(size_t rows, size_t cols, std::function<void(T1 & item, size_t row, size_t col)> const& func) :m_rows(0), m_cols(0)
	{
     
		make(rows, cols, func);
	}
	//带自定义赋值模式的方矩阵构造
	CLMatrixT(size_t siRank, std::function<void(T1 & item, size_t row, size_t col)> const& func) :m_rows(0), m_cols(0)
	{
     
		make(siRank, siRank, func);
	}
	CLMatrixT(const obj& m) :m_rows(0), m_cols(0)
	{
     
		*this = m;
	}
	template <class T2>	CLMatrixT(const CLMatrixT<T2>& m) : m_rows(0), m_cols(0)
	{
     
		*this = m;
	}
	CLMatrixT(const Matrix& m) :m_rows(0), m_cols(0)
	{
     
		*this = m;
	}

	CLMatrixT(const MatrixL& m) :m_rows(0), m_cols(0)
	{
     
		*this = m;
	}
#endif
	//打开关闭sse指令加速
	static bool setUseSSE(bool open = true) {
     
		auto setbk = matrixUseSSE;
		matrixUseSSE = open;
		return setbk;
	}
	//获得sse指令加速开关值
	static bool isUseSSE() {
     
		return matrixUseSSE;
	}
	//设置SSE加速的最小的矩阵宽度
	static size_t setUseSSEMinRank(size_t rank = 10) {
     
		auto matrixUseSSEMinRankbk = matrixUseSSEMinRank;
		matrixUseSSEMinRank = rank;
		return matrixUseSSEMinRankbk;
	}
	ref operator=(const obj& m) {
     
		set(m.rows(), m.cols(), m.matrix);
		return *this;
	}
	template <class T2>	ref operator=(const CLMatrixT<T2>& m) {
     
		auto r = m.rows(), c = m.cols();
		resize(r, c);
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] = T1(m[i][j]);
			}
		}
		return *this;
	}
	ref operator=(const Matrix& m) {
     
		if ((m_rows = m.size()) > matrix.size()) {
     
			matrix.resize(m_rows);
		}
		m_cols = 0;
		for (size_t i = 0; i < m_rows; ++i)
		{
     
			if (m_cols < m[i].size())
				m_cols = m[i].size();
			matrix[i] = m[i];
		}
		valid();
		return *this;
	}
	ref operator=(const MatrixL& m) {
     
		if ((m_rows = m.size()) > matrix.size()) {
     
			matrix.resize(m_rows);
		}
		m_cols = 0;
		size_t i = 0;
		for (auto it = m.begin(); it != m.end(); ++it)
		{
     
			if (m_cols < (*it).size())
				m_cols = (*it).size();
			matrix[i] = *it;
			++i;
		}
		valid();
		return *this;
	}
	// 输出矩阵元素内容到控制台，参数可传入一个标识字符串
	void print(PCStr lpFlag = nullptr) const {
     
		return print_(lpFlag);
	}
	// 输出矩阵元素内容到控制台，参数可传入一个标识字符串
	ref print(PCStr lpFlag = nullptr) {
     		
		return print_(lpFlag), *this;
	}
	// 按指定规则构建矩阵,会按照指定规则修改每一项，方法区别于resize()
	ref make(size_t rows, size_t cols, std::function<void(T1 & item, size_t row, size_t col)> const& func = [](T1& v, size_t r, size_t c) {
      v = 0; }) {
     
		resize(rows, cols);
		auto r = this->rows(), c = this->cols();
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j) {
     
				func(matrix[i][j], i, j);
			}
		}
		return *this;
	}
	// 按指定规则构建矩阵,会按照指定规则修改每一项，方法区别于resize()
	ref make(size_t rows, size_t cols, T1 v = 0) {
     
		return make(rows, cols, [v](T1& i, size_t r, size_t c) {
      i = v; });
	}
	// 按指定规则构建方正矩阵（默认状态填充全0）
	ref makeSquare(size_t newRank, std::function<void(T1 & item, size_t row, size_t col)> const& func = [](T1& v, size_t r, size_t c) {
      v = 0; }) {
     
		return make(newRank, newRank, func);
	}
	// 按指定值填充构建方正矩阵并（默认状态填充全0）
	ref makeSquare(size_t newRank, T1 v = 0) {
     
		return make(newRank, newRank, [v](T1& i, size_t r, size_t c) {
      i = v; });
	}
	// 构建单位矩阵
	ref makeE(size_t newRank) {
     
		return makeSquare(newRank, [](T1& v, size_t r, size_t c) {
      if (r == c)v = 1; else v = 0; });
	}
	// 改变当前矩阵大小,用特定值填充,对已有的项不作调整
	ref resize(size_t rows, size_t cols, T1 v = 0)
	{
     
		if (rows > matrix.size()) {
     
			matrix.resize(rows);
			if (cols <= this->cols()) {
     
				for (size_t i = this->rows(); i < rows; ++i)
					matrix[i].resize(cols, v);
			}
			else {
     
				for (size_t i = 0; i < rows; ++i)
					matrix[i].resize(cols, v);
			}
		}
		else {
     
			if (cols > this->cols()) {
     
				for (size_t i = 0; i < rows; ++i)
					matrix[i].resize(cols, v);
			}
		}
		m_rows = rows;
		m_cols = cols;
		return *this;
	}
	// 取得一个填充或裁剪行后的新矩阵
	obj rerows(size_t newRows, T1 v = 0) const {
     
		obj m = *this;
		m.resize(newRows, cols(), v);
		return m;
	}
	// 取得一个填充或裁剪列后的新矩阵
	obj recols(size_t newCols, T1 v = 0) const {
     
		obj m = *this;
		m.resize(rows(), newCols, v);
		return m;
	}
	// 取得一个填充或裁剪行列后的新矩阵
	obj square(size_t newRank, T1 v = 0)const {
     
		obj m = *this;
		m.resize(newRank, newRank, v);
		return m;
	}
	// 取得一个按最大行或列数填充或裁剪行列后的新矩阵
	obj squareMax(T1 v = 0)const {
     
		auto r = max(rows(), cols());
		obj m = *this;
		m.resize(r, r, v);
		return m;
	}
	// 取得一个按最小行或列数填充或裁剪行列后的新矩阵
	obj squareMin(T1 v = 0)const {
     
		auto r = min(rows(), cols());
		obj m = *this;
		m.resize(r, r, v);
		return m;
	}
	// 在矩阵末尾添加一行,增加的行会被裁剪到列与矩阵一致，矩阵为空则直接增加，若矩阵不为空增加向量为空则增加一个全0向量到末尾
	ref add_row(const std::vector<T1>& Line)
	{
     		
		auto rs = rows();
		resize(rows() + 1, cols() > 0 ? cols() : Line.size());
		for (size_t i = 0; i < cols(); ++i)
		{
     
			if (i < Line.size())
				matrix[rs][i] = Line[i];
			else
				matrix[rs][i] = 0;
		}
		return *this;
	}
	// 在矩阵末尾添加一行数据,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref add_row(T1 v)
	{
     
		std::vector<T1> Line(cols(), v);
		return add_row(Line);
	}
	// 在矩阵末尾添加n行,增加的行会被裁剪到列与矩阵一致，矩阵为空则直接增加，若矩阵不为空增加向量为空则增加一个全0向量到末尾
	ref add_rows(const std::vector<T1>& Line, size_t nLine) {
     
		for (size_t l = nLine; l > 0; add_row(Line), --l);
		return *this;
	}
	// 在矩阵末尾添加n行数据,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref add_rows(T1 v, size_t nLine) {
     
		std::vector<T1> Line(cols(), v);
		return add_rows(Line, nLine);
	}
	// 在矩阵某行前添加一行数据，rowPos从0开始,若插入行大于总行数，则增加到矩阵末尾
	ref insert_row(const std::vector<T1>& Line, size_t rowPos) {
     
		if (rows() <= rowPos)
			return add_row(Line);
		auto cos = cols();
		auto it = matrix.insert(matrix.begin() + rowPos, Line);
		++m_rows;
		if (Line.size() > cos)
			it->erase(it->begin() + cos - 1, it->begin() + Line.size() - 1);
		else if (Line.size() < cos)
			it->resize(cos, 0);
		return *this;
	}
	// 在矩阵某行前添加一行数据，rowPos从0开始,若插入行大于总行数，则增加到矩阵末尾,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref insert_row(T1 v, size_t rowPos) {
     
		std::vector<T1> Line(cols(), v);
		return insert_row(Line, rowPos);
	}
	// 在矩阵某行前添加n行数据，rowPos从0开始,若插入行大于总行数，则增加到矩阵末尾
	ref insert_rows(const std::vector<T1>& Line, size_t rowPos, size_t nLine) {
     
		for (size_t l = nLine; l > 0; insert_row(Line, rowPos), --l);
		return *this;
	}
	// 在矩阵某行前添加n行数据，rowPos从0开始,若插入行大于总行数，则增加到矩阵末尾,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref insert_rows(T1 v, size_t rowPos, size_t nLine) {
     
		std::vector<T1> Line(cols(), v);
		return insert_rows(Line, rowPos, nLine);
	}
	//删除第rowPos行，rowPos从0开始
	ref delete_row(size_t rowPos) {
     
		auto cos = cols();
		if (cos > 0) {
     
			auto ros = rows();
			if (rowPos + 1 <= ros) {
     
				matrix.erase(matrix.begin() + rowPos);
				m_rows--;
			}
			if (rows() == 0)clear();
		}
		return *this;
	}
	//删除第rowPos开始计算的nLine行，rowPos从0开始,超出范围则删除从开始位置到末尾的全部行
	ref delete_rows(size_t rowPos, size_t nLine) {
     
		auto cos = cols();
		if (cos > 0 && nLine > 0) {
     
			auto ros = rows();
			if (rowPos + nLine <= ros)
				matrix.erase(matrix.begin() + rowPos, matrix.begin() + rowPos + nLine), m_rows -= nLine;
			else if (rowPos < ros)
				matrix.erase(matrix.begin() + rowPos, matrix.end()), m_rows -= (ros - rowPos);
			if (rows() == 0)clear();
		}
		return *this;
	}
	// 将换两行
	ref swap_row(size_t row1, size_t row2)
	{
     
		if (row1 != row2 && row1 >= 0 &&
			row1 < rows() && row2 >= 0 && row2 < rows())
		{
     
			std::swap(matrix[row1], matrix[row2]);
		}
		return *this;
	}         // 将换两行的数据
	// 在矩阵末尾添加一列,增加的列会被裁剪到列与矩阵一致，矩阵为空则直接增加，若矩阵不为空增加向量为空则增加一个全0向量到末尾
	ref add_col(const std::vector<T1>& line)
	{
     
		if(isEmpty())
			resize(line.size(), 1);
		else
			resize(rows(), cols() + 1);
		for (size_t i = 0; i < rows(); ++i)
		{
     
			if (i < line.size())
				matrix[i][cols() - 1] = line[i];
			else
				matrix[i][cols() - 1] = 0;
		}
		return *this;
	}
	// 在矩阵末尾添加一列数据,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref add_col(T1 v)
	{
     
		std::vector<T1> Line(rows(), v);
		return add_col(Line);
	}
	// 在矩阵末尾添加n列,增加的列会被裁剪到列与矩阵一致，矩阵为空则直接增加，若矩阵不为空增加向量为空则增加一个全0向量到末尾
	ref add_cols(const std::vector<T1>& Line, size_t nLine) {
     
		for (size_t i = 0; i < nLine; ++i)
			add_col(Line);
		return *this;
	}
	// 在矩阵末尾添加n列数据,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref add_cols(T1 v, size_t nLine) {
     
		std::vector<T1> Line(rows(), v);
		return add_cols(Line, nLine);
	}
	// 在矩阵某列前添加一列数据，rowPos从0开始,若插入列大于总列数，则增加到矩阵末尾
	ref insert_col(const std::vector<T1>& Line, size_t colPos) {
     
		if (cols() <= colPos)
			return add_col(Line);
		if (Line.size()) {
     
			auto ros = rows();
			size_t si = min(ros, Line.size());
			for (size_t i = 0; i < si; ++i)
				matrix[i].insert(matrix[i].begin() + colPos, Line[i]);
			for (size_t i = si; i < ros; ++i)
				matrix[i].insert(matrix[i].begin() + colPos, 0);
		}
		return *this;
	}
	// 在矩阵某列前添加一列数据，rowPos从0开始,若插入列大于总列数，则增加到矩阵末尾,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref insert_col(T1 v, size_t colPos) {
     
		std::vector<T1> Line(rows(), v);
		return insert_col(Line, colPos);
	}
	// 在矩阵某列前添加n列数据，rowPos从0开始,若插入列大于总列数，则增加到矩阵末尾
	ref insert_cols(const std::vector<T1>& Line, size_t colPos, size_t nLine) {
     
		if (cols() <= colPos)
			return add_cols(Line, nLine);
		if (Line.size() && nLine) {
     
			auto ros = rows();
			size_t si = min(ros, Line.size());
			for (size_t i = 0; i < si; ++i)
				matrix[i].insert(matrix[i].begin() + colPos, nLine, Line[i]);
			for (size_t i = si; i < ros; ++i)
				matrix[i].insert(matrix[i].begin() + colPos, nLine, 0);
		}
		return *this;
	}
	// 在矩阵某列前添加n列数据，rowPos从0开始,若插入列大于总列数，则增加到矩阵末尾,用值v初始化，若矩阵本身是一个空矩阵则什么也不做
	ref insert_cols(T1 v, size_t colPos, size_t nLine) {
     
		std::vector<T1> Line(rows(), v);
		return insert_cols(Line, colPos, nLine);
	}
	//删除第rowPos列，rowPos从0开始
	ref delete_col(size_t colPos) {
     
		auto col = cols();
		if (col > 0) {
     
			auto ros = rows();
			if (colPos + 1 <= col)
				for (size_t i = 0; i < ros; ++i)
					matrix[i].erase(matrix[i].begin() + colPos);
			if (cols() == 0)clear();
		}
		return *this;
	}
	//删除第rowPos开始计算的nLine列，rowPos从0开始,超出范围则删除从开始位置到末尾的全部列
	ref delete_cols(size_t colPos, size_t nLine) {
     
		auto col = cols();
		if (col > 0 && nLine > 0) {
     
			auto ros = rows();
			if (colPos + nLine <= col)
				for (size_t i = 0; i < ros; ++i)
					matrix[i].erase(matrix[i].begin() + colPos, matrix[i].begin() + colPos + nLine);
			else if (colPos < col)
				for (size_t i = 0; i < ros; ++i)
					matrix[i].erase(matrix[i].begin() + colPos, matrix[i].end());
			if (cols() == 0)clear();
		}
		return *this;
	}
	// 将换两列数据
	ref swap_col(size_t col1, size_t col2)
	{
     
		auto col = cols();
		if (col1 != col2 && col1 >= 0 && col1 < col && col2 >= 0 && col2 < col)
		{
     
			auto ros = rows();
			for (size_t i = 0, si = ros; i < si; ++i)
			{
     
				std::swap(matrix[i][col1], matrix[i][col2]);
			}
		}
		return *this;
	}
	// 用目标向量设置某一行，不会改变维度，多余元素省略
	ref setRow(size_t row, const std::vector<T1>& tag) {
     
		if (row < rows()) {
     
			auto& r = matrix[row];
			auto c = cols(); size_t i = 0;
			for (size_t si = min(c, tag.size()); i < si; ++i)
				r[i] = tag[i];
			for (; i < c; ++i)
				r[i] = 0;
		}
		return *this;
	}
	// 用目标向量设置某一列，不会改变维度，多余元素省略
	ref setCol(size_t col, const std::vector<T1>& tag) {
     
		if (col < cols()) {
     
			auto r = rows(); size_t i = 0;
			for (size_t si = min(r, tag.size()); i < si; ++i)
				matrix[i][col] = tag[i];
			for (; i < r; ++i)
				matrix[i][col] = 0;
		}
		return *this;
	}
	// 从一维向量数据初始化矩阵，数据不够则填充0
	ref getFromVector(const std::vector<T1>& tag) {
     
		auto r = rows(), c = cols();
		size_t tt = 0, stt = tag.size();
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				if (tt < stt)
					matrix[i][j] = tag[tt++];
				else
					matrix[i][j] = 0;
			}
		}
		return *this;
	}
	// 把矩阵拆解到一个一维向量
	std::vector<T1>& setToVector(std::vector<T1>& tag) const {
     
		auto r = rows(), c = cols();
		tag.resize(r * c);
		size_t tt = 0, stt = tag.size();
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				tag[c * i + j] = matrix[i][j];
			}
		}
		return tag;
	}
	// 清理矩阵
	ref clear()
	{
     
		m_rows = m_cols = 0;
		return *this;
	}
	// 通过自定义方式修改矩阵中的每项，也可只修改一个子矩阵区域。若只是需要修改一份矩阵的副本请使用operate()方法。
	ref reset(std::function<void(T1 & item, size_t iRow, size_t iCol)> const& func,
		size_t startRow = 0, size_t startCol = 0, size_t endRow = 0, size_t endCol = 0)
	{
     
		return ::reset(*this, func, startRow, startCol, endRow, endCol);
	}
	// 设置矩阵为特定值，也可只设置一个子矩阵区域
	ref reset(T1 v, size_t startRow = 0, size_t startCol = 0, size_t endRow = 0, size_t endCol = 0) {
     
		//lambda捕获参数v赋值给每一项
		return reset([v](T1& i, size_t ro, size_t co) {
     	i = v; },
			startRow, startCol, endRow, endCol);
	}
	// 矩阵置0
	ref zero() {
      return reset(0); }
	// 拷贝并逐项操作函数，若是需要修改原矩阵请使用reset()方法。
	// 作用：取得原矩阵的拷贝并按规则处理每一项后的新矩阵（默认状态下只拷贝什么也不做），也可设定范围让规则只作用于一个子区域
	obj operate(std::function<void(T1 & item, size_t iRow, size_t iCol)> const& func = [](T1&, size_t, size_t) {
     },
		size_t startRow = 0, size_t startCol = 0, size_t endRow = 0, size_t endCol = 0) const {
     
		obj m = *this;
		return ::reset(m, func, startRow, startCol, endRow, endCol);
	}
	ref operator--() {
     
		return operator-=(1);
	}
	ref operator++() {
     
		return operator+=(1);
	}
	obj operator--(int) {
     
		obj m = *this;
		operator-=(1);
		return m;
	}
	obj operator++(int) {
     
		obj m = *this;
		operator+=(1);
		return m;
	}
	// 矩阵的行数
	size_t  rows() const {
      return /*matrix.size() */ m_rows; }
	// 矩阵的列数
	size_t  cols() const {
      return /*matrix.size() ? matrix[0].size() : 0*/ m_cols; }
	// 是否为空
	bool isEmpty() const {
      return rows() == 0; }
	// 是否为方阵
	bool isSquare() const {
      return (!(isEmpty()) && (rows() == cols())); }
	// 是否有无效元素
	bool isInvalid(size_t* row = nullptr, size_t* col = nullptr) const {
     
		for (size_t i = 0; i < rows(); ++i)
		{
     
			auto& lay = matrix[i];
			for (size_t j = 0; j < cols(); ++j)
			{
     
				if (_isnan(lay[j]) || isinf(lay[j])) {
     
					if (row)*row = i;
					if (col)*col = j;
					return true;
				}
			}
		}
		return false;
	}
	// 出现无效元素，打印并抛出异常
	const ref invalidPrintAndThrow() const {
     
		if (isInvalid()) {
     
			this->print(_T(""));
			throw std::runtime_error("Invalid Matrix");
		}
		return *this;
	}
	ref invalidPrintAndThrow() {
     
		if (isInvalid()) {
     
			this->print(_T(""));
			throw std::runtime_error("Invalid Matrix");
		}
		return *this;
	}
	//[]操作符重载 
	const MatrixLine& operator[](size_t row) const {
      return matrix[row]; }
	//[]操作符重载 
	MatrixLine& operator[](size_t row) {
      return matrix[row]; }

	template <class T2>	obj& operator+=(const CLMatrixT<T2>& m)
	{
     
#if CLMAT_USE_SSE > 0
		if (matrixUseSSE)
			return ::matrixAddSelf(*this, m);
#endif // UseSSE
		size_t r = min(rows(), m.rows());
		size_t c = min(cols(), m.cols());
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] += m[i][j];
			}
		}
		return *this;
	}
	obj& operator+=(T1 v)
	{
     
		size_t r = rows();
		size_t c = cols();
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] += v;
			}
		}
		return *this;
	}
	template <class T2> obj& operator-=(const CLMatrixT<T2>& m)
	{
     
#if CLMAT_USE_SSE > 0
		if (matrixUseSSE)
			return ::matrixSubSelf(*this, m);
#endif // UseSSE
		size_t r = min(rows(), m.rows());
		size_t c = min(cols(), m.cols());

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] -= m[i][j];
			}
		}

		return *this;
	}
	obj& operator-=(T1 v)
	{
     
		return *this += (-v);
	}
	template <class T2> obj& operator*=(const CLMatrixT<T2>& m)
	{
     
		return *this = ::dotMul(*this, m, (ref)obj());
	}
	obj& operator*=(T1 v)
	{
     
		size_t r = rows();
		size_t c = cols();

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] *= v;
			}
		}
		return *this;
	}
	template <class T2> obj& operator/=(const CLMatrixT<T2>& m)
	{
     
		return operator*=(::inv(m, (ref)obj()));
	}
	obj& operator/=(T1 v)
	{
     
		size_t r = rows();
		size_t c = cols();

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] /= v;
			}
		}
		return *this;
	}
	obj& operator%=(const int v)
	{
     
		size_t r = rows();
		size_t c = cols();

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				matrix[i][j] %= v;
			}
		}
		return *this;
	}
	// 矩阵拷贝后每个元素取指数
	obj pow(T1 v) const
	{
     
		size_t r = rows();
		size_t c = cols();
		obj m(r, c);

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				m[i][j] = ::pow(matrix[i][j], v);
			}
		}
		return m;
	}
	// 矩阵拷贝后每个元素做为底数base的指数计算每一项
	obj powSelf(T1 base) const
	{
     
		size_t r = rows();
		size_t c = cols();
		obj m(r, c);
		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				m[i][j] = ::pow(base, matrix[i][j]);
			}
		}
		return m;
	}
	// 矩阵拷贝后每个元素取e为底数的幂
	obj exp() const
	{
     
		size_t r = rows();
		size_t c = cols();
		obj m(r, c);

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				m[i][j] = ::exp(matrix[i][j]);
			}
		}
		return m;
	}
	// 矩阵拷贝后每个元素开根
	obj sqrt() const
	{
     
		size_t r = rows();
		size_t c = cols();
		obj m(r, c);

		for (size_t i = 0; i < r; ++i)
		{
     
			for (size_t j = 0; j < c; ++j)
			{
     
				m[i][j] = ::sqrt(matrix[i][j]);
			}
		}
		return m;
	}
	// 对矩阵的所有元素求和
	T1 sum() const {
     
		auto r = rows(), c = cols();
		T1 ret = 0;
		for (size_t i = 0; i < r; ++i)
			for (size_t j = 0; j < c; ++j)
				ret += matrix[i][j];
		return ret;
	}
	// 对矩阵的每一行分别求和，得到N行1列矩阵，结果矩阵每行保存原矩阵每行元素相加之和
	obj sumRows() const {
     
		auto r = rows(), c = cols();
		if (r == 0)return obj();
		obj m(r, 1);
		for (size_t i = 0; i < r; ++i)
		{
     
			T1 sm = 0;
			for (size_t j = 0; j < c; ++j)
			{
     
				sm += matrix[i][j];
			}
			m[i][0] = sm;
		}
		return m;
	}
	// 对矩阵的每一列分别求和，得到1行N列矩阵，结果矩阵每行保存原矩阵每列元素相加之和
	obj sumCols() const {
     
		auto r = rows(), c = cols();
		if (c == 0)return obj();
		obj m(1, c);
		for (size_t j = 0; j < c; ++j)
		{
     
			T1 sm = 0;
			for (size_t i = 0; i < r; ++i)
			{
     
				sm += matrix[i][j];
			}
			m[0][j] = sm;
		}
		return m;
	}
	//矩阵内积。满足左列=右行条件
	template <class T2> obj dotMul(const CLMatrixT<T2>& rhs) const {
     
		return ::dotMul(*this, rhs, (ref)obj());
	}
	//矩阵逐点相乘。当左右操作数的列数应该对应相同，且右操作数行必须为1或大于左操作数的行。
	template <class T2> obj mul(const CLMatrixT<T2>& rhs) const {
     
		return ::mul(*this, rhs, (ref)obj());
	}
	//矩阵逐点相乘,右操作数是按其转置来处理逐点相乘的。当右操作数的列数对应的左操作数行相同，且右操作数的列必须为1或大于左操作数的行。
	template <class T2> obj mul_T(const CLMatrixT<T2>& rhs) const {
     
		return ::mul_T(*this, rhs, (ref)obj());
	}
	//矩阵按列逐点相乘。当左右操作数的行数应该对应相同，且右操作数列必须为1或大于左操作数的列数。
	template <class T2> obj mul_V(const CLMatrixT<T2>& rhs) const {
     
		return ::mul_V(*this, rhs, (ref)obj());
	}
	//矩阵按列逐点相乘,右操作数是按其转置来处理逐点相乘的。当右操作数的行数对应的左操作数列相同，且右操作数的行必须为1或大于左操作数的列。
	template <class T2> obj mul_VT(const CLMatrixT<T2>& rhs) const {
     
		return ::mul_VT(*this, rhs, (ref)obj());
	}
	template<class T2> obj conv(
		const CLMatrixT<T2>& K, //卷积核
		size_t _stepX = 1, //卷积核X移动步长
		size_t _stepY = 1, //卷积核Y移动步长
		size_t padding = 0,//输入map，即本矩阵的边缘填充宽度
		double paddingValue = 0.0 //输入map，即本矩阵边缘填充内所填充的值（该值不一定是0，根据计算需要自由设置）
	) const {
     
		return ::conv(*this, K, (ref)obj(), _stepX, _stepY, padding, paddingValue);
	}
	// 是否是奇异矩阵
	bool isSingularMatrix() const
	{
     
		double detA = det();
		if (detA < 1e-15 && detA > -1e-15)
			return true;
		else return false;
	}
	// 求矩阵行列式
	T1 det() const
	{
     
		return ::det(*this);
	}
	// 求矩阵的子矩阵行列式
	T1 det(size_t start, size_t end) const
	{
     
		return ::det(*this, start, end);
	}
	// 求矩阵的绝对值矩阵
	obj abs() const
	{
     
		return ::abs(*this, (ref)obj());
	}
	//将一个矩阵变换到对角线矩阵，同一行和同一列的值都加到主对角上
	obj diag() const {
     
		return ::diag(*this, (ref)obj());
	}
	// 矩阵的最大元素值
	T1 maxElement() const
	{
     
		return ::maxElement(*this);
	}
	// 矩阵最大元素值及其所在的行和列
	T1 maxElement(size_t& row, size_t& col) const
	{
     
		return ::maxElement(*this, row, col);
	}
	// 矩阵的最小元素值
	T1 minElement() const
	{
     
		return ::minElement(*this);
	}
	// 矩阵最小元素值及其所在的行和列
	T1 minElement(size_t& row, size_t& col) const
	{
     
		return ::minElement(*this, row, col);
	}
	// 矩阵的转置矩阵
	obj T() const
	{
     
		return ::T(*this, (ref)obj());
	}
	// 将对象自身转置
	obj& makeT() {
     
		auto r = rows(), c = cols();
		auto mi = min(r, c);
		resize(c, r);
		for (size_t i = 0; i < mi; ++i)
			for (size_t j = 0; j < i; ++j)
				swap(matrix[i][j], matrix[j][i]);
		if (r > c) {
     
			for (size_t i = mi; i < r; ++i)
				for (size_t j = 0; j < c; ++j)
					swap(matrix[i][j], matrix[j][i]);
		}
		else if (r < c) {
     
			for (size_t i = 0; i < r; ++i)
				for (size_t j = mi; j < c; ++j)
					swap(matrix[i][j], matrix[j][i]);
		}
		return *this;
	}
	// 矩阵的子矩阵。rb开始行，re结束行，cb开始列，ce结束列。
	obj submatrix(size_t rb, size_t cb, size_t re, size_t ce) const
	{
     
		return ::submatrix(*this, rb, cb, re, ce, (ref)obj());
	}
	// 矩阵的逆矩阵，要求原矩阵不为空且为方矩阵
	obj inv() const
	{
     
		return ::inv(*this, (ref)obj());
	}
	// 计算方阵 M 的 LU 分解,取得增广和矩阵
	obj LU() const
	{
     
		return ::LU(*this, (ref)obj());
	}
	// 计算方阵 M 的 LU 分解,使得 M = LU;其中L为对角线元素全为1的下三角阵，U为对角元素依赖M的上三角阵
	// LU相乘后结果可能存在行或列的位置变换，但不改变矩阵原有性质
	bool LU(ref L, ref U) const {
     
		return ::LU(*this, L, U);
	}
	// 从输入流读取矩阵
	bool readMatrix(istream& in /*= std::cin */)
	{
     
		*this = ::readMatrix(in);
		if (this->rows() > 0 && this->cols() > 0)
			return true;
		else return false;
	}
	// 从输入流读取矩阵
	bool readMatrix(const tstring& file)
	{
     
		::readMatrix(*this, file);
		if (this->rows() > 0 && this->cols() > 0)
			return true;
		else return false;
	}
	// 从二进制文件load矩阵
	bool loadMatrix(const tstring& file)
	{
     
		::loadMatrix(*this, file);
		if (this->rows() > 0 && this->cols() > 0)
			return true;
		else return false;
	}
	// 将矩阵输出到指定输出流
	void printMatrix(ostream& out /*= std::_tprintf_s */) const
	{
     
		::printMatrix(*this, out);
	}
	// 将矩阵输出到指定输出流
	void printMatrix(const tstring& file) const
	{
     
		::printMatrix(*this, file);
	}
	// 将矩阵数据存为二进制文件 
	void saveMatrix(const tstring& file) const
	{
     
		::saveMatrix(*this, file);
	}
	//回调函数标准形式，v项的引用，r为行标，c为列标
	typedef void (*PInitMatrix)(T1& v, size_t r, size_t c);
	static void initE(T1& v, size_t r, size_t c) {
     
		if (r == c) v = T1(1);
		else v = T1(0);
	};
	static void initRand_F_0_1(T1& v, size_t r, size_t c) {
     
		v = T1(double(rand()) / RAND_MAX);
	};
	static void initRand_F_0_10(T1& v, size_t r, size_t c) {
     
		v = T1(double(rand()) / RAND_MAX * 10);
	};
	static void initRand_F_f1_1(T1& v, size_t r, size_t c) {
     
		v = T1(double(rand()) / RAND_MAX * 2 - 1);
	};
	static void initRand_F_f10_10(T1& v, size_t r, size_t c) {
     
		v = T1(double(rand()) / RAND_MAX * 20 - 10);
	};
	static void initRand_I_10(T1& v, size_t r, size_t c) {
     
		v = T1(rand() % 10);
	};
	static void initRand_I_100(T1& v, size_t r, size_t c) {
     
		v = T1(rand() % 100);
	};
	static void initRand_I_f10_10(T1& v, size_t r, size_t c) {
     
		v = T1(int(rand() % 20) - 10);
	};
	static void initRand_I_f100_100(T1& v, size_t r, size_t c) {
     
		v = T1(int(rand() % 200) - 100);
	};
	static obj E(size_t rank) {
     
		return obj(rank, initE);
	}
};

// 通过自定义方式修改矩阵中的每项，也可只修改一个子矩阵区域
template<class T1> CLMatrixT<T1>& reset(CLMatrixT<T1>& m, std::function<void(T1 & item, size_t iRow, size_t iCol)> const& func,
	size_t startRow = 0, size_t startCol = 0, size_t endRow = 0, size_t endCol = 0)
{
     
	size_t i = min(startRow, endRow), j = min(startCol, endCol);
	size_t i2 = max(startRow, endRow) == 0 ? m.rows() : min(max(startRow, endRow), m.rows());
	size_t j2 = max(startCol, endCol) == 0 ? m.cols() : min(max(startCol, endCol), m.cols());
	for (size_t r = i; r < i2; r++)
	{
     
		for (size_t c = j; c < j2; c++)
			func(m[r][c], r, c);
	}
	return m;
}
// 矩阵转置
template<class T1, class T2> CLMatrixT<T2>& T(const CLMatrixT<T1>& m, CLMatrixT<T2>& ret)
{
     
	if (m.isEmpty()) return ret.clear();
	size_t row = m.cols();
	size_t col = m.rows();
	ret.resize(row, col);
	for (size_t i = 0; i < row; ++i)
	{
     
		for (size_t j = 0; j < col; ++j)
		{
     
			ret[i][j] = T2(m[j][i]);
		}
	}
	return ret;
}
#ifdef _WINDOWS_
#define _CLMatrixT_Runtime_Error_Box(err) ::MessageBoxA(nullptr, (err), "CLMatrixT Runtime Error", MB_ICONERROR);
#else
#define _CLMatrixT_Runtime_Error_Box(err)
#endif
// 计算方阵行列式
template<class T1> T1 det(const CLMatrixT<T1>& m)
{
     
	if (m.isEmpty())
	{
     
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" det \", matix obj is empty matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:det");
	}
	else if (!m.isSquare()) {
     
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" det \", matix obj is not a square matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:det");
	}
	T1 ret = 0;

	CLMatrixT<T1> N;
	LU(m, N);

	if (N.isEmpty()) return ret;

	ret = 1.0;
	for (size_t i = 0; i < N.cols(); ++i)
	{
     
		ret *= N[i][i];
	}

	if (isSignRev(N[N.rows() - 1]))
	{
     
		return -ret;
	}

	return ret;
}
// 计算矩阵指定子方阵的行列式 
template<class T1> T1 det(const CLMatrixT<T1>& m, size_t start, size_t end)
{
     
	return det(submatrix(m, start, end, start, end, CLMatrixT<T1>()));
}
// 计算绝对值
template<class T1, class T2> CLMatrixT<T2>& abs(const CLMatrixT<T1>& m, CLMatrixT<T2>& ret)
{
     
	if (m.isEmpty())
	{
     
		ret.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" abs \", matix obj is empty matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:abs");
	}
	size_t r = m.rows();
	size_t c = m.cols();
	ret.resize(r, c);
	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			T1 t = m[i][j];
			if (t < 0) ret[i][j] = T2(-t);
			else ret[i][j] = T2(t);
		}
	}
	return ret;
}
// 返回矩阵所有元素的最大值
template<class T1> T1 maxElement(const CLMatrixT<T1>& m)
{
     
	if (m.isEmpty()) return 0;

	T1 ret = m[0][0];
	size_t r = m.rows();
	size_t c = m.cols();

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (m[i][j] > ret)
				ret = m[i][j];
		}
	}
	return ret;
}
// 计算矩阵最大值，并返回该元素的引用
template<class T1> T1 maxElement(const CLMatrixT<T1>& m, size_t& row, size_t& col)
{
     
	if (m.isEmpty()) return 0.;

	T1 ret = m[0][0];
	row = 0;
	col = 0;

	size_t r = m.rows();
	size_t c = m.cols();

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (m[i][j] > ret)
			{
     
				ret = m[i][j];
				row = i;
				col = j;
			}
		}
	}
	return ret;
}
// 计算矩阵所有元素最小值
template<class T1> T1 minElement(const CLMatrixT<T1>& m)
{
     
	if (m.isEmpty()) return 0;

	T1 ret = m[0][0];
	size_t r = m.rows();
	size_t c = m.cols();

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (m[i][j] < ret) ret = m[i][j];
		}
	}

	return ret;
}
// 计算矩阵最小值，并返回该元素的引用
template<class T1> T1 minElement(const CLMatrixT<T1>& m, size_t& row, size_t& col)
{
     
	if (m.isEmpty()) return 0.;

	T1 ret = m[0][0];
	row = 0;
	col = 0;
	size_t r = m.rows();
	size_t c = m.cols();

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (m[i][j] < ret)
			{
     
				ret = m[i][j];
				row = i;
				col = j;
			}
		}
	}

	return ret;
}
// 取矩阵中指定位置的子矩阵。rb开始行，re结束行，cb开始列，ce结束列。
template<class T1, class T2> CLMatrixT<T2>& submatrix(const CLMatrixT<T1>& m, size_t _rb, size_t _cb, size_t _re, size_t _ce, CLMatrixT<T2>& ret)
{
     
	if (m.isEmpty()) return ret.clear();
	
	auto rb = min(min(_rb, _re), m.rows());
	auto re = min(max(_rb, _re)+1, m.rows());
	auto cb = min(min(_cb, _ce), m.cols());
	auto ce = min(max(_cb, _ce)+1, m.cols());

	if (rb == re || cb == ce) return ret.clear();

	ret.resize(re - rb, ce - cb);

	for (size_t i = rb; i < re; ++i)
	{
     
		for (size_t j = cb; j < ce; ++j)
		{
     
			ret[i - rb][j - cb] = T2(m[i][j]);
		}
	}

	return ret;
}
// 计算逆矩阵
template<class T1, class T2> CLMatrixT<T2>& inv(const CLMatrixT<T1>& m, CLMatrixT<T2>& ret)
{
     
	return LUP_Inverse(m, ret);
}
// 计算方阵 M 的 LU 分解,取得增广和矩阵
template<class T1, class T2> CLMatrixT<T2>& LU(const CLMatrixT<T1>& m, CLMatrixT<T2>& ret)
{
     
	if (m.isEmpty())
	{
     
		ret.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" LU \", matix obj is empty matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:LU");
	}
	else if (!m.isSquare()) {
     
		ret.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" LU \", matix obj is not a square matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:LU");
	}

	size_t n = m.rows();
	ret.resize(n + 1, n);

	for (size_t i = 0; i < n; ++i)
	{
     
		ret[n][i] = -1;
	}

	for (size_t i = 0; i < n; ++i)
	{
     
		for (size_t j = 0; j < n; ++j)
		{
     
			ret[i][j] = T2(m[i][j]);
		}
	}

	for (size_t k = 0; k < n - 1; ++k)
	{
     
		size_t p = max_idx(ret, k, n);
		if (p != k)              // 进行行交换
		{
     
			ret.swap_row(k, p);
			ret[n][k] = T2(p); // 记录将换信息
		}

		if (ret[k][k] == 0)
		{
     
			cout << endl << "[Runtime error]: Matrix is singular, unable to calculate inverse!" << endl;
			return ret.clear();
		}

		for (size_t i = k + 1; i < n; ++i)
		{
     
			ret[i][k] /= ret[k][k];
			for (size_t j = k + 1; j < n; ++j)
			{
     
				ret[i][j] -= ret[i][k] * ret[k][j];
			}
		}
	}

	return ret;
}
// 从输入流读取矩阵
template<class T1> CLMatrixT<T1>& readMatrix(CLMatrixT<T1>& M, istream& in = std::cin)
{
     
	M.clear();
	string str;
	T1 b;
	//CLMatrixT::MatrixLine v;
	size_t i = 0, r = 0, c = 0;
	while (getline(in, str))
	{
     
		for (string::size_type i = 0; i < str.size(); ++i)
		{
     
			if (str[i] == ',' || str[i] == ';')
			{
     
				str[i] = ' ';
			}
			else if (str[i] != '.' && (str[i] < '0' || str[i] > '9')
				&& str[i] != ' ' && str[i] != '\t' && str[i] != '-')
			{
     
				M.clear();
				return M;
			}
		}
		istringstream sstream(str);
		if (++i == 1) {
     
			sstream >> r >> c;
			M.make(r, c, 0);
			r = M.rows(), c = M.cols();
			continue;
		}
		if (i - 2 < r) {
     
			for (size_t j = 0; j < c; ++j)
			{
     
				if (sstream >> b)
					M[i - 2][j] = b;
			}
		}
	}
	return M;
}               // 从指定输入流读入矩阵
// 从文本文件读入矩阵
template<class T1> CLMatrixT<T1>& readMatrix(CLMatrixT<T1>& M, const tstring& file)
{
     
	ifstream fin(file.c_str());
	if (!fin)
	{
     
		//cerr << "Error: open file " << file << " failed." << endl;
		return M.clear();
	}
	readMatrix(M, (istream&)fin);
	fin.close();
	return M;
}                          // 从文本文件读入矩阵
// 从二进制文件load矩阵
template<class T1> CLMatrixT<T1>& loadMatrix(CLMatrixT<T1>& m, const tstring& file)
{
     
	ifstream fin(file.c_str(), std::ios_base::in | std::ios::binary);
	if (!fin) return m.clear();

	char Flag[14];
	fin.read((char*)&Flag, sizeof(Flag));

	string str(Flag);
	if (str != "CLMATRIX_DATA")
	{
     
		return m.clear();
	}

	int r, c;
	fin.read((char*)&r, sizeof(r));
	fin.read((char*)&c, sizeof(c));

	if (r <= 0 || c <= 0) return m.clear();

	m.resize(r, c);
	double t;

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			fin.read((char*)&t, sizeof(t));
			m[i][j] = T1(t);
		}
	}

	return m;
}                          // 从二进制文件读取矩阵
// 将矩阵输出到指定输出流
template<class T1> void  printMatrix(const CLMatrixT<T1>& m, ostream& out = std::cout)
{
     
	size_t r = m.rows();
	size_t c = m.cols();

	size_t n = 0;              // 数据小数点前最大位数
	double ma = (double)::maxElement(m);
	double mi = (double)::minElement(m);

	double maxV = max(::abs(ma), ::abs(mi));
	while (maxV >= 1.0)
	{
     
		maxV /= 10;
		++n;
	}
	if (n == 0) n = 1;    // 如果最大数绝对值小于1，这小数点前位数为1，为数字0
	size_t pre = 6;            // 小数点后数据位数
	size_t wid = n + pre + 3;  // 控制字符宽度=n+pre+符号位+小数点位

	out << std::setiosflags(std::ios::fixed);
	out << std::setw(wid) << r << std::setw(wid) << c << endl;
	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if(::abs(double(m[i][j] - ((T1)(long long)(m[i][j])))) < 1e-6)
				out << std::setprecision(0) << std::setw(wid)  <<  m[i][j];
			else 
				out << std::setprecision(pre) << std::setw(wid) <<  m[i][j];
		}
		out << endl;
	}
	out << std::setprecision(6);
}  // 从指定输出流打印矩阵
// 将矩阵打印到指定文件 
template<class T1> void  printMatrix(const CLMatrixT<T1>& m, const tstring& file)
{
     
	ofstream fout(file.c_str());
	if (!fout) return;

	printMatrix(m, fout);
	fout.close();
}                // 将矩阵输出到文本文件
// 将矩阵数据存为二进制文件 
template<class T1> void  saveMatrix(const CLMatrixT<T1>& m, const tstring& file)
{
     
	if (m.isEmpty()) return;

	ofstream fout(file.c_str(), std::ios_base::out | std::ios::binary);
	if (!fout) return;

	int r = m.rows();
	int c = m.cols();
	char Flag[14] = "CLMATRIX_DATA";
	fout.write((char*)&Flag, sizeof(Flag));
	fout.write((char*)&r, sizeof(r));
	fout.write((char*)&c, sizeof(c));

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			double t = m[i][j];
			fout.write((char*)&t, sizeof(t));
		}
	}

	fout.close();
}                 // 将矩阵保存为二进制文件

template<class T1, class T2>
bool  operator==(const CLMatrixT<T1>& lhs, const CLMatrixT<T2>& rhs)
{
     
	auto r = lhs.rows(), c = lhs.cols();
	if (r != rhs.rows() || c != rhs.cols())
	{
     
		return false;
	}

	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (lhs[i][j] != T1(rhs[i][j]))
			{
     
				return false;
			}
		}
	}

	return true;
}
template<class T1, class T2>
bool  operator==(const CLMatrixT<T1>& lhs, T2 v)
{
     
	auto r = lhs.rows(), c = lhs.cols();
	if (r == 0 || c == 0)
	{
     
		return false;
	}
	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (lhs[i][j] != T1(v))
			{
     
				return false;
			}
		}
	}
	return true;
}
template<class T1, class T2>
bool  operator==(T2 v, const CLMatrixT<T1>& lhs)
{
     
	return lhs == v;
}
template<class T1, class T2>
bool  operator!=(const CLMatrixT<T1>& lhs, const CLMatrixT<T2>& rhs)
{
     
	return !(lhs == rhs);
}
template<class T1, class T2>
bool  operator!=(const CLMatrixT<T1>& lhs, T2 v)
{
     
	return !(lhs == v);
}
template<class T1, class T2>
bool  operator!=(T2 v, const CLMatrixT<T1>& lhs)
{
     
	return !(lhs == v);
}
template<class T1, class T2>
CLMatrixT<T1> operator+(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs)
{
     
	auto m = lhs;
	m += rhs;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator+(const  CLMatrixT<T1>& lhs, T2 v)
{
     
	auto m = lhs;
	m += v;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator+(T2 v, const  CLMatrixT<T1>& lhs)
{
     
	auto m = lhs;
	m += v;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator-(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs)
{
     
	auto m = lhs;
	m -= rhs;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator-(const  CLMatrixT<T1>& lhs, T2 v)
{
     
	auto m = lhs;
	m -= v;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator-(T2 v, const  CLMatrixT<T1>& lhs)
{
     
	return lhs * (-1) + v;
}

//以下在window平台使用PPL加速
#ifdef _WINDOWS_
#include "ppl.h" //windows ppl
using namespace Concurrency;
#ifndef CLMAT_USE_CXX_PPL
#define CLMAT_USE_CXX_PPL 1  //打开PPL
#define DOTMUL_RANK_LIMIT 80 //可调参，及其性能不同调整，尽量在64-128间
#define DOTMUL_BLOCKS     32 //分块最小单元
#define CONV_RANK_LIMIT 32 //可调参，及其性能不同调整，尽量在32-128间，卷积运算单元过程复杂，设置阶数可降低
#define CONV_BLOCKS     16 //分块最小单元
#endif
#endif

#if CLMAT_USE_SSE > 0

#include 
#include 

#define CLMAT_FLOAT_USEAVX 1 //float 采用256bit AVX

//sse逐点相+
inline void lineAdd_sse(const float* left, const float* right, int nCounts, float* save) {
     
#if CLMAT_FLOAT_USEAVX > 0
	for (int k = nCounts - 8; k >= 0; k -= 8)  // do every 8 elements 
		_mm256_storeu_ps(save + k, _mm256_add_ps(_mm256_loadu_ps(left + k), _mm256_loadu_ps(right + k)));
	for (int k = (nCounts % 8) - 4; k >= 0; k -= 4)  // do every 4 elements 
#else
	for (int k = nCounts - 4; k >= 0; k -= 4)  // do every 4 elements 
#endif
		_mm_storeu_ps(save + k, _mm_add_ps(_mm_loadu_ps(left + k), _mm_loadu_ps(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] + right[k];
}
inline void lineAdd_sse(const double* left, const double* right, int nCounts, double* save) {
     
	for (int k = nCounts - 4; k >= 0; k -= 4)  // sum every 4 elements 
		_mm256_storeu_pd(save + k, _mm256_add_pd(_mm256_loadu_pd(left + k), _mm256_loadu_pd(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] + right[k];
}
template<class T1, class T2>  CLMatrixT<T1>& matrixAddSelf(CLMatrixT<T1>& m, const CLMatrixT<T2>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		for (size_t j = 0; j < c; ++j)
			m[i][j] += rhs[i][j];
	return m;
}
template<>inline  CLMatrixT<float>& matrixAddSelf(CLMatrixT<float>& m, const CLMatrixT<float>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		lineAdd_sse(&m[i][0], &rhs[i][0], (int)c, &m[i][0]);
	return m;
}
template<>inline  CLMatrixT<double>& matrixAddSelf(CLMatrixT<double>& m, const CLMatrixT<double>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		lineAdd_sse(&m[i][0], &rhs[i][0], (int)c, &m[i][0]);
	return m;
}
//sse逐点相-
inline void lineSub_sse(const float* left, const float* right, int nCounts, float* save) {
     
#if CLMAT_FLOAT_USEAVX > 0
	for (int k = nCounts - 8; k >= 0; k -= 8)  // do every 8 elements 
		_mm256_storeu_ps(save + k, _mm256_sub_ps(_mm256_loadu_ps(left + k), _mm256_loadu_ps(right + k)));
	for (int k = (nCounts % 8) - 4; k >= 0; k -= 4)  // do every 4 elements 
#else
	for (int k = nCounts - 4; k >= 0; k -= 4)  // do every 4 elements 
#endif
		_mm_storeu_ps(save + k, _mm_sub_ps(_mm_loadu_ps(left + k), _mm_loadu_ps(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] - right[k];
}
inline void lineSub_sse(const double* left, const double* right, int nCounts, double* save) {
     
	for (int k = nCounts - 4; k >= 0; k -= 4)  // sum every 4 elements 
		_mm256_storeu_pd(save + k, _mm256_sub_pd(_mm256_loadu_pd(left + k), _mm256_loadu_pd(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] - right[k];
}
template<class T1, class T2>  CLMatrixT<T1>& matrixSubSelf(CLMatrixT<T1>& m, const CLMatrixT<T2>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		for (size_t j = 0; j < c; ++j)
			m[i][j] -= rhs[i][j];
	return m;
}
template<>inline  CLMatrixT<float>& matrixSubSelf(CLMatrixT<float>& m, const CLMatrixT<float>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		lineSub_sse(&m[i][0], &rhs[i][0], (int)c, &m[i][0]);
	return m;
}
template<>inline  CLMatrixT<double>& matrixSubSelf(CLMatrixT<double>& m, const CLMatrixT<double>& rhs)
{
     
	size_t r = min(m.rows(), rhs.rows());
	size_t c = min(m.cols(), rhs.cols());
	for (size_t i = 0; i < r; ++i)
		lineSub_sse(&m[i][0], &rhs[i][0], (int)c, &m[i][0]);
	return m;
}
//sse逐点相乘取并取和(内积)
inline float lineDotMul_sse(const float* left, const float* right, int nCounts) {
     	
#if CLMAT_FLOAT_USEAVX > 0
	if (nCounts >= 64) {
      //大于64阶才有效率体现
		__m256 sum8 = _mm256_setzero_ps();
		for (int k = nCounts - 8; k >= 0; k -= 8)  // do every 8 elements 
			sum8 = _mm256_add_ps(sum8, _mm256_mul_ps(_mm256_loadu_ps(left + k), _mm256_loadu_ps(right + k)));
		sum8 = _mm256_hadd_ps(sum8, sum8);
		sum8 = _mm256_hadd_ps(sum8, sum8);
		float c = (sum8.m256_f32[0] + sum8.m256_f32[4]);
		for (int k = (nCounts % 8) - 1; k >= 0; --k) // handle the last n%4elements
			c += left[k] * right[k];
		return c;
	}
#endif
	float c = 0;
	if (nCounts >= 4) {
     
		__m128 sum = _mm_setzero_ps();  //Initialize
		for (int k = nCounts - 4; k >= 0; k -= 4)  // do every 4 elements 
			sum = _mm_add_ps(sum, _mm_mul_ps(_mm_loadu_ps(left + k), _mm_loadu_ps(right + k)));
		sum = _mm_hadd_ps(sum, sum);
		_mm_store_ss(&c, _mm_hadd_ps(sum, sum));
	}
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		c += left[k] * right[k];
	return c;
}
inline double lineDotMul_sse(const double* left, const double* right, int nCounts) {
     
	double c = 0;
	if (nCounts >= 4) {
     
		__m256d sum = _mm256_setzero_pd();  //Initialize
		for (int k = nCounts - 4; k >= 0; k -= 4)  // sum every 4 elements 
			sum = _mm256_add_pd(sum, _mm256_mul_pd(_mm256_loadu_pd(left + k), _mm256_loadu_pd(right + k)));
		sum = _mm256_hadd_pd(sum, sum);
		c = sum.m256d_f64[0] + sum.m256d_f64[2];
	}
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		c += left[k] * right[k];
	return c;
}

template<class T1, class T2, class T3>
CLMatrixT<T3>& _dotMul_sse(const CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto I = lhs.rows(), K = lhs.cols(), J = rhs.cols();
	CLMatrixT<double> _b, a = lhs;
	m.resize(I, J);
	::T(rhs, _b);
#if CLMAT_USE_CXX_PPL > 0
	auto total = I * J;
	if (total >= DOTMUL_RANK_LIMIT * DOTMUL_RANK_LIMIT) {
     
		auto tsi = total / DOTMUL_BLOCKS + 1;
		parallel_for<size_t>(0, tsi,
			[&J, &K, &m, &a, &_b, &total](size_t idt) {
     
				size_t idx = idt * DOTMUL_BLOCKS;
				size_t ide = min(idx + DOTMUL_BLOCKS, total);
				for (; idx < ide; ++idx) {
     
					size_t i = idx / J;
					size_t j = idx % J;
					m[i][j] = T3(lineDotMul_sse(&a[i][0], &_b[j][0], (int)K));
				}
			});
		return m;
	}
#endif
	for (size_t i = 0; i < I; ++i) {
     
		for (size_t j = 0; j < J; ++j) {
     
			m[i][j] = T3(lineDotMul_sse(&a[i][0], &_b[j][0], (int)K));
		}
	}
	return m;
}
template<class T2, class T3>
CLMatrixT<T3>& _dotMul_sse(const CLMatrixT<double>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto I = lhs.rows(), K = lhs.cols(), J = rhs.cols();
	m.resize(I, J);
	CLMatrixT<double> _b; ::T(rhs, _b);
#if CLMAT_USE_CXX_PPL > 0
	auto total = I * J;
	if (total >= DOTMUL_RANK_LIMIT * DOTMUL_RANK_LIMIT) {
     
		auto tsi = total / DOTMUL_BLOCKS + 1;
		parallel_for<size_t>(0, tsi,
			[&J, &K, &m, &lhs, &_b, &total](size_t idt) {
     
				size_t idx = idt * DOTMUL_BLOCKS;
				size_t ide = min(idx + DOTMUL_BLOCKS, total);
				for (; idx < ide; ++idx) {
     
					size_t i = idx / J;
					size_t j = idx % J;
					m[i][j] = T3(lineDotMul_sse(&lhs[i][0], &_b[j][0], (int)K));
				}
			});
		return m;
	}
#endif
	for (size_t i = 0; i < I; ++i) {
     
		for (size_t j = 0; j < J; ++j) {
     
			m[i][j] = T3(lineDotMul_sse(&lhs[i][0], &_b[j][0], (int)K));
		}
	}
	return m;
}
template<class T2, class T3>
CLMatrixT<T3>& _dotMul_sse(const CLMatrixT<float>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto I = lhs.rows(), K = lhs.cols(), J = rhs.cols();
	m.resize(I, J);
	CLMatrixT<float> _b; ::T(rhs, _b);
#if CLMAT_USE_CXX_PPL > 0
	auto total = I * J;	
	if (total >= DOTMUL_RANK_LIMIT * DOTMUL_RANK_LIMIT) {
     
		auto tsi = total / DOTMUL_BLOCKS + 1;
		parallel_for<size_t>(0, tsi,
			[&J, &K, &m, &lhs, &_b, &total](size_t idt) {
     
				size_t idx = idt * DOTMUL_BLOCKS;
				size_t ide = min(idx + DOTMUL_BLOCKS, total);
				for (; idx < ide;++idx) {
     
					size_t i = idx / J;
					size_t j = idx % J;
					m[i][j] = T3(lineDotMul_sse(&lhs[i][0], &_b[j][0], (int)K));
				}
		});
		return m;
	}
#endif
	for (size_t i = 0; i < I; ++i) {
     
		for (size_t j = 0; j < J; ++j) {
     
			m[i][j] = T3(lineDotMul_sse(&lhs[i][0], &_b[j][0], (int)K));
		}
	}
	return m;
}
//sse逐点相乘
inline void lineMul_sse(const float* left, const float* right, int nCounts, float* save) {
     
#if CLMAT_FLOAT_USEAVX > 0
	for (int k = nCounts - 8; k >= 0; k -= 8)  // do every 8 elements 
		_mm256_storeu_ps(save + k, _mm256_mul_ps(_mm256_loadu_ps(left + k), _mm256_loadu_ps(right + k)));
	for (int k = (nCounts % 8) - 4; k >= 0; k -= 4)  // do every 4 elements 
#else
	for (int k = nCounts - 4; k >= 0; k -= 4)  // do every 4 elements 
#endif
		_mm_storeu_ps(save + k, _mm_mul_ps(_mm_loadu_ps(left + k), _mm_loadu_ps(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] * right[k];
}
inline void lineMul_sse(const double* left, const double* right, int nCounts, double* save) {
     
	for (int k = nCounts - 4; k >= 0; k -= 4)  // sum every 4 elements 
		_mm256_storeu_pd(save + k, _mm256_mul_pd(_mm256_loadu_pd(left + k), _mm256_loadu_pd(right + k)));
	for (int k = (nCounts % 4) - 1; k >= 0; --k) // handle the last n%4elements
		save[k] = left[k] * right[k];
}
template<class T1, class T2, class T3>
CLMatrixT<T3>& _mul_sse(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	if (rhs.rows() == 1)
		for (size_t i = 0; i < r1; ++i)
			for (size_t j = 0; j < c1; ++j)
				m[i][j] = T3(lhs[i][j] * rhs[0][j]);
	else
		for (size_t i = 0; i < r1; ++i)
			for (size_t j = 0; j < c1; ++j)
				m[i][j] = T3(lhs[i][j] * rhs[i][j]);
	return m;
}
template<>inline CLMatrixT<float>& _mul_sse(const  CLMatrixT<float>& lhs, const  CLMatrixT<float>& rhs, CLMatrixT<float>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	if (rhs.rows() == 1)
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &rhs[0][0], (int)c1, &m[i][0]);
	else
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &rhs[i][0], (int)c1, &m[i][0]);
	return m;
}
template<>inline CLMatrixT<double>& _mul_sse(const  CLMatrixT<double>& lhs, const  CLMatrixT<double>& rhs, CLMatrixT<double>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	if (rhs.rows() == 1)
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &rhs[0][0], (int)c1, &m[i][0]);
	else
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &rhs[i][0], (int)c1, &m[i][0]);
	return m;
}
template<class T1, class T2, class T3>
CLMatrixT<T3>& _mul_T_sse(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	if (rhs.rows() == 1)
		for (size_t i = 0; i < r1; ++i)
			for (size_t j = 0; j < c1; ++j)
				m[i][j] = T3(lhs[i][j] * rhs[j][0]);
	else
		for (size_t i = 0; i < r1; ++i)
			for (size_t j = 0; j < c1; ++j)
				m[i][j] = T3(lhs[i][j] * rhs[j][i]);
	return m;
}
template<>inline CLMatrixT<float>& _mul_T_sse(const  CLMatrixT<float>& lhs, const  CLMatrixT<float>& rhs, CLMatrixT<float>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	CLMatrixT<float> b;
	::T(rhs, b);
	if (b.rows() == 1)
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &b[0][0], (int)c1, &m[i][0]);
	else
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &b[i][0], (int)c1, &m[i][0]);
	return m;
}
template<>inline CLMatrixT<double>& _mul_T_sse(const  CLMatrixT<double>& lhs, const  CLMatrixT<double>& rhs, CLMatrixT<double>& m) {
     
	auto r1 = lhs.rows(), c1 = lhs.cols();
	m.resize(r1, c1);
	CLMatrixT<double> b;
	::T(rhs, b);
	if (b.rows() == 1)
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &b[0][0], (int)c1, &m[i][0]);
	else
		for (size_t i = 0; i < r1; i++)
			lineMul_sse(&lhs[i][0], &b[i][0], (int)c1, &m[i][0]);
	return m;
}
inline CLMatrixT<float>& conv( //float 特化
	const CLMatrixT<float>& M, //卷积输入map
	const CLMatrixT<float>& K, //卷积核
	CLMatrixT<float>& F, //结果集feature map
	size_t _stepX = 1, //卷积核X移动步长
	size_t _stepY = 1, //卷积核Y移动步长
	size_t padding = 0,//输入map边缘填充宽度
	double paddingValue = 0.0//输入map边缘填充内填充的值（该值不一定是0，根据计算需要自由设置）
) {
     
	if (M.isEmpty() || K.isEmpty())
		return F.clear();
	if (padding >= min(K.rows(), K.cols()))
		return F.clear();
	int stepX = max(int(_stepX), 1);
	int stepY = max(int(_stepY), 1);
	int cc = ((int)M.cols() + 2 * (int)padding - (int)K.cols()) / stepX + 1;
	int rr = ((int)M.rows() + 2 * (int)padding - (int)K.rows()) / stepY + 1;
	rr = max(rr, 0);
	cc = max(0, cc);
	F.make(rr, cc, 0);
#if CLMAT_USE_CXX_PPL > 0
	auto total = rr * cc;  //PPL处理块
	if (total >= CONV_RANK_LIMIT * CONV_RANK_LIMIT) {
     
		auto tsi = total / CONV_BLOCKS + 1;
		parallel_for<int>(0, tsi, 
			[&](int idt) {
     
			int idx = idt * CONV_BLOCKS;
			int ide = min(idx + CONV_BLOCKS, total);
			for (; idx < ide; ++idx) {
     
				int r = idx / cc;
				int c = idx % cc;
				double t = 0;
				int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
				int kr = 0; int kc = 0;
				for (; i < 0; ++i, kc = 0, ++kr) // up padding
				{
     
					auto pk = &K[kr][0];
					for (; kc < int(K.cols()); ++kc)
						t += paddingValue * *pk++;
				}
				for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
				{
     
					int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
					auto pk = &K[kr][0];
					for (; j < 0; ++j) // left padding									
						t += paddingValue * *pk++;
					int top2 = min(sj, (int)M.cols());
					int nCounts = top2 - j;
					if (nCounts > 0) {
      // 采用SSE
						t += lineDotMul_sse(&M[i][j], pk, nCounts);
						j += nCounts;
						pk += nCounts;
					}
					for (; j < sj; ++j)  // right padding			
						t += paddingValue * *pk++;
				}
				for (; i < si; ++i, kc = 0, ++kr) // down padding
				{
     
					auto pk = &K[kr][0];
					for (; kc < int(K.cols()); ++kc)
						t += paddingValue * *pk++;
				}
				F[r][c] = float(t);
			}
			});
		return F;
	}
#endif
	for (int r = 0; r < rr; ++r) {
      //serial处理块	
		for (int c = 0; c < cc; ++c) {
     
			double t = 0;
			int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
			int kr = 0; int kc = 0;
			for (; i < 0; ++i, kc = 0, ++kr) // up padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
			{
     
				int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
				auto pk = &K[kr][0];
				for (; j < 0; ++j) // left padding									
					t += paddingValue * *pk++;
				int top2 = min(sj, (int)M.cols());
				int nCounts = top2 - j;
				if (nCounts > 0) {
      // 采用SSE
					t += lineDotMul_sse(&M[i][j], pk, nCounts);
					j += nCounts;
					pk += nCounts;
				}
				for (; j < sj; ++j)  // right padding			
					t += paddingValue * *pk++;
			}
			for (; i < si; ++i, kc = 0, ++kr) // down padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			F[r][c] = float(t);
		}
	};
	return F;
} //end func
inline CLMatrixT<double>& conv( //double 特化
	const CLMatrixT<double>& M, //卷积输入map
	const CLMatrixT<double>& K, //卷积核
	CLMatrixT<double>& F, //结果集feature map
	size_t _stepX = 1, //卷积核X移动步长
	size_t _stepY = 1, //卷积核Y移动步长
	size_t padding = 0,//输入map边缘填充宽度
	double paddingValue = 0.0//输入map边缘填充内填充的值（该值不一定是0，根据计算需要自由设置）
) {
     
	if (M.isEmpty() || K.isEmpty())
		return F.clear();
	if (padding >= min(K.rows(), K.cols()))
		return F.clear();
	int stepX = max(int(_stepX), 1);
	int stepY = max(int(_stepY), 1);
	int cc = ((int)M.cols() + 2 * (int)padding - (int)K.cols()) / stepX + 1;
	int rr = ((int)M.rows() + 2 * (int)padding - (int)K.rows()) / stepY + 1;
	rr = max(rr, 0);
	cc = max(0, cc);
	F.make(rr, cc, 0);
#if CLMAT_USE_CXX_PPL > 0
	auto total = rr * cc;  //PPL处理块
	if (total >= CONV_RANK_LIMIT * CONV_RANK_LIMIT) {
     
		auto tsi = total / CONV_BLOCKS + 1;
		parallel_for<int>(0, tsi,
			[&](int idt) {
     
				int idx = idt * CONV_BLOCKS;
				int ide = min(idx + CONV_BLOCKS, total);
				for (; idx < ide; ++idx) {
     
					int r = idx / cc;
					int c = idx % cc;
					double t = 0;
					int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
					int kr = 0; int kc = 0;
					for (; i < 0; ++i, kc = 0, ++kr) // up padding
					{
     
						auto pk = &K[kr][0];
						for (; kc < int(K.cols()); ++kc)
							t += paddingValue * *pk++;
					}
					for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
					{
     
						int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
						auto pk = &K[kr][0];
						for (; j < 0; ++j) // left padding									
							t += paddingValue * *pk++;
						int top2 = min(sj, (int)M.cols());
						int nCounts = top2 - j;
						if (nCounts > 0) {
      // 采用SSE
							t += lineDotMul_sse(&M[i][j], pk, nCounts);
							j += nCounts;
							pk += nCounts;
						}
						for (; j < sj; ++j)  // right padding			
							t += paddingValue * *pk++;
					}
					for (; i < si; ++i, kc = 0, ++kr) // down padding
					{
     
						auto pk = &K[kr][0];
						for (; kc < int(K.cols()); ++kc)
							t += paddingValue * *pk++;
					}
					F[r][c] = double(t);
				}
			});
		return F;
	}
#endif
	for (int r = 0; r < rr; ++r) {
      //serial处理块	
		for (int c = 0; c < cc; ++c) {
     
			double t = 0;
			int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
			int kr = 0; int kc = 0;
			for (; i < 0; ++i, kc = 0, ++kr) // up padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
			{
     
				int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
				auto pk = &K[kr][0];
				for (; j < 0; ++j) // left padding									
					t += paddingValue * *pk++;
				int top2 = min(sj, (int)M.cols());
				int nCounts = top2 - j;
				if (nCounts > 0) {
      // 采用SSE
					t += lineDotMul_sse(&M[i][j], pk, nCounts);
					j += nCounts;
					pk += nCounts;
				}
				for (; j < sj; ++j)  // right padding			
					t += paddingValue * *pk++;
			}
			for (; i < si; ++i, kc = 0, ++kr) // down padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			F[r][c] = double(t);
		}
	};
	return F;
} //end func

#endif //end sse

//矩阵的标准乘法(内积)
template<class T1, class T2, class T3>
CLMatrixT<T3>& dotMul(const CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto c = lhs.cols(), r = rhs.rows();
	if (c != r)
	{
     
		m.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" dotMul \", left obj cols(%d) != right obj rows(%d)!", (int)c, (int)r);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:dotMul");
	}
#if CLMAT_USE_SSE > 0
	if (matrixUseSSE && c >= matrixUseSSEMinRank) //经过测试矩阵横向宽度小于16将没有速度优势，故不再使用SSE
		return ::_dotMul_sse(lhs, rhs, m);
#endif
	r = lhs.rows(), c = rhs.cols();
	m.resize(r, c);
	size_t K = lhs.cols();
#if CLMAT_USE_CXX_PPL > 0  //PPL 代码块
	auto total = r * c;
	if (total >= DOTMUL_RANK_LIMIT * DOTMUL_RANK_LIMIT) {
     
		auto tsi = total / DOTMUL_BLOCKS + 1;
		parallel_for<size_t>(0, tsi,
			[&c, &K, &m, &lhs, &rhs, &total](size_t idt) {
     
				size_t idx = idt * DOTMUL_BLOCKS;
				size_t ide = min(idx + DOTMUL_BLOCKS, total);
				for (; idx < ide; ++idx) {
     
					size_t i = idx / c;
					size_t j = idx % c;
					T1 sum = 0;
					for (size_t k = 0; k < K; ++k) {
     
						sum += lhs[i][k] * rhs[k][j];
					}
					m[i][j] = T3(sum);
				}
			});
		return m;
	}
#endif
	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			T1 sum = 0;
			for (size_t k = 0; k < K; ++k) {
     
				sum += lhs[i][k] * rhs[k][j];
			}
			m[i][j] = T3(sum);
		}
	}
	return m;
}
//矩阵逐点相乘。当左右操作数的列数应该对应相同，且右操作数行必须为1或大于左操作数的行。
template<class T1, class T2, class T3>
CLMatrixT<T3>& mul(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto c1 = lhs.cols(), r1 = lhs.rows();
	auto c2 = rhs.cols(), r2 = rhs.rows();
	if (c2 == c1) {
     
		if (r2 == 1) {
     
#if CLMAT_USE_SSE > 0
			if (matrixUseSSE /*&& c2 >= matrixUseSSEMinRank*/)
				return ::_mul_sse(lhs, rhs, m);
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[0][j]);
			return m;
		}
		else if (r2 >= r1) {
     
#if CLMAT_USE_SSE > 0
			if (matrixUseSSE /*&& c2 >= matrixUseSSEMinRank*/)
				return ::_mul_sse(lhs, rhs, m);
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[i][j]);
			return m;
		}
		m.clear();
		// never arrive here.
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul \", cols match, but right obj rows(%d) != 1 and < left obj rows(%d)!", (int)r2, (int)r1);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
	else {
     
		m.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul \", cols ( %d != %d ) it is not match!", (int)c1, (int)c2);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
}
//矩阵逐点相乘,右操作数是按其转置来处理逐点相乘的。当右操作数的列数对应的左操作数行相同，且右操作数的列必须为1或大于左操作数的行。
template<class T1, class T2, class T3>
CLMatrixT<T3>& mul_T(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto c1 = lhs.cols(), r1 = lhs.rows();
	auto c2 = rhs.rows(), r2 = rhs.cols();
	if (c2 == c1) {
     
		if (r2 == 1) {
     
#if CLMAT_USE_SSE > 0
			if (matrixUseSSE && c2 >= matrixUseSSEMinRank)
				return ::_mul_T_sse(lhs, rhs, m);
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[j][0]);
			return m;
		}
		else if (r2 >= r1) {
     
#if CLMAT_USE_SSE > 0
			if (matrixUseSSE && c2 >= matrixUseSSEMinRank)
				return ::_mul_T_sse(lhs, rhs, m);
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[j][i]);
			return m;
		}
		m.clear();
		// never arrive here.
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_T \", cols match, but right obj cols(%d) != 1 and < left obj rows(%d)!", (int)r2, (int)r1);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
	else {
     
		m.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_T \", left cols(%d) !=  right rows(%d) , it is not match!", (int)c1, (int)c2);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
}
//矩阵按列逐点相乘。当左右操作数的行数应该对应相同，且右操作数列必须为1或大于左操作数的列数。
template<class T1, class T2, class T3>
CLMatrixT<T3>& mul_V(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto c1 = lhs.cols(), r1 = lhs.rows();
	auto c2 = rhs.cols(), r2 = rhs.rows();
	if (r2 == r1) {
     
		if (c2 == 1) {
     
#if CLMAT_USE_SSE > 0
			//if (matrixUseSSE && r2 >= matrixUseSSEMinRank)
			//	return ::_mul_T_sse(::T(lhs, CLMatrixT()), rhs, m).makeT();
			// 此位置不能采用加速
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[i][0]);
			return m;
		}
		else if (c2 >= c1) {
     
#if CLMAT_USE_SSE > 0
			if (matrixUseSSE /*&& c2 >= matrixUseSSEMinRank*/)
				return ::_mul_sse(lhs, rhs, m);
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[i][j]);
			return m;
		}
		m.clear();
		// never arrive here.
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_V \", rows match, but right obj cols(%d) != 1 and < left obj cols(%d)!", (int)c2, (int)c1);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
	else {
     
		m.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_V \", rows ( %d != %d ) it is not match!", (int)r1, (int)r2);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
}
//矩阵按列逐点相乘,右操作数是按其转置来处理逐点相乘的。当右操作数的行数对应的左操作数列相同，且右操作数的行必须为1或大于左操作数的列。
template<class T1, class T2, class T3>
CLMatrixT<T3>& mul_VT(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs, CLMatrixT<T3>& m)
{
     
	auto c1 = lhs.cols(), r1 = lhs.rows();
	auto r2 = rhs.cols(), c2 = rhs.rows();
	if (r2 == r1) {
     
		if (c2 == 1) {
     
#if CLMAT_USE_SSE > 0
			//if (matrixUseSSE && r1 >= matrixUseSSEMinRank)
			//	return  ::_mul_sse(::T(lhs, CLMatrixT()), rhs, m).makeT();
			// 此位置不能采用加速
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[0][i]);
			return m;
		}
		else if (c2 >= c1) {
     
#if CLMAT_USE_SSE > 0
			//if (matrixUseSSE && r1 >= matrixUseSSEMinRank)
			//	return  ::_mul_sse(::T(lhs, CLMatrixT()), rhs, m).makeT();
#endif
			m.resize(r1, c1);
			for (size_t i = 0; i < r1; ++i)
				for (size_t j = 0; j < c1; ++j)
					m[i][j] = T3(lhs[i][j] * rhs[j][i]);
			return m;
		}
		m.clear();
		// never arrive here.
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_VT \", rows and cols is match, but right obj rows(%d) != 1 and < left obj cols(%d)!", (int)c2, (int)c1);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
	else {
     
		m.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" mul_VT \", left rows(%d) !=  right cols(%d) , it is not match!", (int)r1, (int)r2);
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:operator*");
	}
}
template<class T1, class T2>
CLMatrixT<T1> operator*(const CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs)
{
     
	return ::dotMul(lhs, rhs, (CLMatrixT<T1>&)CLMatrixT<T1>());
}
template<class T1, class T2>
CLMatrixT<T1> operator*(const  CLMatrixT<T1>& lhs, T2 v)
{
     
	auto m = lhs;
	m *= T1(v);
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator*(T2 v, const  CLMatrixT<T1>& lhs)
{
     
	auto m = lhs;
	m *= T1(v);
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator/(const  CLMatrixT<T1>& lhs, const  CLMatrixT<T2>& rhs)
{
     
	CLMatrixT<T2> tmp;
	inv(rhs, tmp);
	if (tmp.isEmpty())
		return tmp;
	return lhs * tmp;
}
template<class T1, class T2>
CLMatrixT<T1> operator/(const  CLMatrixT<T1>& lhs, T2 v)
{
     
	auto m = lhs;
	m /= v;
	return m;
}
template<class T1, class T2>
CLMatrixT<T1> operator/(T2 v, const  CLMatrixT<T1>& lhs)
{
     
	return lhs.pow(-1.0) * v;
}
// 计算方阵 M 的 LU 分解,使得 M = LU
// 其中L为对角线元素全为1的下三角阵，U为对角元素依赖M的上三角阵
template<class T1, class T2, class T3>bool LU(const CLMatrixT<T1>& A, CLMatrixT<T2>& L, CLMatrixT<T3>& U)
{
     
	if (A.isEmpty())
	{
     
		L.clear(); U.clear();
		char err[256];
		sprintf_s(err, "Error: CLMatrixT method \" LUP \", matix obj is empty matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:LUP");
	}
	else if (!A.isSquare()) {
     
		L.clear(); U.clear();
		char err[BUFSIZE];
		sprintf_s(err, "Error: CLMatrixT method \" LUP \", matix obj is not a square matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:LUP");
	}
	auto M = A;
	if (!LUP_Descomposition(M, L, U, CLMatrixT<size_t>())) {
     
		cout << endl << "[Runtime error]: Matrix is singular, unable to calculate inverse!" << endl;
		return false;
	}
	return true;
}
//LUP分解
template<class T1, class T2, class T3>bool LUP_Descomposition(CLMatrixT<T1>& A, CLMatrixT<T2>& L, CLMatrixT<T3>& U, CLMatrixT<size_t>& PLine)
{
     
	size_t N = A.rows();
	L.resize(N, N);
	U.resize(N, N);
	PLine.resize(1, N);
	auto& P = PLine[0];
	size_t row = 0;
	for (size_t i = 0; i < N; ++i)
	{
     
		P[i] = i;
	}
	for (size_t i = 0; i < N - 1; ++i)
	{
     
		T1 p = 0;
		for (size_t j = i; j < N; ++j)
		{
     
			if (abs(A[j][i]) > p)
			{
     
				p = abs(A[j][i]);
				row = j;
			}
		}
		if (0 == p)
		{
     
			//cout << endl << "矩阵奇异，无法计算逆" << endl;
			return false;
		}

		//交换P[i]和P[row]
		size_t tmp = P[i];
		P[i] = P[row];
		P[row] = tmp;

		T1 tmp2 = 0;
		for (size_t j = 0; j < N; ++j)
		{
     
			//交换A[i][j]和 A[row][j]
			tmp2 = A[i][j];
			A[i][j] = A[row][j];
			A[row][j] = tmp2;
		}

		//以下同LU分解
		T1 u = A[i][i], l = 0;
		for (size_t j = i + 1; j < N; ++j)
		{
     
			l = A[j][i] / u;
			A[j][i] = l;
			for (size_t k = i + 1; k < N; ++k)
			{
     
				A[j][k] = A[j][k] - A[i][k] * l;
			}
		}

	}

	//构造L和U
	for (size_t i = 0; i < N; ++i)
	{
     
		for (size_t j = 0; j <= i; ++j)
		{
     
			if (i != j)
			{
     
				L[i][j] = A[i][j];
			}
			else
			{
     
				L[i][j] = 1;
			}
		}
		for (size_t k = i; k < N; ++k)
		{
     
			U[i][k] = A[i][k];
		}
	}
	return true;
}
//LUP求解方程
template<class T1, class T2, class T3>
void LUP_Solve(size_t N, CLMatrixT<T1>& X, CLMatrixT<T1>& Y, const CLMatrixT<T2>& L, const CLMatrixT<T3>& U, const CLMatrixT<size_t>& PLine, const CLMatrixT<T1>& B)
{
     
	auto& P = PLine[0];
	auto& b = B[0];
	X.resize(1, N);
	Y.resize(1, N);
	auto& x = X[0];
	auto& y = Y[0];
	//正向替换
	for (size_t i = 0; i < N; ++i)
	{
     
		y[i] = b[P[i]];
		for (size_t j = 0; j < i; ++j)
		{
     
			y[i] = y[i] - L[i][j] * y[j];
		}
	}
	//反向替换
	for (int i = N - 1; i >= 0; i--)
	{
     
		x[i] = y[i];
		for (int j = N - 1; j > i; j--)
		{
     
			x[i] = x[i] - U[i][j] * x[j];
		}
		x[i] /= U[i][i];
	}
}
//LUP分解求逆
template<class T1, class T2> CLMatrixT<T2>& LUP_Inverse(const CLMatrixT<T1>& A, CLMatrixT<T2>& ret)
{
     
	if (A.isEmpty())
	{
     
		ret.clear();
		char err[BUFSIZE];
		sprintf_s(err, "Error: CLMatrixT method \" inv \", matix obj is empty matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:inv");
	}
	else if (!A.isSquare()) {
     
		ret.clear();
		char err[BUFSIZE];
		sprintf_s(err, "Error: CLMatrixT method \" inv \", matix obj is not a square matrix!");
		_CLMatrixT_Runtime_Error_Box(err);
		throw std::runtime_error("CLMatrixT Runtime Error:inv");
	}

	size_t N = A.cols();

	CLMatrixT<float> A_mirror(N, N);
	CLMatrixT<float> inv_A(N, N);//最终的逆矩阵（还需要转置）
	CLMatrixT<float> inv_A_each(1, N);//矩阵逆的各列
	CLMatrixT<float> B(1, N);//b阵为B阵的列矩阵分量
	CLMatrixT<float> Y(1, N);//b阵为B阵的列矩阵分量
	CLMatrixT<float> L(N, N);
	CLMatrixT<float> U(N, N);

	//CLMatrixT A_mirror(N, N);
	//CLMatrixT inv_A(N, N);//最终的逆矩阵（还需要转置）
	//CLMatrixT inv_A_each(1, N);//矩阵逆的各列
	//CLMatrixT B(1, N);//b阵为B阵的列矩阵分量
	//CLMatrixT Y(1, N);//b阵为B阵的列矩阵分量
	//CLMatrixT L(N, N);
	//CLMatrixT U(N, N);

	CLMatrixT<size_t> P(1, N);
	for (size_t i = 0; i < N; ++i)
	{
     
		//构造单位阵的每一列
		for (size_t j = 0; j < N; ++j)B[0][j] = 0;
		B[0][i] = 1;
		A_mirror = A;
		if (!LUP_Descomposition(A_mirror, L, U, P)) {
     
			//奇异矩阵返回矩阵
			//cout << endl << "[Runtime error]: Matrix is singular, unable to calculate inverse!" << endl;
			return ret.clear();
		}
		LUP_Solve(N, inv_A_each, Y, L, U, P, B);
		inv_A.setRow(i, inv_A_each[0]);
	}
	return ::T(inv_A, ret);
}
template<class T2> CLMatrixT<T2>& LUP_Inverse(const CLMatrixT<double>& A, CLMatrixT<T2>& ret) {
     
	return ::LUP_Inverse<float, T2>(CLMatrixT<float>(A), ret);
}
//将一个矩阵变换到对角线矩阵，同一行列的值都加到主对角上
template<class T1, class T2>CLMatrixT<T2>& diag(const CLMatrixT<T1>& m, CLMatrixT<T2>& ret) {
     
	auto r = m.rows(), c = m.cols();
	if (r == 0 || c == 0)
		return ret.clear();
	auto si = max(r, c);
	ret.makeSquare(si, 0);
	for (size_t i = 0; i < r; ++i)
	{
     
		for (size_t j = 0; j < c; ++j)
		{
     
			if (j >= i)
				ret[j][j] += m[i][j];
			else
				ret[i][i] += m[i][j];
		}
	}
	return ret;
}

template<class T1, class T2, class T3> CLMatrixT<T3>& conv(
	const CLMatrixT<T1>& M, //卷积输入map
	const CLMatrixT<T2>& K, //卷积核
	CLMatrixT<T3>& F, //结果集feature map
	size_t _stepX = 1, //卷积核X移动步长
	size_t _stepY = 1, //卷积核Y移动步长
	size_t padding = 0,//输入map边缘填充宽度
	double paddingValue = 0.0//输入map边缘填充内填充的值（该值不一定是0，根据计算需要自由设置）
) {
     
	if (M.isEmpty() || K.isEmpty())
		return F.clear();
	if (padding >= min(K.rows(), K.cols()))
		return F.clear();
	int stepX = max(int(_stepX), 1);
	int stepY = max(int(_stepY), 1);
	int cc = ((int)M.cols() + 2 * (int)padding - (int)K.cols()) / stepX + 1;
	int rr = ((int)M.rows() + 2 * (int)padding - (int)K.rows()) / stepY + 1;
	rr = max(rr, 0);
	cc = max(0, cc);
	F.make(rr, cc, 0);
#if CLMAT_USE_CXX_PPL > 0
	auto total = rr * cc;  //PPL处理块
	if (total >= CONV_RANK_LIMIT * CONV_RANK_LIMIT) {
     
		auto tsi = total / CONV_BLOCKS + 1;
		parallel_for<int>(0, tsi, [&](int idt) {
     
			int idx = idt * CONV_BLOCKS;
			int ide = min(idx + CONV_BLOCKS, total);
			for (; idx < ide; ++idx) {
     
				int r = idx / cc;
				int c = idx % cc;
				double t = 0;
				int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
				int kr = 0; int kc = 0;
				for (; i < 0; ++i, kc = 0, ++kr) // up padding
				{
     
					auto pk = &K[kr][0];
					for (; kc < int(K.cols()); ++kc)
						t += paddingValue * *pk++;
				}
				for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
				{
     
					int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
					auto pk = &K[kr][0];
					for (; j < 0; ++j) // left padding									
						t += paddingValue * *pk++;
					for (int top2 = min(sj, (int)M.cols()); j < top2; ++j)
						t += M[i][j] * *pk++;
					for (; j < sj; ++j)  // right padding			
						t += paddingValue * *pk++;
				}
				for (; i < si; ++i, kc = 0, ++kr) // down padding
				{
     
					auto pk = &K[kr][0];
					for (; kc < int(K.cols()); ++kc)
						t += paddingValue * *pk++;
				}
				F[r][c] = T3(t);
			}
			}); 
		return F;
	}
#endif
	for (int r = 0; r < rr; ++r) {
      //serial处理块	
		for (int c = 0; c < cc; ++c) {
     
			double t = 0;
			int i = 0 - int(padding) + int(r * stepY), si = i + int(K.rows());
			int kr = 0; int kc = 0;
			for (; i < 0; ++i, kc = 0, ++kr) // up padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			for (int top = min(si, (int)M.rows()); i < top; ++i, kc = 0, ++kr)
			{
     
				int j = 0 - int(padding) + int(c * stepX), sj = j + int(K.cols());
				auto pk = &K[kr][0];
				for (; j < 0; ++j) // left padding									
					t += paddingValue * *pk++;
				for (int top2 = min(sj, (int)M.cols()); j < top2; ++j)
					t += M[i][j] * *pk++;
				for (; j < sj; ++j)  // right padding			
					t += paddingValue * *pk++;
			}
			for (; i < si; ++i, kc = 0, ++kr) // down padding
			{
     
				auto pk = &K[kr][0];
				for (; kc < int(K.cols()); ++kc)
					t += paddingValue * *pk++;
			}
			F[r][c] = T3(t);
		}
	}; 
	return F;
} //end func

#define CLMATRIX_CALLBACK_PARAM float& v, size_t r, size_t c //传参类型:v元素项引用，r元素行标，c元素列标
typedef CLMatrixT<float> CLMatrix;//float型矩阵类
#define CLMATRIXD_CALLBACK_PARAM double& v, size_t r, size_t c
typedef CLMatrixT<double> CLMatrixD;//double型矩阵类
#define CLMATRIXF_CALLBACK_PARAM float& v, size_t r, size_t c
typedef CLMatrixT<float> CLMatrixF;//float型矩阵类
#define CLMATRIXS_CALLBACK_PARAM short& v, size_t r, size_t c
typedef CLMatrixT<short> CLMatrixS;//short型矩阵类
#define CLMATRIXI_CALLBACK_PARAM int& v, size_t r, size_t c
typedef CLMatrixT<int> CLMatrixI;//int型矩阵类
#define CLMATRIXLL_CALLBACK_PARAM long long& v, size_t r, size_t c
typedef CLMatrixT<long long> CLMatrixLL;//long long型矩阵类
#define CLMATRIXL_CALLBACK_PARAM long& v, size_t r, size_t c
typedef CLMatrixT<long> CLMatrixL;//long型矩阵类

//测试检查本机SSE参数的最佳值，返回值用于CLMatrix::setUseSSEMinRank()的参数
inline size_t matrixSSEParamFitValue() {
     
	auto MakeXF = [](CLMATRIXF_CALLBACK_PARAM) {
      v = 1; };
	auto MakeXD = [](CLMATRIXD_CALLBACK_PARAM) {
      v = 1; };
	auto MakeXI = [](CLMATRIXI_CALLBACK_PARAM) {
      v = 1; };
	size_t base = 1, times = 1000;
	auto bkset = CLMatrix::setUseSSE(true);
	auto bksi = CLMatrix::setUseSSEMinRank(0);
	size_t mk1 = 0, mk2 = 0, mk3 = 0;
	for (size_t i = 0; i < 20; i++)
	{
     
		base += 1;
		CLMatrixF a(base, MakeXF), b(base, MakeXF);
		CLMatrixD c(base, MakeXD), d(base, MakeXD);
		CLMatrixI e(base, MakeXI), f(base, MakeXI);
		CLMatrix::setUseSSE(true);
		auto t0 = clock();
		for (size_t j = 0; j < times; j++)a* b;
		auto t1 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)c* d;
		auto t2 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)e* f;
		auto t5 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		CLMatrix::setUseSSE(false);
		for (size_t j = 0; j < times; j++)a* b;
		auto t3 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)c* d;
		auto t4 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)e* f;
		auto t6 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		if (mk1 == 0 && t1 < t3)mk1 = i + 2;
		if (mk2 == 0 && t2 < t4)mk2 = i + 2;
		if (mk3 == 0 && t5 < t6)mk3 = i + 2;
		if (mk1 && mk2 && mk3)
			break;
	}
	CLMatrix::setUseSSE(bkset);
	CLMatrix::setUseSSEMinRank(bksi);
	size_t rt = (2 * mk2 + 7 * mk1 + 1 * mk3) / 10;
	return rt;
}
// 做本地效率测试,并输出结果
inline void matrixLocalTest() {
     
#define AXB a.conv(b)
#define CXD c.conv(d)
#define EXF e.conv(f)
//#define AXB a* b
//#define CXD c* d
//#define EXF e* f
//#define AXB a/ b
//#define CXD c/ d
//#define EXF e/ f
//#define AXB a.mul_V(b)
//#define CXD c.mul_V(d)
//#define EXF e.mul_V(f)
//#define AXB a.mul_T(b)
//#define CXD c.mul_T(d)
//#define EXF e.mul_T(f)
//#define AXB a.mul(b)
//#define CXD c.mul(d)
//#define EXF e.mul(f)
//#define AXB (a+b)
//#define CXD (c-d)
//#define EXF (e+f)
	auto bku = CLMatrix::isUseSSE();
	cout << "\n\n测试本机不同大小矩阵的类型运行效率----------------------------------";
	srand((unsigned int)time(0));
	auto MakeXF = [](CLMATRIXF_CALLBACK_PARAM) {
      v = rand() % 100 * 0.01f; };
	auto MakeXD = [](CLMATRIXD_CALLBACK_PARAM) {
      v = rand() % 100 * 0.01; };
	auto MakeXI = [](CLMATRIXI_CALLBACK_PARAM) {
      v = rand() % 10; };
	size_t base = 1;
	size_t base2 = 1;
	size_t times = 10000000;
	cout << "\n\n指数级递增测试";
	for (size_t i = 0; base <= 512; i++)
	{
     
		base *= 2; times /= 4;
		times = max(1, times);
		//base2 = base;//卷积测试时候注释
		CLMatrixF a(base, MakeXF), b(base2, MakeXF);
		CLMatrixD c(base, MakeXD), d(base2, MakeXD);
		CLMatrixI e(base, MakeXI), f(base2, MakeXI);
		base2 = min(base/4, 64);
		//base2 = base2+2;
		CLMatrix::setUseSSE(true);
		auto t0 = clock();
		for (size_t j = 0; j < times; j++)AXB;
		auto t1 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)CXD;
		auto t2 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)EXF;
		auto t5 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		CLMatrix::setUseSSE(false);
		for (size_t j = 0; j < times; j++)AXB;
		auto t3 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)CXD;
		auto t4 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)EXF;
		auto t6 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		printf_s("\n%zd:%zd rank=%zd, f=%.3fs %s uf=%.3fs (%+.2f%%), d=%.3fs %s ud=%.3fs (%+.2f%%), i=%.3fs %s ui=%.3fs (%+.2f%%)",
			i + 1, times, base, t1, (t1 < t3 ? "快<" : ">"), t3, (t1 - t3) / t3 * 100,
			t2, (t2 < t4 ? "快<" : ">"), t4, (t2 - t4) / t4 * 100,
			t5, (t5 < t6 ? "快<" : ">"), t6, (t5 - t6) / t6 * 100);
	}
	cout << endl;
	CLMatrixF M1, M3;
	CLMatrixD M2, M4;
	CLMatrixI M5, M6;
	int open = 1;
	base = 1, base2 = 1; times = 1000000;
	cout << "\n线性递增测试";
	for (size_t i = 0; i < 31; i++)
	{
     
		base += 1; times = times * 4 / 5;
		//base2 = base;//卷积测试时候注释
		CLMatrixF a(base, MakeXF), b(base2, MakeXF);
		CLMatrixD c(base, MakeXD), d(base2, MakeXD);
		CLMatrixI e(base, MakeXI), f(base2, MakeXI);
		base2 = min(base / 2, 7);
		CLMatrix::setUseSSE(true);
		auto t0 = clock();
		for (size_t j = 0; j < times; j++)AXB;
		auto t1 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)CXD;
		auto t2 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)EXF;
		auto t5 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		CLMatrix::setUseSSE(false);
		for (size_t j = 0; j < times; j++)AXB;
		auto t3 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)CXD;
		auto t4 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		for (size_t j = 0; j < times; j++)EXF;
		auto t6 = double(clock() - t0) / CLOCKS_PER_SEC; t0 = clock();
		printf_s("\n%zd:%zd rank=%zd, f=%.3fs %s uf=%.3fs (%+.2f%%), d=%.3fs %s ud=%.3fs (%+.2f%%), i=%.3fs %s ui=%.3fs (%+.2f%%)",
			i + 1, times, base, t1, (t1 < t3 ? "快<" : ">"), t3, (t1 - t3) / t3 * 100,
			t2, (t2 < t4 ? "快<" : ">"), t4, (t2 - t4) / t4 * 100,
			t5, (t5 < t6 ? "快<" : ">"), t6, (t5 - t6) / t6 * 100);
		if (base > 8 && open) {
     
			open = 0;
			CLMatrix::setUseSSE(false);
			M1 = AXB;
			M2 = CXD;
			M5 = EXF;
			CLMatrix::setUseSSE(true);
			M3 = AXB;
			M4 = CXD;
			M6 = EXF;
		}
	}
	cout << endl;
	if (M1 != M3)
		M1.print(_T(" a * b no use")), M3.print(_T(" a * b use")), (M1 - M3).print(_T(" delta a b use"));
	if (M2 != M4)
		M2.print(_T(" c * d no use")), M4.print(_T(" c * d use")), (M2 - M4).print(_T(" delta c d use"));
	if (M5 != M6)
		M5.print(_T(" e * f no use")), M6.print(_T(" e * f use")), (M5 - M6).print(_T(" delta e f use"));
	cout << "\n当前矩阵的加速优化宽度最小宽度" << matrixUseSSEMinRank << endl << endl;
	CLMatrix::setUseSSE(bku);//还原
}

#endif