每日一题 | day24（年终奖 | 迷宫问题）

选择题

1、将N条长度均为M的有序链表进行合并，合并以后的链表也保持有序，时间复杂度为()?
A O(N * M * logN)
B O(N*M)
C O(N)
D O(M)

正确答案 A：在每一个链表中取出第一个值，然后把它们放在一个大小为N的数组里，然后把这个数组当成heap建成小(大)根堆。此步骤的时间复杂度为O(N)。取出堆中的最小值(也是数组的第一个值), 然后把该最小值所处的链表的下一个值放在数组的第一个位置，然后进行调整。如果链表中有一个已经为空（元素已经都被取出），则改变heap的大小。此步骤的时间复杂度为O(lg N)。不断的重复步骤二，直到所有的链表都为空。建堆只建一次，复杂度为O(N)；调整堆MN-1次（构建的时候抽走了根结点，剩下的数目是MN-1个数），复杂度为(MN-1)*O(lg N)。复杂度是O(N)+(MN-1)*O(lg N)，所以复杂度为O(MN *lg N)

2、n！后面有多少个0,6！=12345*6=720.720后面有1个0，n=10000，求n！
A 2498
B 2499
C 2450
D 2451
正确答案 B：一个数 n 的阶乘末尾有多少个 0 取决于从 1 到 n 的各个数的因子中 2 和 5 的个数, 而 2 的个数是远远多余 5 的个数的, 因此取决于5 的个数。现在问题的关键是如何求解因子5的个数。思路一，记录每个数的因子5的个数然后相加，但是这样很可能会超时。思路二，用 n 不断除以 5, 直到结果为 0, 然后把中间得到的结果累加。理由：不断除以 5, 是因为每间隔 5 个数有一个数可以被 5 整除, 然后在这些可被 5 整除的数中, 每间隔 5 个数又有一个可以被 25 整除, 故要再除一次, … 直到结果为 0, 表示没有能继续被 5 整除的数了。例如25的阶乘包含5的因子有5、10、15、20、25。而25中又可以分解成5*5。所以一共有6个0。

#include 
using namespace std;

int main()
{
     
	int n;
	cin >> n;
	int sum = 0;
	while (n)
	{
     
		sum += n /= 5;
	}
	cout << sum << endl;
	return 0;
}

3、下列选项中，不可能是快速排序第2趟排序结果的是 （）
A 2,3,5,4,6,7,9
B 2,7,5,6,4,3,9
C 3,2,5,4,7,6,9
D 4,2,3,5,7,6,9

正确答案 C：快排是每排一次都能至少确认一个数的位置。当第一趟元素确认的位置为最左或最右时，第二趟排序只能确认一个位置。当第一趟元素确认位置不是最左或最右时，第二趟能确认2个位置。最终排序结果为：{2,3,4,5,6,7,9}。D选项中只有9是确认的位置，所以不可能是第二趟排序

编程题

题目1：

题解思路：如下图所示

第一个点和最后一个点都是必须经过的，能走到最后的那个礼物，也就是上面或者左边的那个点才能走到。那就判断这两个点谁目前拿的礼物的价值大，谁大谁就加上最后一个礼物。而两个点也要向上看，看左边的点大还是右边的点大，谁大就加上谁。

这种方法修改了board里的礼物价值，且只能递归解决。效率有被限制，这里根据类似的思想，使用动态规划来解决效率会更高些。我们可以再定义一个矩阵allPrice。该矩阵就是存储目前最大礼物的价值。

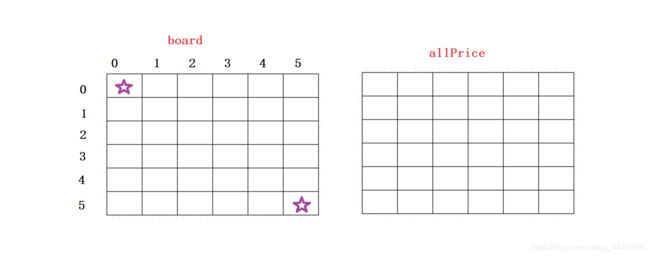
应为第一个礼物肯定要拿，我们就将allPrice第一个元素置为第一个礼物的价值，然后依次遍历两个矩阵。当属于第一行时，礼物只能由左边相加得到；当属于第一列时，礼物价格只能由上面来得到。其他元素都是可以从上边或者左边得到。判断上边和左边礼物的价值，谁大就加上当前位置的礼物，作为目前的最大礼物价格

示例如下：（可以配合动归代码一起看）

代码1：动归

//动态规划
class Bonus {
     
public:
    int getMost(vector<vector<int> > board) 
    {
     
        int row = board.size();
        int col = board[0].size();
        
        vector<vector<int>> allPrice(row, vector<int>(col, 0));
        allPrice[0][0] = board[0][0];
        
        for (int i = 0; i < row; ++i)
        {
     
            for (int j = 0; j < col; ++j)
            {
     
                if (i == 0 && j == 0)
                    continue;
                if (i == 0) //第一行，只能往右走
                    allPrice[i][j] = allPrice[i][j-1] + board[i][j];
                else if (j == 0)//在第一列，只能往下走
                    allPrice[i][j] = allPrice[i-1][j] + board[i][j];
                else
                    allPrice[i][j] = max(allPrice[i][j-1], allPrice[i-1][j]) + board[i][j];
            }
        }
        return allPrice[row-1][col-1];
    }
};

代码2：递归

class Bonus {
     
public:
	int maxGifts(vector<vector<int> > board, int i, int j)
	{
     
		if (i == 0 && j == 0)
			return board[0][0];
		if (i == 0)
			return maxGifts(board, i, j - 1) + board[i][j];
		if (j == 0)
			return maxGifts(board, i - 1, j) + board[i][j];
		return max(maxGifts(board, i, j - 1), maxGifts(board, i - 1, j)) + board[i][j];
	}
	int getMost(vector<vector<int> > board) 
	{
     
		return maxGifts(board, 5, 5);
	}
};

题目2：

解题思路：这道题要求我们找出走出迷宫的最短路径，这示例中有两条路可以走，都是最短路径只有一条。也就是红色的路线。因为我们是上帝视角，我们一下就可以看出路径有哪些，但是计算机并不是，计算机只能看到当前的值。所以就必须遍历每条路径，当路径可走时就往下走，走不了时就必须原路返回到下一个可走的路。所以这道题也就用到了回溯算法。

我们可以记录每条可以走到终点的路线，然后再判断路线经过的点数，最短路径就为经过点数最少的可行路径。如果没达到终点就继续走，可以向四个方向走，走时必须要考虑越界和墙的问题，例如向右走时遇到墙或者是已经走到边了都不能再向右走了。最后如果该路径四个方向都走不通，则表示该路径不能达到终点，则回溯。代码清晰，注释明了

代码：

#include 
#include 
using namespace std;

int ROW, COL;
vector<vector<int>> maze;//迷宫
vector<vector<int>> path;//路径
vector<vector<int>> shortPath;//最短路径

void MazeTrack(int i, int j)
{
     
    maze[i][j] = 1;//代表该点(i,j)已经走过
    path.push_back({
     i, j});//将该点保存在路径上
    
    //判断是否到达重点
    if (i == ROW-1 && j == COL-1)
    {
     
        //判断该路径是否为最短路径
        //如果这是第一个能到达终点的路径，则为最短路径
        //如果不是第一个到达重点的路径，则需要与之前路径相比谁的路径更短
        if (shortPath.empty() || path.size() < shortPath.size())
            shortPath = path;
    }
    //没有达到终点，则向四个方向走
    //向下走,没走到底并且当下一个位置不是墙就可以走
    if (i+1<ROW && maze[i+1][j] == 0)
        MazeTrack(i+1, j);
    //向上走,没走到顶并且当下一个位置不是墙就可以走
    if (i-1>=0 && maze[i-1][j] == 0)
        MazeTrack(i-1, j);
    //向右走,没走到边并且当下一个位置不是墙就可以走
    if (j+1<COL && maze[i][j+1] == 0)
        MazeTrack(i, j+1);
    //向左走,没走到边并且当下一个位置不是墙就可以走
    if (j-1>=0 && maze[i][j-1] == 0)
        MazeTrack(i, j-1);
    
    //四个方向都走不通，则回溯，往后退一步。
    maze[i][j] = 0;
    path.pop_back();
}

int main()
{
     
    
    while (cin >> ROW >> COL)
    {
     
        maze = vector<vector<int>>(ROW, vector<int>(COL, 0));
        //清除全局变量
        path.clear();
        shortPath.clear();
        //初始化迷宫
        for (int i = 0; i < ROW; ++i)
        {
     
            for (int j = 0; j < COL; ++j)
            {
     
                cin >> maze[i][j];
            }
        }
        MazeTrack(0, 0);//起始位置
        for (int i = 0; i < shortPath.size(); ++i)
        {
     
            cout<<"("<<shortPath[i][0]<<","<<shortPath[i][1]<<")"<<endl;
        }
    }
    return 0;
}