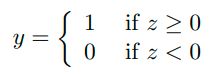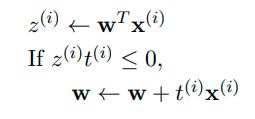线性模型+非线性=神经网络

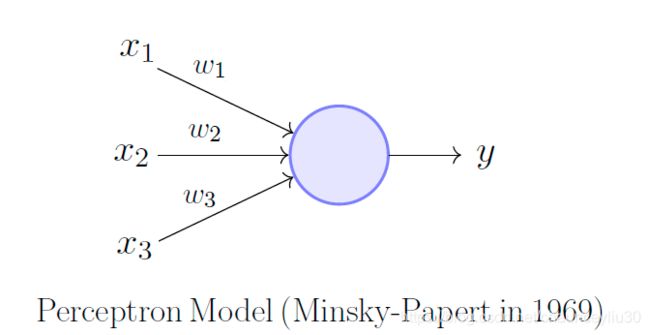
感知机（Perceptron）

---

                                                     

线性分类问题（Linear Classification）

说起单层感知机，首先要从线性二分类问题谈起。什么是线性二分类问题呢，首先数据在数据空间中应该是线性可分的，即可用一条直线（在几何空间中应为超平面）把不同类的数据分割开，而这条直线（超平面）就叫做决策边界（Decision Boundary)。其次数据空间中数据的类别数应为两种，而这两种类别通常被称为正例（positive）和反例（negative）。

决策边界的表达式：

判定决策结果：

为了计算的简便，我们通常在特征向量前加入一个虚拟特征（dummy feature），并在权重向量前加入一个，这样我们就可以在决策边界的表达式中省去偏差（bias）这一项。此时我们的决策边界表达式变为：

感知机学习规则

在感知机中，我们通常把正例和反例表示为1和-1，因为这种表达形式更有利于推导感知机的学习规则，看完下面的内容你就会明白为什么。现在我们的决策结果表达式变为：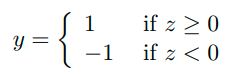

对于分类模型，我们如何判断模型分类的结果和真正的类别是否一致呢？需要用到下面的关系：。对于任一和原数据标签，若判定结果与数据标签相同，则两者相乘恒大于零，否则两者恒小于零。利用这一关系，若小于零（为-1），但数据标签为1，则需要增大使其大于零。为了增大，则需要增大权重向量，表达式为：更新后表达式为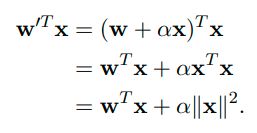：  反之亦然。

仔细观察我们可以发现的符号和原数据中标签符号相同，则可以用原数据中标签代替，于是权重系数更新的最终表达式为：

总结之前的步骤，则感知机学习规则的算法可表达为：

感知机应用

下面我们来编写一个用感知机学习规则来分类的方法并用它来验证单层感知机在线性模型和非线性模型中的效果。

from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
#使用sklearn自带的iris data中前100行数据
iris = load_iris()
iris_data = pd.DataFrame(data=iris.data,columns=iris['feature_names'])
iris_data["target"] = iris['target']
#为了可视化仅使用前两个特征
sepal_len = iris['data'][:100,0]
sepal_wid = iris['data'][:100,1]
labels = iris['target'][:100]
#使用均值标准化特征
sepal_len -= np.mean(sepal_len)
sepal_wid -= np.mean(sepal_wid)
#绘制散点图
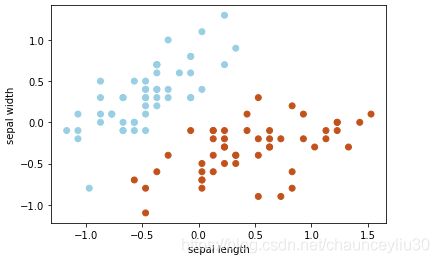
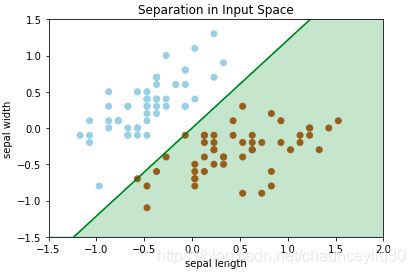
plt.scatter(sepal_len,sepal_wid,c=labels,cmap=plt.cm.Paired)
plt.xlabel("sepal length")
plt.ylabel("sepal width")

由图可观察到，该数据集是线性可分的，下面就来编写使用感知机学习规则来计算决策边界的方法。

#为了使用感知机学习规则需要把目标标签改为（-1，1）
sgn_labels=labels.copy()
for i in range(0,sgn_labels.size,1):
  if sgn_labels[i] == 0:
    sgn_labels[i]=-1
#计算超平面中权重W的方法
def plr2d_vectorize(X ,T, N):
    
    import numpy as np
    #创建所有元素为0的W矩阵
    W=np.zeros(X.shape[1]+1).reshape(-1,1)
    #在X向量前插入一列1
    X_prime=np.column_stack((np.ones(X.shape[0]),X))
    if T.ndim == 1:
        T=T.reshape(-1,1)
    #计算Z=W.T·X
    Z=np.dot(X_prime,W)
    #计算M=Z*T
    multiplication=Z*T
    #遍历M向量，若其中有负值则用感知机学习规则更新W
    #使用更新后的W重新计算Z和M
    #再遍历M并重复以上步骤
    #直到M中所有元素都为正或达到最大迭代次数
    for n in range(0,N):
        mismatch=False
        for i in range(0,T.shape[0]):
            if multiplication[i] <= 0:
                mismatch=True
                W=W+((X_prime[i]*T[i]).T).reshape(-1,1)
                Z=np.dot(X_prime,W)
                multiplication=Z*T
        if mismatch==False:
            break
    #若M向量中有负值，则打印该负值对应的索引（即没有被正确分类的数据索引）
    for i in range(0,T.shape[0]):
        if multiplication[i] <= 0:
            print("mismatch[",i,"]")

    return W

其中X是一个N*D维的矩阵，N为样本数，D为特征数，T是一个N*1的向量，N为最大迭代次数，若数据为线性不可分则迭代会在最大迭代次数停下。

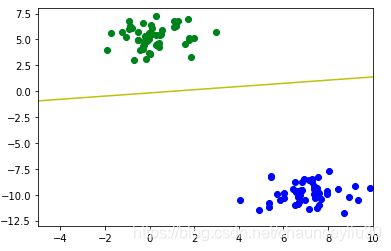
使用plr2d_vectorize(X,T,D)计算出W后绘制决策边界如下：

可以看出感知机模型正确计算出了决策边界，下面再通过python.datasets的数据生成功能分别生成线性可分和线性不可分数据来测试感知机的效果。

#该数据集为线性可分
X, y = datasets.make_blobs(n_samples=100,n_features=2,centers=2,random_state=14)
for i in range(0,y.size):
  if y[i] == 0:
      y[i]=-1
x=np.array(X.data)
t=np.array(y.data)
w=plr2d_vectorize(x,t,10)
m= -float(w[1])/float(w[2])
b=-float(w[0])/float(w[2])
plt.plot(X[:, 0][y == -1], X[:, 1][y == -1], 'go')
plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], 'bo')
plt.xlim(-5,10)
plt.ylim(-13,8)
plt.plot([-5,10],[-5*m+b, 10*m+b],'-y')
plt.show()

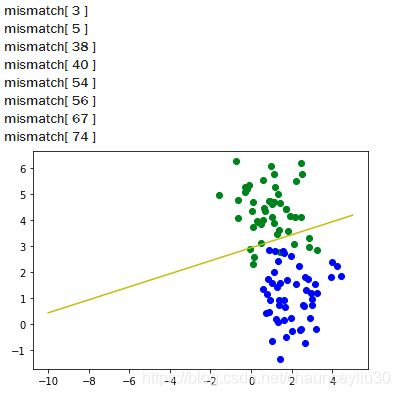
#该数据集为线性不可分
X, y = datasets.make_blobs(n_samples=100,n_features=2,centers=2,random_state=0)
for i in range(0,y.size):
  if y[i] == 0:
    y[i]=-1
x=np.array(X.data)
t=np.array(y.data)
w=plr2d_vectorize(x,t,10)
m= -float(w[1])/float(w[2])
b=-float(w[0])/float(w[2])
plt.plot(X[:, 0][y == -1], X[:, 1][y == -1], 'go')
plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], 'bo')
plt.plot([-10,5],[-10*m+b, 5*m+b],'-y')
plt.show()

可以看出对线性不可分数据，感知机在达到最大迭代次数时也无法正确分类所有数据。

逻辑回归（Logistic Regression）

---

优化问题（梯度下降）

从以上内容可以总结出单个感知机对于线性不可分的数据并没有起到很好的作用，而在生活中大部分的问题都是线性不可分的，对于像单层感知机这样简单的模型在实际操作中作用确实不大。另外，从感知机学习规则中可以看出权重的调整完全依赖于标签和数据，这种迭代方式随机性太强并不利于我们建造一个稳定的模型。作为机器学习中最为重要的思想之一，梯度下降可以解决大部分机器学习模型的优化问题。梯度下降的好处在于对于一个凸型损失函数，对其任意一点求导即可找出移动至最近的局部最小值的方向，而且离局部最小值越远每一步下降的越快。而使用梯度下降的一个局限就是损失函数必须处处可导。对于感知机模型来说，这显然不成立，因为其决策结果表达式为阶跃函数。那么有没有办法可以用一个可导的函数来替代这个阶跃函数呢？

逻辑函数（logistic function）

事实上存在一类叫做sigmoid的函数，他们的图像为S型，因此满足处处可导的条件，而用于逻辑回归的函数就属于这一类，它叫做逻辑方程。逻辑方程的表达式为：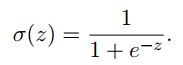

图像为：

可以看出当Z值趋近于无穷时，逻辑方程取得值近似于1，当Z值趋近于负无穷时，逻辑方程取得值近似于0，这与之前的阶跃函数功能相似，但不同的是该函数处处可导， 用该函数来取代感知机的阶跃函数，就离使用梯度下降更近了一步。

损失函数

为了使用梯度下降，最关键的步骤就是构造损失函数。如果使用线性回归使用的平方误差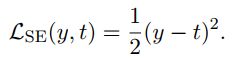，虽然构造出来的函数也处处可导，但有一个很关键的问题。使用该损失函数对z求导，得到结果为，当为1，也为（无限接近）1时，梯度为0，这符合我们对梯度下降的预期，然而当为（无限接近）于0时，得到的梯度竟也为0，这证明该损失函数的表现不符合我们对梯度下降的预期。于是就可以引出我们的交叉熵损失函数（cross-entropy loss)：

逻辑回归

使用了上述的逻辑函数和损失函数的模型就叫做逻辑回归模型，虽然叫做回归模型，但其实它是一种分类模型。而它正是使用了梯度下降方法来寻找最佳的权重向量，因此它的抗噪声干扰能力较强，对于非线性可分的数据也有较好的表现。

多层感知机（神经网络）

---

通过之前的感知机模型和逻辑回归模型，我们可以发现通过对线性模型和非线性的模型的组合能够使处理非常复杂的数据，而单纯的线性模型组合是无法达到这种效果的，因为任意线性模型的组合都可以通过合并同类项来组合成一个大的线性模型，因此不管是多个线性模型还是一个线性模型其表达效果都是相同的。而加入了非线性模型后，整体模型就可以表达更复杂的关系。（如果对这一点理解不是很透彻的读者可以参考经典的构造AND, OR, NOT 以及 XOR模型的例子，其中的XOR就无法使用线性关系来表达）

多层感知机就是通过以上表达的思想来构造一个含有多个层次，每一层包含多个感知机的模型。而现在一个大型的多层感知机又有了一个新的名字：神经网络。

其实神经网络的基本思想并不复杂，而著名的反向传播算法也只不过是微积分中的链式法则，虽然现在的研究人员给了这些方法新的名字但其内里还是亘古不变的也是非常基础的数学思想。

在神经网络中最重要的一点也是神经网络之所以这么强大的原因就是它的自由度。举例来说，对一个只有一个隐藏层的神经网络，若输入是一个N*D的矩阵，隐藏层中有H个神经元，输出层有k个类别，那么该神经网络的自由度就为。也就是说对于一个如此简单的神经网络，其中可调的参数就有这么多，每次对参数的调整都会影响每一层的表达，这也就是神经网络对复杂关系的表达能力如此之强的根本原因。