翻译：如何理解梯度下降算法Gradient Descent algorithm

在数据科学中，梯度下降Gradient Descent algorithm是重要且困难的概念之一。在这里，我们以非常简单的方式通过一个示例来解释这个概念。看一下这个。

贾纳维·马哈坦（Jahnavi Mahanta）。

当我第一次开始学习机器学习算法时，要弄清算法的作用是一项艰巨的任务。不仅因为很难理解所有的数学理论和符号，而且还很无聊。当我转向在线教程寻求答案时，我只能再次看到方程式或高级解释，而在大多数情况下都无需进行详细介绍。

那时，我的一位数据科学同事向我介绍了在Excel工作表中制定算法的概念。这为我创造了奇迹。任何新算法，我都会尝试在一个很小的范围内以精益求精的方式学习，并相信我，它确实在增强您的理解力，并帮助您充分理解算法的美感。

让我用一个例子向您解释。

大多数数据科学算法都是优化问题，而最常用的算法之一就是梯度下降算法。

现在，对于初学者来说，名称“梯度下降算法”本身可能听起来很吓人，希望在经过这篇文章后，它可能会改变。

让我们以通过住房数据预测新价格的示例为例：

现在，给定历史房屋数据，任务是创建一个模型，该模型在给定房屋大小的情况下预测新房屋的价格。

任务–对于一栋新房子，给定其大小（X），其价格（Y）将是多少？

让我们从绘制历史住房数据开始：

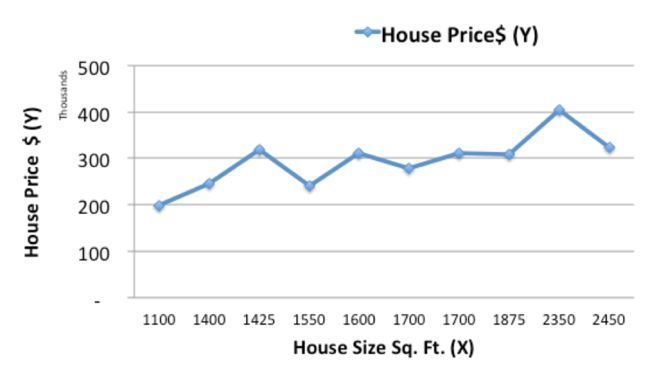
现在，我们将使用简单的线性模型（在历史数据上拟合一条线）来预测给定大小（X）的新房子（Ypred）的价格

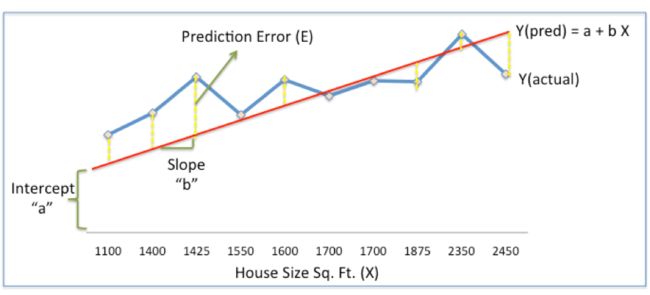
在上面的图表中，红线给出了给定房屋大小（X）时的预计房价（Ypred）。

Ypred = a + bX

蓝线提供了历史数据中的实际房价（实际）

Yactual和Ypred之间的差异（由黄色虚线给出）是预测误差（E）

因此，我们需要找到一条具有最佳a，b值（称为权重）的线，以减少预测误差并提高预测精度，从而最适合历史数据。

因此，我们的目标是找到使房屋实际价格和预测价格之间的误差最小的最佳a，b（1/2出于数学上的便利，因为它有助于计算微积分中的梯度）

平方误差总和（SSE）

Sum of Squared Errors (SSE) = ½ Sum (Actual House Price – Predicted House Price)2

=  ½ Sum(Y – Ypred)2

（请注意，还有其他度量错误的方法。SSE只是其中一种。）

这是渐变下降出现的地方。梯度下降是一种优化算法，可找到减少预测误差的最佳权重（a，b）。

现在让我们逐步了解梯度下降算法：

1. 步骤1：使用随机值初始化权重（a和b），然后计算误差（SSE）

2. 步骤2：计算梯度，即当权重（a和b）从其原始随机初始化值改变很小的值时，SSE的变化。这有助于我们在使SSE最小化的方向上移动a和b的值。

3. 步骤3：使用梯度调整权重以达到最佳值，其中SSE最小化

4. 步骤4：使用新的权重进行预测并计算新的SSE

5. 步骤5：重复步骤2和3，直到进一步调整权重不会显着减少错误为止

现在，我们将详细介绍每个步骤（我在excel中制定了步骤，粘贴在下面）。但是在此之前，我们必须对数据进行标准化，因为它会使优化过程更快。

步骤1：要拟合Ypred = a + b X线，请从a和b的随机值开始，然后计算预测误差（SSE）

步骤2：计算权重的误差梯度

∂SSE/∂a= –（Y-YP）

∂SSE/∂b= –（Y-YP）X

在此，SSE = 1/2（Y-YP）2 = 1/2（Y-（a + bX））2

您需要了解一些微积分，仅此而已！！

∂SSE/∂a和∂SSE/∂b是梯度，它们给出了a，b wrt到SSE的运动方向。

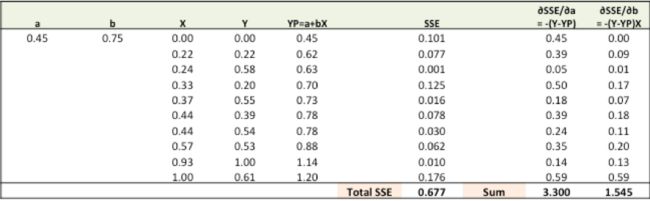
步骤3：使用梯度调整权重以达到最佳值，其中SSE最小化

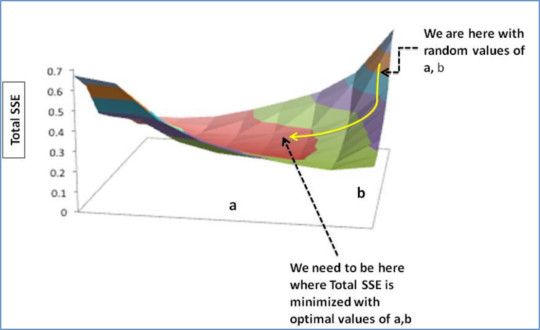
我们需要更新a，b的随机值，以便我们朝最佳a，b的方向移动。

更新规则：

a –∂SSE/∂a

b –∂SSE/∂b

因此，更新规则：

1. 新的a = a – r * ∂SSE/∂a= 0.45-0.01 * 3.300 = 0.42
2. 新的b = b – r * ∂SSE/∂b= 0.75-0.01 * 1.545 = 0.73
   在这里，r是学习率= 0.01，这是权重调整的速度。

步骤4：使用新的a和b进行预测并计算新的总SSE

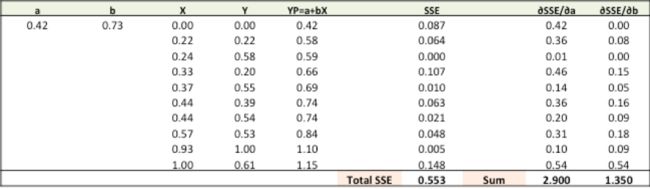
您可以通过新的预测看到，总的SSE下降了（0.677至0.553）。这意味着预测准确性已经提高。

第5步：重复第3步和第4步，直到进一步调整到a，b的时间不会显着减小误差为止。那时，我们已经得出了具有最高预测精度的最优a，b。

这是梯度下降算法。该优化算法及其变体构成了许多机器学习算法（如神经网络乃至深度学习）的核心

免责声明：

请注意，这篇文章主要是出于教程目的，因此：

1. 所使用的数据是虚拟的，数据大小非常小。同样为了简化示例，数据和模型是一个可变示例。
2. 这篇文章的主要目的是强调我们如何通过在excel中解决问题来简化对Gradient descent等算法背后的数学运算的理解，因此，这里没有人声称与最小二乘回归相比，gradient descent可以提供更好的/更差的结果。
3. 由于数据非常小，出于教程目的，整个数据都用于培训。但是，在构建实际的预测模型时，会利用各种数据验证技术（示例–训练/测试拆分或N交叉验证）

参考

https://www.kdnuggets.com/2017/04/simple-understand-gradient-descent-algorithm.html