Python神经网络学习--神经网络知识先导（二）--分类器是什么东西？

回顾

上期正式开启了神经网络的内容，讲了很少的东西，感谢大家的点赞评论收藏。

上期中我们做了个例子：一个单独的神经元，输入摄氏度，输出华氏度。

在模拟的神经元中，输入一个确定的摄氏度值后，得到的华氏度的输出不一定和真正的对应华氏度一样，所以，准确来讲，上期讲到的神经元属于预测器！

前言

预测器和分类器并无太大区别，但是找例子确实不好找。520那天，我看到了自己家院子里的月季，想到有一部分人确实不知道怎么区分玫瑰和月季以至于情人节买的玫瑰花实际上都是月季花，这次，就以这个的分类来讲一个分类器的例子吧。

事实上，月季和玫瑰很好辨认，只需要辨认花茎上的刺的数量和大小即可，月季的花茎上刺大，少；玫瑰花茎上刺小，密。如此，便找到了用于分类的特征，下一步，就可以“训练一个”分类器，送玫瑰之前扔进去辨别一下到底是不是玫瑰花即可。

训练玫瑰、月季分类器

准备数据

同样，训练之前需要去找一些数据，正好我家院子里常年种着月季花，地里也有一亩玫瑰，随便测量了几组大概数据（由于是讲解，能明白原理即可，所以并未测量许多也并不精确测量，就目测了一下）：

编号	数量（个）/ 单位茎长	平均大小（毫米）/ 刺	类别
1	11	0.9	玫瑰
2	13	0.8	玫瑰
3	17	0.9	玫瑰
4	4	2	月季
5	5	1.6	月季
6	5	1.8	月结

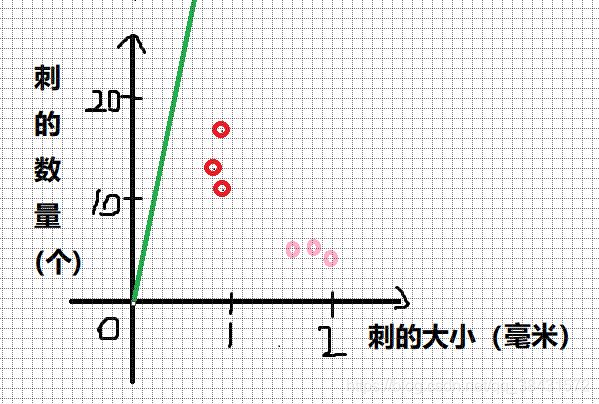
由于有两个因素，放在坐标系中可能会更清楚，所以放在坐标系内，画到坐标系中如图所示：

当然，我们人眼一眼能看出来一道分界线，能很清晰的分清楚这两种花，但是，我们大脑已经被我们训练了几十年，当然这种简单的分类已经可以很轻易的计算了，要记住，我们是从零开始训练这个神经网络的，如同一个婴儿无法分辨世界一般（如同婴儿无法聚焦眼睛，视野范围有限一般）。

初始网络

依据习惯，我们把横坐标轴称为x轴，纵坐标轴称为y轴，初始随机一条直线：

那么，这个直线的初始斜率，我就随机设置为51.47。即这条直线的初始预设为：y = 51.47 * x。 

注意：

1. 这并不意味着刺的大小和数量之间有数学上的线性关系，而是我们需要用一条直线对月季和玫瑰进行分类，而我们把刺的大小映射为了x，把刺的数量映射到了y，训练这个神经网络在这个例子中相当于找到这个直线的斜率。

2. 上期讲过，如果我们不能客观的取一个初始值，那么随机一个是比较好的解决方案。(为什么随即范围是0.1到100，如图，同样长度的坐标轴，y轴是10，x轴是1，这点是要人工调整的)。

3. 为什么过原点？因为简单！

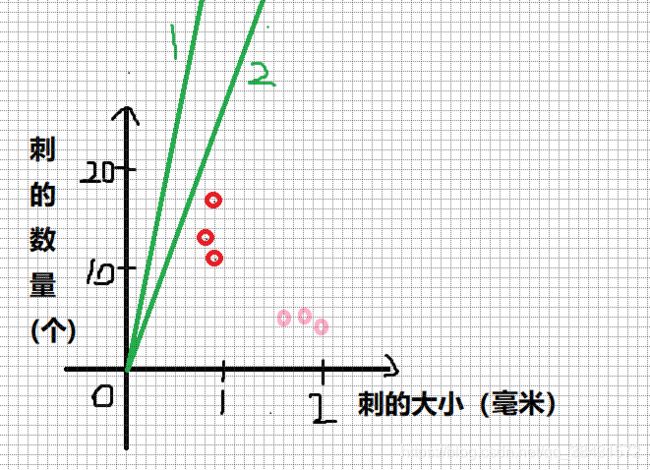
这个初始斜率映射到坐标中是这样的：

这个直线真是太糟糕了，根本没有完成任何的分类任务，要立马对它进行训练了。

开始训练

初始数据有了，初始网络有了，下一步就要去训练它了。为了节省篇章，这里就刻意挑选几个数据对网络训练，目的是为了让大家理解，而真正训练时应该顺序或者随机选数据。

做一点简单的数学

我们拿到了一个例子：（2，4），准备对网络训练，在这之前，需要先做一点中数学题。

我们目标是为了能分类这就要求有一条直线把两类花区分开需要通过调整直线斜率来达到这一目的。但是，要如何调整斜率呢？

以本例为例，我们需要达到输入x，输出y与4接近，不妨就令：x=2时，输出y为4，这就是我们需要的输入x = 2,目标输出ty = 4。

而实际上 y = C * x，（本例中随机的C=51.47）。

y与ty中间肯定是有误差的，根据上一期中，误差 = 目标值 - 计算值。就知道

误差 = ty - y。（即 E = ty - y）

而ty = C1 * x <==> ty = (C + Ce) * x，y = C * x。（C1 = C + Ce）(Ce是系数C的误差)

可以得到：E = ty - y = (C + Ce) * x - C * x = Ce * x。也就是说：E = Ce * x

等价于：Ce = E / x。（即：系数的误差 = 计算误差 / 输入x）

也就是说，我们只需要拿着计算误差除以输入就可以得到我们需要对系数调整的数值了，这就是训练这个网络的关键所在了！！！！！！！！

开始训练了

拿出来我们的数据（2，4），同上一期一样，代入x=2，2 * 51.47 = 102.94

而我们的目标值是4，但其实我要取3.9，并不取4，这点一会儿再说。

目标值是3.9，计算值是102.94，误差 = 目标值 - 计算值 = 3.9 - 102.94 = -99.04。（误差可正可负可为0）

希望你不要忘记：上期中说过，误差我们只需要取一小部分比如1%即可，不需要取很多，取得多了反而不好，但是鉴于这个例子中，百分之1的变化，这么几个例子看不出效果，所以我选取误差的50%。

-99.04 * 50%= -49.52这就是我们实际上要用到的误差。

根据我们上文得到的公式：Ce = E / x。

也就是说，我们的系数C（也就是本例中的51.47）需要改变的量Ce = -49.52 / 2 = -24.76。

C = 51.47 + (-24.76) = 26.71

那么，现在来看看我们得到的什么直线：

我们发现，这条直线向着正确的方向走了一步，尽管走的较少，但是如果训练样本给够，一定可以训练出一条直线，将这两种花完美分类出去。

动手实践

后面的步骤都大同小异，就是一些算术，有兴趣的同学可以自行计算一下，这里就不再和上一期一样把数据全部计算完毕了，很抱歉。

一些要点

偏置值

上面训练中，大家可能注意到，在选了数据（2，4）后，我使用的目标输出却是3.9，没使用4这个值，为什么呢？

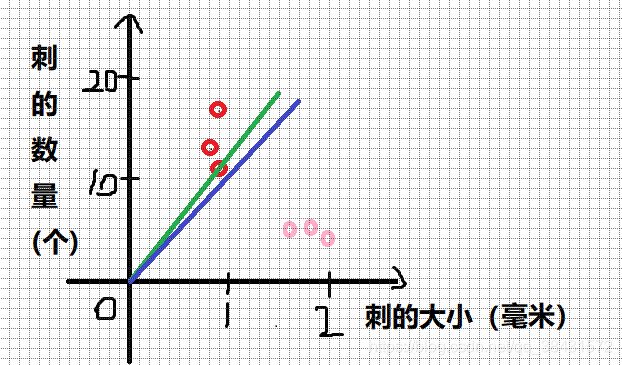
如下图：

 

大家觉得，如果要画一条分类用的直线，绿色的线和蓝色的线哪个更加好一点呢？

恐怕绿色的线自己也不知道被压的那个红色点是哪一类的吧。

这就是偏置值的作用，也可以理解为“矫枉过正”。

学习率

其实学习率可以不固定，比如第一次学习100%的误差，第二次学习50%的误差，第三次学习1/3的误差。。。。。如此下去，

或者其他算法，一般来讲，都是可以的。

多分类问题

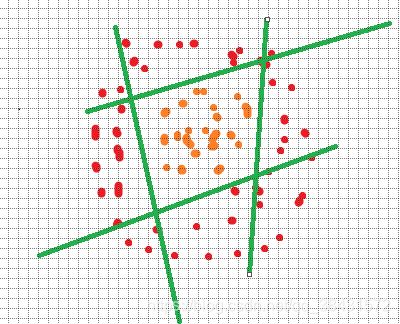
有时候，很多问题不是二分类的，而是多分类的，甚至二分类问题有时也无法用一条线分开，比如：

这种情况也很简单，只需要多画几条线即可：

只需要联想程序中的多重if语句，哈哈哈哈哈还是可以理解的。

总结

今天内容并不是太多太难，有一部分与上期的知识重合，这次主要是为了理清楚二分类的简易分类器以及一些要点（同样也是神经网络编程的要点）。

希望这次博文能够帮助到大家。

下期再见，谢谢观看！！