欧式空间——标椎正交基
文章目录
-
- 标准正交基
- Gram-Schmidt 正交化方法
- 正交矩阵
- 欧氏空间上的同构
- 参考
标准正交基
约定 : V : V :V 是欧氏空间
α 与 β 正交 : ( α , β ) = 0 ⇔ α T β = 0 \alpha \text { 与 } \beta \text { 正交 }:(\alpha, \beta)=0 \Leftrightarrow \alpha^{T} \beta=0 α 与 β 正交 :(α,β)=0⇔αTβ=0
正交向量组: α 1 , α 2 , ⋯ , α s \alpha_{1}, \alpha_{2}, \cdots, \alpha_{s} α1,α2,⋯,αs 两两正交且不含零向量.
如: α 1 = ( 1 , 1 , 1 ) , α 2 = ( − 1 , 2 , − 1 ) , α 3 = ( − 1 , 0 , 1 ) \text { 如: } \alpha_{1}=(1,1,1), \alpha_{2}=(-1,2,-1), \alpha_{3}=(-1,0,1) 如: α1=(1,1,1),α2=(−1,2,−1),α3=(−1,0,1)
标准向量组:每个向量的长度均为1.
标准正交向量组:正交向量组且为标准向量组
如: β 1 = ( 1 , 0 , 0 ) , β 2 = ( 0 , 2 / 2 , 2 / 2 ) \text { 如: } \beta_{1}=(1,0,0), \beta_{2}=(0, \sqrt{2} / 2, \sqrt{2} / 2) 如: β1=(1,0,0),β2=(0,2/2,2/2)
标准正交基:正交向量组,标准向量组且为基
如: ε 1 = ( 1 , 0 , 0 ) , ε 2 = ( 0 , 1 , 0 ) , ε 3 = ( 0 , 0 , 1 ) \text { 如: } \varepsilon_{1}=(1,0,0), \varepsilon_{2}=(0,1,0), \varepsilon_{3}=(0,0,1) 如: ε1=(1,0,0),ε2=(0,1,0),ε3=(0,0,1)
例 1 \Large{\color{violet}{例1}} 例1 . 设 A A A 是 n n n 阶实反对称矩阵, x x x 是 n n n 维列向量,且 A x = y . A x=y . Ax=y. 证明: x x x 与 y y y 正交.
分析: \quad A反对称 ⇒ A T = − A \quad \Rightarrow A^{T}=-A ⇒AT=−A
x 与 y 正交? ⇔ ( x , y ) = 0 ? x \text { 与 } y \text { 正交? } \quad \Leftrightarrow(x, y)=0 ? x 与 y 正交? ⇔(x,y)=0?
证: ( x , y ) = x T y = x T A x \quad(x, y)=x^{T} y=x^{T} A x (x,y)=xTy=xTAx
两端同取转置
⇒ ( x , y ) = x T A T x = − x T A x = − x T y = − ( x , y ) ⇒ ( x , y ) = 0 ⇒ x 与 y 正交. \begin{array}{l} \Rightarrow(x, y)=x^{T} A^{T} x=-x^{T} A x=-x^{T} y=-(x, y) \\ \Rightarrow(x, y)=0 \Rightarrow x \text { 与 } y \text { 正交. } \end{array} ⇒(x,y)=xTATx=−xTAx=−xTy=−(x,y)⇒(x,y)=0⇒x 与 y 正交.
定理1. (1) α 1 , ⋯ , α s ∈ V \alpha_{1}, \cdots, \alpha_{s} \in V α1,⋯,αs∈V 是正交向量组 ⇒ α 1 , ⋯ , α s \Rightarrow \alpha_{1}, \cdots, \alpha_{s} ⇒α1,⋯,αs 线性无 关;
( 2 ) (2) (2) 若 I I I: α 1 , ⋯ , α n \alpha_{1}, \cdots, \alpha_{n} α1,⋯,αn 是 V V V 的一组基,则: I I I 是标准正交基 ⇔ V \Leftrightarrow V ⇔V 在基 I I I 下的度量矩阵为单位阵;
(3)若 I \mathbf{I} I 是标准正交基, α = ( α 1 , … , α n ) X , β = ( α 1 , … , α n ) Y \alpha=\left(\alpha_{1}, \ldots, \alpha_{n}\right) X, \beta=\left(\alpha_{1}, \ldots, \alpha_{n}\right) Y α=(α1,…,αn)X,β=(α1,…,αn)Y, 则
( α , β ) = X T Y = x 1 y 1 + ⋯ + x n y n (\alpha, \beta)=X^{T} Y=x_{1} y_{1}+\cdots+x_{n} y_{n} (α,β)=XTY=x1y1+⋯+xnyn
证明: (1)设 k 1 α 1 + k 2 α 2 + ⋯ + k s α s = 0 k_{1} \alpha_{1}+k_{2} \alpha_{2}+\cdots+k_{s} \alpha_{s}=0 k1α1+k2α2+⋯+ksαs=0,
两端同时与 α i ( 1 ≤ i ≤ s ) \alpha_{i}(1 \leq i \leq s) αi(1≤i≤s) 做内积:
⇒ k 1 ( α 1 , α i ) + k 2 ( α 2 , α i ) + ⋯ + k s ( α s , α i ) = ( 0 , α i ) = 0 \Rightarrow k_{1}\left(\alpha_{1}, \alpha_{i}\right)+k_{2}\left(\alpha_{2}, \alpha_{i}\right)+\cdots+k_{s}\left(\alpha_{s}, \alpha_{i}\right)=\left(0, \alpha_{i}\right)=0 ⇒k1(α1,αi)+k2(α2,αi)+⋯+ks(αs,αi)=(0,αi)=0
α 1 , ⋯ , α s \alpha_{1}, \cdots, \alpha_{s} α1,⋯,αs 是正交向量组 ⇒ ( α j , α i ) = 0 , ∀ j ≠ i , ( α i , α i ) ≠ 0 \Rightarrow\left(\alpha_{j}, \alpha_{i}\right)=0, \forall j \neq i, \quad\left(\alpha_{i}, \alpha_{i}\right) \neq 0 ⇒(αj,αi)=0,∀j=i,(αi,αi)=0
⇒ k i ( α i , α i ) = 0 ⇒ k i = 0 ( 1 ≤ i ≤ s ) ⇒ α 1 , ⋯ , α s 线 性 无 关 \begin{array}{l} \Rightarrow k_{i}\left(\alpha_{i}, \alpha_{i}\right)=0 \\ \Rightarrow k_{i}=0(1 \leq i \leq s)\\ \Rightarrow \alpha_{1}, \cdots, \alpha_{s} ~~ 线性无关 \end{array} ⇒ki(αi,αi)=0⇒ki=0(1≤i≤s)⇒α1,⋯,αs 线性无关
(2) α 1 , ⋯ , α n \alpha_{1}, \cdots, \alpha_{n} α1,⋯,αn 是标准正交基 ⇔ ( α i , α j ) = δ i j ⇔ ( ( α i , α j ) ) ⏟ 度量矩阵 = I \Leftrightarrow\left(\alpha_{i}, \alpha_{j}\right)=\delta_{i j} \Leftrightarrow \underbrace{\left(\left(\alpha_{i}, \alpha_{j}\right)\right)}_{\color{red}\text {度量矩阵 }}=I ⇔(αi,αj)=δij⇔度量矩阵 ((αi,αj))=I
( 3 ) ( α , β ) = ( ∑ i = 1 n x i α i , ∑ j = 1 n y j α j ) = ∑ i = 1 n ∑ j = 1 n x i y j ( α i , α j ) = ∑ i = 1 n x i y i ( α i , α i ) = ∑ i = 1 n x i y i = X T Y \begin{aligned}(\mathbf{3})(\alpha, \beta) &=\left(\sum_{i=1}^{n} x_{i} \alpha_{i}, \sum_{j=1}^{n} y_{j} \alpha_{j}\right)=\sum_{i=1}^{n} \sum_{j=1}^{n} x_{i} y_{j}\left(\alpha_{i}, \alpha_{j}\right) \\ &=\sum_{i=1}^{n} x_{i} y_{i}\left(\alpha_{i}, \alpha_{i}\right)=\sum_{i=1}^{n} x_{i} y_{i}=X^{T} Y \end{aligned} (3)(α,β)=(i=1∑nxiαi,j=1∑nyjαj)=i=1∑nj=1∑nxiyj(αi,αj)=i=1∑nxiyi(αi,αi)=i=1∑nxiyi=XTY
线性无关向量组未必是正交向量组.
如 : α 1 = ( 1 , 0 , 0 ) , α 2 = ( 1 , 1 , 0 ) , α 3 = ( 1 , 1 , 1 ) \text { 如 }: \alpha_{1}=(1,0,0), \alpha_{2}=(1,1,0), \alpha_{3}=(1,1,1) 如 :α1=(1,0,0),α2=(1,1,0),α3=(1,1,1)
例 2 \Large{\color{violet}{例2}} 例2 . 设 α 1 = ( 1 , 1 , 1 ) , α 2 = ( 1 , − 2 , 1 ) \alpha_{1}=(1,1,1), \alpha_{2}=(1,-2,1) α1=(1,1,1),α2=(1,−2,1), 求 α 3 \alpha_{3} α3, 使 α 1 , α 2 , α 3 \alpha_{1}, \alpha_{2}, \alpha_{3} α1,α2,α3 为正交向量组.
解: 设 α 3 = ( x 1 , x 2 , x 3 ) \alpha_{3}=\left(x_{1}, x_{2}, x_{3}\right) α3=(x1,x2,x3), 则:
( α 1 , α 3 ) = x 1 + x 2 + x 3 = 0 ( α 2 , α 3 ) = x 1 − 2 x 2 + x 3 = 0 ⇒ α 3 = ( 1 , 0 , − 1 ) \begin{array}{l} \left(\alpha_{1}, \alpha_{3}\right)=x_{1}+x_{2}+x_{3}=0 \\ \left(\alpha_{2}, \alpha_{3}\right)=x_{1}-2 x_{2}+x_{3}=0 \quad \Rightarrow \alpha_{3}=(1,0,-1) \end{array} (α1,α3)=x1+x2+x3=0(α2,α3)=x1−2x2+x3=0⇒α3=(1,0,−1)
Gram-Schmidt 正交化方法
定理2: 设 α 1 , ⋯ , α m \alpha_{1}, \cdots, \alpha_{m} α1,⋯,αm 是欧氏空间 V V V 中线性无关的向量组则存在 V V V 的标准正交向量组 γ 1 , ⋯ , γ m \gamma_{1}, \cdots, \gamma_{m} γ1,⋯,γm, 使得
span ( α 1 , ⋯ , α r ) = span ( β 1 , ⋯ , β r ) ( 1 ≤ r ≤ m ) \operatorname{span}\left(\alpha_{1}, \cdots, \alpha_{r}\right)=\operatorname{span}\left(\beta_{1}, \cdots, \beta_{r}\right)(1 \leq r \leq m) span(α1,⋯,αr)=span(β1,⋯,βr)(1≤r≤m)
正交化: 归纳法 r = 1 : β 1 = α 1 \quad \boldsymbol{r}=\mathbf{1}: \boldsymbol{\beta}_{1}=\alpha_{1} r=1:β1=α1
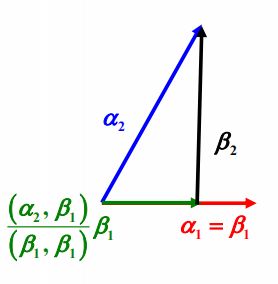
r = 2 : r=2: r=2: 取 β 2 = α 2 + k β 1 \beta_{2}=\alpha_{2}+k \beta_{1} β2=α2+kβ1, 选取适当的 k k k 使得 ( β 2 , β 1 ) = 0 \left(\beta_{2}, \beta_{1}\right)=0 (β2,β1)=0
( α 2 + k β 1 , β 1 ) = ( α 2 , β 1 ) + k ( β 1 , β 1 ) = 0 , ⇒ k = − ( α 2 , β 1 ) ( β 1 , β 1 ) , \begin{array}{r} \left(\alpha_{2}+k \beta_{1}, \beta_{1}\right)=\left(\alpha_{2}, \beta_{1}\right)+k\left(\beta_{1}, \beta_{1}\right)=0, \\ \Rightarrow k=-\frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)}, \end{array} (α2+kβ1,β1)=(α2,β1)+k(β1,β1)=0,⇒k=−(β1,β1)(α2,β1),
得到:
β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_{2}=\alpha_{2}-\frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1} β2=α2−(β1,β1)(α2,β1)β1
( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1} (β1,β1)(α2,β1)β1 是 α 2 \alpha_{2} α2 在 β 1 \beta_{1} β1 上的投影向量。
r = 3 : r=3: r=3: 令 β 3 = α 3 + k 1 β 1 + k 2 β 2 \beta_{3}=\alpha_{3}+k_{1} \beta_{1}+k_{2} \beta_{2} β3=α3+k1β1+k2β2, 求 k 1 , k 2 k_{1}, k_{2} k1,k2 使得 ( β 1 , β 3 ) = ( β 2 , β 3 ) = 0 \left(\beta_{1}, \beta_{3}\right)=\left(\beta_{2}, \beta_{3}\right)=0 (β1,β3)=(β2,β3)=0
0 = ( β 1 , β 3 ) = ( β 1 , α 3 ) + k 1 ( β 1 , β 1 ) ⇒ k 1 = − ( α 3 , β 1 ) ( β 1 , β 1 ) 0 = ( β 2 , β 3 ) = ( β 2 , α 3 ) + k 2 ( β 2 , β 2 ) ⇒ k 2 = − ( α 3 , β 2 ) ( β 2 , β 2 ) ⇒ β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 0=\left(\beta_{1}, \beta_{3}\right)=\left(\beta_{1}, \alpha_{3}\right)+k_{1}\left(\beta_{1}, \beta_{1}\right) \quad \Rightarrow k_{1}=-\frac{\left(\alpha_{3}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)}\\ 0=\left(\beta_{2}, \beta_{3}\right)=\left(\beta_{2}, \alpha_{3}\right)+k_{2}\left(\beta_{2}, \beta_{2}\right) \Rightarrow k_{2}=-\frac{\left(\alpha_{3}, \beta_{2}\right)}{\left(\beta_{2}, \beta_{2}\right)}\\ \Rightarrow \beta_{3}=\alpha_{3}-\frac{\left(\alpha_{3}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}-\frac{\left(\alpha_{3}, \beta_{2}\right)}{\left(\beta_{2}, \beta_{2}\right)} \beta_{2} 0=(β1,β3)=(β1,α3)+k1(β1,β1)⇒k1=−(β1,β1)(α3,β1)0=(β2,β3)=(β2,α3)+k2(β2,β2)⇒k2=−(β2,β2)(α3,β2)⇒β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
α 3 \alpha_{3} α3 分别减去其在 β 1 , β 2 \beta_{1}, \boldsymbol{\beta}_{2} β1,β2 上的投影向量.
一般地: 正交化:
β s = α s − ( α s , β 1 ) ( β 1 , β 1 ) β 1 − ( α s , β 2 ) ( β 2 , β 2 ) β 2 − ⋯ − ( α s , β s − 1 ) ( β s − 1 , β s − 1 ) β s − 1 2 ≤ s ≤ m \begin{array}{r} \beta_{s}=\alpha_{s}-\frac{\left(\alpha_{s}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}-\frac{\left(\alpha_{s}, \beta_{2}\right)}{\left(\beta_{2}, \beta_{2}\right)} \beta_{2}-\cdots-\frac{\left(\alpha_{s}, \beta_{s-1}\right)}{\left(\beta_{s-1}, \beta_{s-1}\right)} \beta_{s-1} \\ \\ 2 \leq s \leq m \end{array} βs=αs−(β1,β1)(αs,β1)β1−(β2,β2)(αs,β2)β2−⋯−(βs−1,βs−1)(αs,βs−1)βs−12≤s≤m
单位化:
令 γ i = 1 ∥ β i ∥ β i ( i = 1 , 2 , ⋯ , m ) , \text { 令 } \gamma_{i}=\frac{1}{\left\|\beta_{i}\right\|} \beta_{i} \quad(i=1,2, \cdots, m), 令 γi=∥βi∥1βi(i=1,2,⋯,m),
⇒ γ 1 , γ 2 , ⋯ , γ s \Rightarrow \gamma_{1}, \gamma_{2}, \cdots, \gamma_{s} ⇒γ1,γ2,⋯,γs 是标准正交向量组, 且
span ( α 1 , ⋯ , α r ) = span ( β 1 , ⋯ , β r ) \operatorname{span}\left(\alpha_{1}, \cdots, \alpha_{r}\right)=\operatorname{span}\left(\beta_{1}, \cdots, \beta_{r}\right) span(α1,⋯,αr)=span(β1,⋯,βr)
正交化:
β 1 = α 1 , β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 ⋯ … … … … … … … . β m = α m − ( α m , β 1 ) ( β 1 , β 1 ) β 1 − ⋯ − ( α m , β m − 1 ) ( β m − 1 , β m − 1 ) β m − 1 } ⇒ \left. \begin{array}{l}\beta_{1}=\alpha_{1}, \\ \beta_{2}=\alpha_{2}-\frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1} \\ \cdots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . \\ \beta_{m}=\alpha_{m}-\frac{\left(\alpha_{m}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}-\cdots-\frac{\left(\alpha_{m}, \beta_{m-1}\right)}{\left(\beta_{m-1}, \beta_{m-1}\right)} \beta_{m-1}\end{array}\right\}\Rightarrow β1=α1,β2=α2−(β1,β1)(α2,β1)β1⋯………………….βm=αm−(β1,β1)(αm,β1)β1−⋯−(βm−1,βm−1)(αm,βm−1)βm−1⎭⎪⎪⎪⎬⎪⎪⎪⎫⇒
⇒ ( α 1 , α 2 , ⋯ , α m ) = ( β 1 , β 2 , ⋯ , β m ) ( 1 ∗ ∗ ∗ 1 ∗ ∗ ⋱ ∗ O 1 ) \begin{array}{l} \Rightarrow\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{m}\right)=\left(\beta_{1}, \beta_{2}, \cdots, \beta_{m}\right)\left(\begin{array}{rrrr} 1 & * & * & * \\ & 1 & * & * \\ & & \ddots & * \\ O & & & 1 \end{array}\right) \end{array} ⇒(α1,α2,⋯,αm)=(β1,β2,⋯,βm)⎝⎜⎜⎛1O∗1∗∗⋱∗∗∗1⎠⎟⎟⎞
单位化:
γ i = 1 ∥ β i ∥ β i ⇒ ( β 1 , β 2 , ⋯ , β m ) = ( γ 1 , γ 2 , ⋯ , γ m ) ( ∥ β 1 ∥ o ∥ β 2 ∥ o ⋱ β m ∥ ) \quad \gamma_{i}=\frac{1}{\left\|\beta_{i}\right\|} \beta_{i} \Rightarrow\left(\beta_{1}, \beta_{2}, \cdots, \beta_{m}\right)=\left(\gamma_{1}, \gamma_{2}, \cdots, \gamma_{m}\right)\left(\begin{array}{ccc} \left\|\beta_{1}\right\| & & o \\ & \left\|\beta_{2}\right\| & & \\ o & & \ddots \beta_{m} \| \end{array}\right) γi=∥βi∥1βi⇒(β1,β2,⋯,βm)=(γ1,γ2,⋯,γm)⎝⎛∥β1∥o∥β2∥o⋱βm∥⎠⎞
( α 1 , α 2 , ⋯ , α m ) = ( β 1 , β 2 , ⋯ , β m ) ( 1 ∗ ∗ ∗ 1 ∗ ∗ ⋱ ∗ o 1 ) ( β 1 , β 2 , ⋯ , β m ) = ( γ 1 , γ 2 , ⋯ , γ m ) ( ∥ β 1 ∥ O ∥ β 2 ∥ ⋱ O ∥ β m ∥ ) \begin{array}{l} \left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{m}\right)=\left(\beta_{1}, \beta_{2}, \cdots, \beta_{m}\right)\left(\begin{array}{cccc} 1 & * & * & * \\ & 1 & * & * \\ & & \ddots & * \\ o & & & 1 \end{array}\right) \\ \left(\beta_{1}, \beta_{2}, \cdots, \beta_{m}\right)=\left(\gamma_{1}, \gamma_{2}, \cdots, \gamma_{m}\right)\left(\begin{array}{lll} \left\|\beta_{1}\right\| & & & O \\ & \left\|\beta_{2}\right\| & & \\ & & \ddots & \\ O & & & \left\|\beta_{m}\right\| \end{array}\right) \end{array} (α1,α2,⋯,αm)=(β1,β2,⋯,βm)⎝⎜⎜⎛1o∗1∗∗⋱∗∗∗1⎠⎟⎟⎞(β1,β2,⋯,βm)=(γ1,γ2,⋯,γm)⎝⎜⎜⎛∥β1∥O∥β2∥⋱O∥βm∥⎠⎟⎟⎞
⇒ ( α 1 , α 2 , ⋯ , α m ) ⏟ A = ( γ 1 , γ 2 , ⋯ , γ m ) ⏟ Q ( ∥ β 1 ∥ ∗ ∗ ∗ ∥ β 2 ∥ ∗ ∗ ⋱ ∗ O ∥ β m ∥ ) ⏟ R \Rightarrow \underbrace{\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{m}\right)}_{A}=\underbrace{\left(\gamma_{1}, \gamma_{2}, \cdots, \gamma_{m}\right)}_{Q} \underbrace{\left(\begin{array}{ccc} \left\|\beta_{1}\right\| & * & * & * \\ & \left\|\beta_{2}\right\| & * & * \\ & & \ddots & * \\ \boldsymbol{O} & & & \left\|\beta_{m}\right\| \end{array}\right)}_{\boldsymbol{R}} ⇒A (α1,α2,⋯,αm)=Q (γ1,γ2,⋯,γm)R ⎝⎜⎜⎛∥β1∥O∗∥β2∥∗∗⋱∗∗∗∥βm∥⎠⎟⎟⎞
A A A 可逆 ⇒ A = Q R , Q \Rightarrow A=Q R, Q ⇒A=QR,Q 正交, R R R 是正线上三角
例 3 \Large{\color{violet}{例3}} 例3. 将 α 1 = ( 1 , 1 , 1 ) , α 2 = ( 1 , 2 , 1 ) , α 3 = ( 0 , − 1 , 1 ) \alpha_{1}=(1,1,1), \alpha_{2}=(1,2,1), \alpha_{3}=(0,-1,1) α1=(1,1,1),α2=(1,2,1),α3=(0,−1,1) 标准正交化.
解: ( 1 ) \quad(1) (1) 正交化
β 1 = α 1 = ( 1 , 1 , 1 ) β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 = ( 1 , 2 , 1 ) − 4 3 ( 1 , 1 , 1 ) = 1 3 ( − 1 , 2 , − 1 ) , β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 = ⋯ = 1 2 ( − 1 , 0 , 1 ) \begin{array}{l} \beta_{1}=\alpha_{1}=(1,1,1) \\ \beta_{2}=\alpha_{2}-\frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}=(1,2,1)-\frac{4}{3}(1,1,1)=\frac{1}{3}(-1,2,-1), \\ \beta_{3}=\alpha_{3}-\frac{\left(\alpha_{3}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}-\frac{\left(\alpha_{3}, \beta_{2}\right)}{\left(\beta_{2}, \beta_{2}\right)} \beta_{2}=\cdots=\frac{1}{2}(-1,0,1) \end{array} β1=α1=(1,1,1)β2=α2−(β1,β1)(α2,β1)β1=(1,2,1)−34(1,1,1)=31(−1,2,−1),β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2=⋯=21(−1,0,1)
(2) 单位化
γ 1 = 1 ∥ β 1 ∥ β 1 = 1 3 ( 1 , 1 , 1 ) γ 2 = 1 6 ( − 1 , 2 , − 1 ) γ 3 = 1 2 ( − 1 , 0 , 1 ) . \gamma_{1}=\frac{1}{\left\|\beta_{1}\right\|} \beta_{1}=\frac{1}{\sqrt{3}}(1,1,1) \quad \gamma_{2}=\frac{1}{\sqrt{6}}(-1,2,-1) \quad \gamma_{3}=\frac{1}{\sqrt{2}}(-1,0,1) . γ1=∥β1∥1β1=31(1,1,1)γ2=61(−1,2,−1)γ3=21(−1,0,1).
注意: 将 β = k α ( k > 0 ) \beta=k \alpha(k>0) β=kα(k>0) 单位化,只需将 α \alpha α 单位化即可.
正交矩阵
正交矩阵: 实方阵 A A A 满足 A A T = A T A = I ( A A^{T}=A^{T} A=I\left(\right. AAT=ATA=I( 等价于 A T A = I ) . \left.A^{T} A=I\right) . ATA=I).
定理3: 设 A , B ∈ R n × n A, B \in \mathbb{R}^{n \times n} A,B∈Rn×n 是正交矩阵,则
(1) ∣ A ∣ = ± 1 |A|=\pm 1 ∣A∣=±1, 特别地 A A A 可逆;
(2) A B , A T = A − 1 , A ∗ A B, A^{T}=A^{-1}, A^{*} AB,AT=A−1,A∗ 正交;
设 V V V 是 n n n 维欧氏空间,则
(3) 两组标准正交基之间的过渡矩阵是正交矩阵;
证明: (1) A A T = I ⇒ 1 = ∣ I ∣ = ∣ A A T ∣ = ∣ A ∣ 2 ⇒ ∣ A ∣ = ± 1. A A^{T}=I \Rightarrow 1=|I|=\left|A A^{T}\right|=|A|^{2} \Rightarrow|A|=\pm 1 . AAT=I⇒1=∣I∣=∣∣AAT∣∣=∣A∣2⇒∣A∣=±1.
(2) A , B 正交 ⇒ A T A = I = B T B ⇒ ( A B ) T ( A B ) = B T A T A B = B T B = I ⇒ A B 正交 A 正交 ⇒ I = A A T = ( A T ) T A T ⇒ A T 正交 A ∗ = ∣ A ∣ A − 1 = ∣ A ∣ A T ⇒ ( A ∗ ) T A ∗ = ∣ A ∣ 2 A A T = I ⇒ A ∗ 正交. \begin{array}{l}\text { (2) } A, B \text { 正交 } & \Rightarrow A^{T} A=I=B^{T} B \\ & \Rightarrow(A B)^{T}(A B)=B^{T} A^{T} A B=B^{T} B=I \Rightarrow A B \text { 正交 } \\ A \text { 正交 } & \Rightarrow I=A A^{T}=\left(A^{T}\right)^{T} A^{T} \Rightarrow A^{T} \text { 正交 } \\ A^{*}=|A| A^{-1}= & |A| A^{T} \Rightarrow\left(A^{*}\right)^{T} A^{*}=|A|^{2} A A^{T}=I \Rightarrow A^{*} \text { 正交. }\end{array} (2) A,B 正交 A 正交 A∗=∣A∣A−1=⇒ATA=I=BTB⇒(AB)T(AB)=BTATAB=BTB=I⇒AB 正交 ⇒I=AAT=(AT)TAT⇒AT 正交 ∣A∣AT⇒(A∗)TA∗=∣A∣2AAT=I⇒A∗ 正交.
(3) 设 I I I: α 1 , ⋯ , α n \alpha_{1}, \cdots, \alpha_{n} α1,⋯,αn 与 I I II II: β 1 , ⋯ , β n \beta_{1}, \cdots, \beta_{n} β1,⋯,βn 都是欧氏空间 V V V 的标准正交基.
由
- V V V 在标准正交基 I I I下的度量矩阵为单位阵: A = I A=I A=I 。
- V V V 在标准正交基 I I II II 下的度量矩阵为单位阵: B = I B=I B=I
- 设从基I 到基 II 的过渡矩阵 C C C
可以得到: ⇒ I = B = C T A C = C T C \Rightarrow I=B=C^{T} A C=C^{T} C ⇒I=B=CTAC=CTC
⇒ \Rightarrow ⇒ 过渡矩阵 C C C 正交
定理4. 设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n, 则 A A A 正交 ⇔ A \Leftrightarrow A ⇔A 的行 ( ( ( 列 ) ) ) 组关于 R 1 × n ( R n × 1 ) \mathbb{R}^{1 \times n}\left(\mathbb{R}^{n \times 1}\right) R1×n(Rn×1) 是标准正交组.
证明: 设 A = ( α 1 , ⋯ , α n ) A=\left(\alpha_{1}, \cdots, \alpha_{n}\right) A=(α1,⋯,αn), 则
A 正交 ⇔ A T A = I ⇔ I = ( α 1 T ⋮ α n T ) ( α 1 , ⋯ , α n ) = ( α 1 T α 1 ⋯ α 1 T α n ⋮ ⋱ ⋮ α n T α 1 ⋯ α n T α n ) ⇔ α i T α i = 1 , α i T α j = 0 ( ∀ i ≠ j ) ⇔ ( α i , α i ) = 1 , ( α i , α j ) = 0 ( ∀ i ≠ j ) ⇔ A 的 列 组 关 于 R n × 1 是 标 准 正 交 组 . \begin{aligned} A \text { 正交 } \Leftrightarrow A^{T} A=I & \Leftrightarrow I=\left(\begin{array}{c} \alpha_{1}^{T} \\ \vdots \\ \alpha_{n}^{T} \end{array}\right)\left(\alpha_{1}, \cdots, \alpha_{n}\right)=\left(\begin{array}{ccc} \alpha_{1}^{T} \alpha_{1} & \cdots & \alpha_{1}^{T} \alpha_{n} \\ \vdots & \ddots & \vdots \\ \alpha_{n}^{T} \alpha_{1} & \cdots & \alpha_{n}^{T} \alpha_{n} \end{array}\right) \\ & \Leftrightarrow \alpha_{i}^{T} \alpha_{i}=1, \quad \alpha_{i}^{T} \alpha_{j}=0(\forall i \neq j) \\ & \Leftrightarrow\left(\alpha_{i}, \alpha_{i}\right)=1,\left(\alpha_{i}, \alpha_{j}\right)=0(\forall i \neq j) \\ &\Leftrightarrow A 的列组关于 \mathbb{R}^{n \times 1} 是标准正交组. \end{aligned} A 正交 ⇔ATA=I⇔I=⎝⎜⎛α1T⋮αnT⎠⎟⎞(α1,⋯,αn)=⎝⎜⎛α1Tα1⋮αnTα1⋯⋱⋯α1Tαn⋮αnTαn⎠⎟⎞⇔αiTαi=1,αiTαj=0(∀i=j)⇔(αi,αi)=1,(αi,αj)=0(∀i=j)⇔A的列组关于Rn×1是标准正交组.
同理可证行组的情形.
例 1 \Large{\color{violet}{例1}} 例1 设 A = ( α 1 , α 2 , α 3 ) A=\left(\alpha_{1}, \alpha_{2}, \alpha_{3}\right) A=(α1,α2,α3) 为正交矩阵,
β 1 = 1 3 ( 2 α 1 + 2 α 2 − α 3 ) , β 2 = 1 3 ( 2 α 1 − α 2 + 2 α 3 ) , β 3 = 1 3 ( α 1 − 2 α 2 − 2 α 3 ) \beta_{1}=\frac{1}{3}\left(2 \alpha_{1}+2 \alpha_{2}-\alpha_{3}\right), \quad \beta_{2}=\frac{1}{3}\left(2 \alpha_{1}-\alpha_{2}+2 \alpha_{3}\right), \quad \beta_{3}=\frac{1}{3}\left(\alpha_{1}-2 \alpha_{2}-2 \alpha_{3}\right) β1=31(2α1+2α2−α3),β2=31(2α1−α2+2α3),β3=31(α1−2α2−2α3)
证明: B = ( β 1 , β 2 , β 3 ) \boldsymbol{B}=\left(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \boldsymbol{\beta}_{3}\right) B=(β1,β2,β3) 是正交矩阵.
方法 1 : 1: 1: 证明 ( β i , β j ) = 0 ( i ≠ j ) , ∥ β i ∥ = 1 , ( i = 1 , 2 , 3 ) . \left(\beta_{i}, \beta_{j}\right)=0(i \neq j),\left\|\beta_{i}\right\|=1,(i=1,2,3) . (βi,βj)=0(i=j),∥βi∥=1,(i=1,2,3).
( β 1 , β 1 ) = 1 9 ( 2 α 1 + 2 α 2 − α 3 , 2 α 1 + 2 α 2 − α 3 ) = 1 9 ( 4 + 4 + 1 ) = 1 ( β 1 , β 2 ) = 1 9 ( 2 α 1 + 2 α 2 − α 3 , 2 α 1 − α 2 + 2 α 3 ) = 1 9 ( 4 − 2 − 2 ) = 0 \begin{array}{l} \left(\beta_{1}, \beta_{1}\right)=\frac{1}{9}\left(2 \alpha_{1}+2 \alpha_{2}-\alpha_{3}, 2 \alpha_{1}+2 \alpha_{2}-\alpha_{3}\right)=\frac{1}{9}(4+4+1)=1 \\ \left(\beta_{1}, \beta_{2}\right)=\frac{1}{9}\left(2 \alpha_{1}+2 \alpha_{2}-\alpha_{3}, 2 \alpha_{1}-\alpha_{2}+2 \alpha_{3}\right)=\frac{1}{9}(4-2-2)=0 \end{array} (β1,β1)=91(2α1+2α2−α3,2α1+2α2−α3)=91(4+4+1)=1(β1,β2)=91(2α1+2α2−α3,2α1−α2+2α3)=91(4−2−2)=0
同理可计算得 : ( β 1 , β 3 ) = ( β 2 , β 3 ) = 0 , ( β 2 , β 2 ) = ( β 3 , β 3 ) = 1 , … :\left(\beta_{1}, \beta_{3}\right)=\left(\beta_{2}, \beta_{3}\right)=0,\left(\beta_{2}, \beta_{2}\right)=\left(\beta_{3}, \beta_{3}\right)=1, \ldots :(β1,β3)=(β2,β3)=0,(β2,β2)=(β3,β3)=1,…
方法 2 : 2: 2: 证明 B T B = I \boldsymbol{B}^{T} \boldsymbol{B}=\boldsymbol{I} BTB=I 即可:
B = ( β 1 , β 2 , β 3 ) = 1 3 ( α 1 , α 2 , α 3 ) ⏟ A ( 2 2 1 2 − 1 − 2 − 1 2 − 2 ) ⏟ C = 1 3 A C B T B = 1 9 ( A C ) T ( A C ) = 1 9 C T A T A C = 1 9 C T C = I ⇒ B 正交. \begin{array}{l} B=\left(\beta_{1}, \beta_{2}, \beta_{3}\right)=\frac{1}{3} \underbrace{\left(\alpha_{1}, \alpha_{2}, \alpha_{3}\right)}_{A} \underbrace{\left(\begin{array}{ccc} 2 & 2 & 1 \\ 2 & -1 & -2 \\ -1 & 2 & -2 \end{array}\right)}_{C}=\frac{1}{3} A C \\ B^{T} B=\frac{1}{9}(A C)^{T}(A C)=\frac{1}{9} C^{T} A^{T} A C=\frac{1}{9} C^{T} C=I \quad \Rightarrow B \text { 正交. } \end{array} B=(β1,β2,β3)=31A (α1,α2,α3)C ⎝⎛22−12−121−2−2⎠⎞=31ACBTB=91(AC)T(AC)=91CTATAC=91CTC=I⇒B 正交.
例 2 \Large{\color{violet}{例2}} 例2. 设 A = ( a i j ) 3 × 3 A=\left(a_{i j}\right)_{3 \times 3} A=(aij)3×3 是 3 阶正交矩阵, a 11 = 1 , b = ( 1 , 0 , 0 ) T a_{11}=1, b=(1,0,0)^{T} a11=1,b=(1,0,0)T, 求线性方程组 A X = b A X=b AX=b 的解.
证明:
a 11 = 1 a 11 2 + a 12 2 + a 13 2 = 1 a 11 2 + a 21 2 + a 31 2 = 1 } ⇒ a 12 = a 13 = a 21 = a 31 = 0 ⇒ A X = b : ( 1 0 0 0 a 22 a 23 0 a 32 a 33 ) ( x 1 x 2 x 3 ) = ( 1 0 0 ) 有解 ( 1 0 0 ) A 正交 ⇒ A 可逆 ⇒ A X = b 有唯一解 ⇒ X = ( 1 0 0 ) . \left.\begin{array}{l}\text { } \quad a_{11}=1 \\ a_{11}^{2}+a_{12}^{2}+a_{13}^{2}=1 \\ a_{11}^{2}+a_{21}^{2}+a_{31}^{2}=1\end{array}\right\} \Rightarrow a_{12}=a_{13}=a_{21}=a_{31}=0\\ \begin{array}{l} \Rightarrow A X=b:\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right)\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) \text { 有解 }\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) \\ A \text { 正交 } \Rightarrow A \text { 可逆 } \Rightarrow A X=b \text { 有唯一解 } \Rightarrow X=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) . \end{array} a11=1a112+a122+a132=1a112+a212+a312=1⎭⎬⎫⇒a12=a13=a21=a31=0⇒AX=b:⎝⎛1000a22a320a23a33⎠⎞⎝⎛x1x2x3⎠⎞=⎝⎛100⎠⎞ 有解 ⎝⎛100⎠⎞A 正交 ⇒A 可逆 ⇒AX=b 有唯一解 ⇒X=⎝⎛100⎠⎞.
例 3 \Large{\color{violet}{例3}} 例3. ( 1 ) λ ∈ C \quad(1) \lambda \in \mathbb{C} (1)λ∈C 是正交矩阵 A A A 的特征值 ⇒ ∣ λ ∣ = 1. \Rightarrow|\lambda|=1 . ⇒∣λ∣=1.
( 2 ) (2) (2) 实数 λ ∈ R \lambda \in \mathbb{R} λ∈R 是正交矩阵 A A A 的特征值 ⇒ λ = ± 1. \Rightarrow \lambda=\pm 1 . ⇒λ=±1.
证明: ( 1 ) (1) (1) 设 α ∈ C n \alpha \in \mathbb{C}^{n} α∈Cn 是特征值 λ ∈ C \lambda \in \mathbb{C} λ∈C 的一个特征向量,则
A α = λ α ⇒ λ α ‾ T = A α ‾ T A \alpha=\lambda \alpha \Rightarrow \overline{\lambda \alpha}^{T}=\overline{A \alpha}^{T} \quad Aα=λα⇒λαT=AαT 同取共轭转置,注意到 A ˉ = A \bar{A}=A Aˉ=A
⇒ λ ˉ α − T = ( A α ˉ ) T = α ˉ T A T 右乘 A α ⇒ λ ˉ α ˉ T A α = α ˉ T A T A α A α = λ α , A T A = I ⇒ ( λ λ ˉ ) α ˉ − T α = α ˉ T α α ≠ 0 ⇒ α ˉ T α ≠ 0 ⇒ ∣ λ ∣ 2 = λ λ ˉ = 1 ⇒ ∣ λ ∣ = 1 λ λ ˉ = ∣ λ ∣ 2 \begin{array}{ll}\Rightarrow \bar{\lambda} \alpha^{-T}=(A \bar{\alpha})^{T}=\bar{\alpha}^{T} A^{T} & \text { 右乘 } A \alpha \\ \Rightarrow \bar{\lambda} \bar{\alpha}^{T} A \alpha=\bar{\alpha}^{T} A^{T} A \alpha & A \alpha=\lambda \alpha, A^{T} A=I \\ \Rightarrow(\lambda \bar{\lambda}) \bar{\alpha}^{-T} \alpha=\bar{\alpha}^{T} \alpha & \alpha \neq 0 \Rightarrow \bar{\alpha}^{T} \alpha \neq 0 \\ \Rightarrow|\lambda|^{2}=\lambda \bar{\lambda}=1 \Rightarrow|\lambda|=1 & \lambda \bar{\lambda}=|\lambda|^{2}\end{array} ⇒λˉα−T=(Aαˉ)T=αˉTAT⇒λˉαˉTAα=αˉTATAα⇒(λλˉ)αˉ−Tα=αˉTα⇒∣λ∣2=λλˉ=1⇒∣λ∣=1 右乘 AαAα=λα,ATA=Iα=0⇒αˉTα=0λλˉ=∣λ∣2
(2) 由(1)知 ∣ λ ∣ = 1 |\lambda|=1 ∣λ∣=1, 再由 λ ∈ R \lambda \in \mathbb{R} λ∈R 知 λ = ± 1 \lambda=\pm 1 λ=±1.
例 4 \Large{\color{violet}{例4}} 例4. 设 A A A 是奇数阶正交矩阵且 d e t A = 1. det~~A=~~1 . det A= 1. 则 1 是 A A A 的特征值.
分析: A \quad A A 正交 ⇒ A T A = I ∣ I − A ∣ = 0 \Rightarrow A^{T} A=I \quad|I-A|=0 ⇒ATA=I∣I−A∣=0 ?
∣ I − A ∣ = ∣ A T A − A ∣ = ∣ ( A T − I ) A ∣ = ∣ A T − I ∣ ⋅ ∣ A ∣ = ∣ A T − I T ∣ = ∣ ( A − I ) T ∣ = ∣ A − I ∣ = ( − 1 ) n ∣ I − A ∣ = − ∣ I − A ∣ ⇒ ∣ I − A ∣ = 0 \begin{aligned} |I-A| &=\left|A^{T} A-A\right|=\left|\left(A^{T}-I\right) A\right| &=\left|A^{T}-I\right| \cdot|A| \\ &=\left|A^{T}-I^{T}\right| \quad=\left|(A-I)^{T}\right| \quad &=|A-I| \\ &=(-1)^{n}|I-A|=-|I-A| \quad & \Rightarrow|I-A|=0 \end{aligned} ∣I−A∣=∣∣ATA−A∣∣=∣∣(AT−I)A∣∣=∣∣AT−IT∣∣=∣∣(A−I)T∣∣=(−1)n∣I−A∣=−∣I−A∣=∣∣AT−I∣∣⋅∣A∣=∣A−I∣⇒∣I−A∣=0
所以 1 是 A A A 的特征值.
类似可证: 行列式为ー1的正交矩阵, 必有特征值 -1.
定理5. A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n 可逆 ⇒ \Rightarrow ⇒ 存在正交矩阵 Q Q Q 与正线上三角矩阵 R R R 使得 A = Q R A=Q R A=QR.
欧氏空间上的同构
定义: 设 V 1 , V 2 V_{1}, V_{2} V1,V2 都是欧氏空间,若 A : V 1 → V 2 \mathcal{A}: V_{1} \rightarrow V_{2} A:V1→V2 满足:
(1) A \mathcal{A} A 是线性同构;
(2) ( A α , A β ) = ( α , β ) , ∀ α , β ∈ V (\mathcal{A} \alpha, \mathcal{A} \beta)=(\alpha, \beta), \forall \alpha, \beta \in V (Aα,Aβ)=(α,β),∀α,β∈V.
则称 A \mathcal{A} A 是从欧氏空间 V 1 V_{1} V1 到 V 2 V_{2} V2 的同构. \quad 即 : : : 双射 +保持线性运算+保持内积
注记:
- [1]同构欧氏空间都是同构线性空间,维数必然相同;
- [2] 欧氏空间之间的同构映射比线性同构的要求更高!
定理6. V V V 是 n n n 维欧氏空间 ⇒ V \Rightarrow V ⇒V 与 R n ( \mathbb{R}^{n}( Rn( 关于标准内积)作为欧氏空间是同构的.
证明:任取 V V V 的一组标准正交基 α 1 , ⋯ , α n \alpha_{1}, \cdots, \alpha_{n} α1,⋯,αn, 规定映射:
A : V → R n , A α i = ε i ( 1 ≤ i ≤ n ) \mathcal{A}: V \rightarrow \mathbb{R}^{n}, \mathcal{A} \alpha_{i}=\varepsilon_{i}(1 \leq i \leq n) A:V→Rn,Aαi=εi(1≤i≤n)
由定理 知, A \mathcal{A} A 是线性映射,且 A \mathcal{A} A 显然是双射 ⇒ A \Rightarrow \mathcal{A} ⇒A 是线性同构.
A \mathcal{A} A 保持内积: ∀ α = x 1 α 1 + ⋯ + x n α n , β = y 1 α 1 + ⋯ + y n α n \quad \forall \alpha=x_{1} \alpha_{1}+\cdots+x_{n} \alpha_{n}, \beta=y_{1} \alpha_{1}+\cdots+y_{n} \alpha_{n} ∀α=x1α1+⋯+xnαn,β=y1α1+⋯+ynαn
A α = x 1 ε 1 + ⋯ + x n ε n = ( x 1 , ⋯ , x n ) , A β = ( y 1 , ⋯ , y n ) \mathcal{A} \alpha=x_{1} \varepsilon_{1}+\cdots+x_{n} \varepsilon_{n}=\left(x_{1}, \cdots, x_{n}\right), \mathcal{A} \beta=\left(y_{1}, \cdots, y_{n}\right) Aα=x1ε1+⋯+xnεn=(x1,⋯,xn),Aβ=(y1,⋯,yn)
( α , β ) = x 1 y 1 + ⋯ + x n y n = ( A α , A β ) ⇒ A (\alpha, \beta)=x_{1} y_{1}+\cdots+x_{n} y_{n}=(\mathcal{A} \alpha, \mathcal{A} \beta) \Rightarrow \mathcal{A} (α,β)=x1y1+⋯+xnyn=(Aα,Aβ)⇒A 是欧氏空间的同构映射.
定理7. 设 V 1 , V 2 V_{1}, V_{2} V1,V2 是有限维欧氏空间,则 V 1 , V 2 V_{1}, V_{2} V1,V2 是同构的欧氏空间 ⇔ dim V 1 = dim V 2 . \Leftrightarrow \operatorname{dim} V_{1}=\operatorname{dim} V_{2} . ⇔dimV1=dimV2.
注记:(1) 欧氏同构映射必为线性同构映射.
(2) 线性同构映射, 未必是欧氏同构映射:
V 1 = { ( a , b ) ∣ a , b ∈ R } , V 2 = { ( x y ) ∣ x , y ∈ R } V_{1}=\{(a, b) \mid a, b \in \mathbb{R}\}, V_{2}=\left\{\left(\begin{array}{l} x \\ y \end{array}\right) \mid x, y \in \mathbb{R}\right\} V1={ (a,b)∣a,b∈R},V2={ (xy)∣x,y∈R}
A : ( a , b ) ↦ ( a b ) \mathcal{A}:(\boldsymbol{a}, \boldsymbol{b}) \mapsto\left(\begin{array}{l}\boldsymbol{a} \\ \boldsymbol{b}\end{array}\right) A:(a,b)↦(ab) 是欧氏同构映射.
B : ( a , b ) ↦ ( a 2 b ) \mathcal{B}:(\boldsymbol{a}, \boldsymbol{b}) \mapsto\left(\begin{array}{c}\boldsymbol{a} \\ \mathbf{2 b}\end{array}\right) B:(a,b)↦(a2b) 是线性同构映射, 但不是欧氏同构映射.
参考
高等代数 电子科技大学