传染病预测模型:SI、SIS、SIR、SEIR、SEIAR
一、SI模型
1.1 定义
| 符号 | 名称 |
|---|---|
| S:Susceptible | 易感者 |
| I:Infectious | 感染者 |
设置参数:
| 参数 | 意义 |
|---|---|
| N | 总人数 |
| S | 易感人数 |
| I | 患病人数(感染者) |
| r | 感染者每天碰到的人数 |
| b | 传染率 |
-
那么有,S和I每天的变化人数为:
delta_s(t) = - I(t) * b * r * S(t)/N
delta_i(t) = I(t) * b * r * S(t)/N
-
第t天,S和I的人数为:
S(t) = S(t-1) + delta_s(t-1)
I(t) = I(t-1) + delta_i(t-1)
1.2 代码
import matplotlib.pyplot as plt
N = 10000 # 总人数
I = [1] # 患病人数
S = [N - 1] # 易感人数
r = 10 # 患病者每天要碰到的人数
B = 0.01 # 传染率
T = 200
for _ in range(1, T):
delta_s = - r * B * I[-1] * S[-1] / N
delta_i = r * B * I[-1] * S[-1] / N
S.append(S[-1] + delta_s)
I.append(I[-1] + delta_i)
plt.plot(range(T), S, 'blue', range(T), I, 'red')
plt.xlabel('day')
plt.ylabel('person')
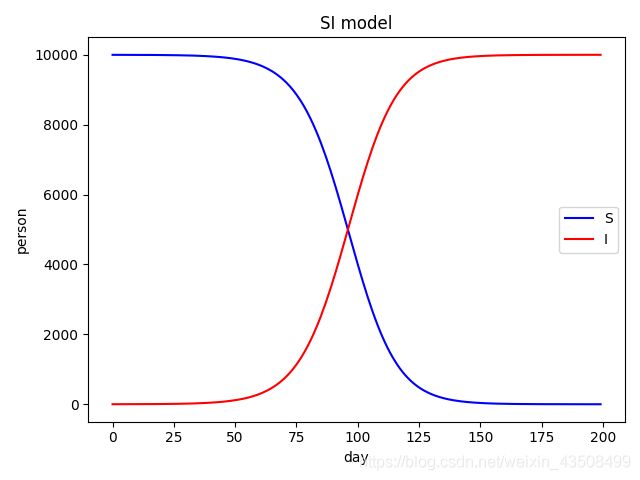
plt.title('SI model')
plt.legend(['S', 'I'])
plt.show()
二、SIS模型
2.1 定义
| 符号 | 名称 |
|---|---|
| S:Susceptible | 易感者 |
| I:Infectious | 感染者 |
| S:Susceptible | 易感者 |
SIS:引入感染者康复的概率,感染者还会转变成易感者,S -> I -> S。
设置参数:
| 参数 | 意义 |
|---|---|
| N | 总人数 |
| S | 易感人数 |
| I | 患病人数(感染者) |
| r | 感染者每天碰到的人数 |
| b | 传染率 |
| y(新引入) | 感染者康复的概率 |
-
那么有,S和I每天的变化人数为:
delta_s(t) = - I(t) * b * r * S(t)/N + y * I(t)
delta_i(t) = I(t) * b * r * S(t)/N - y * I(t)
-
第t天,S和I的人数为:
S(t) = S(t-1) + delta_s(t - 1)
I(t) = I(t-1) + delta_i(t - 1)
2.2 代码
import matplotlib.pyplot as plt
N = 10000 # 总人数
I = [1] # 患病人数
S = [N - 1] # 易感人数
r = 10 # 患病者每天要碰到的人数
B = 0.01 # 传染率
y = 0.02 # 感染者康复的概率
T = 200
for _ in range(1, T):
delta_s = - r * B * I[-1] * S[-1] / N + y*I[-1]
delta_i = r * B * I[-1] * S[-1] / N - y*I[-1]
S.append(S[-1] + delta_s)
I.append(I[-1] + delta_i)
plt.plot(range(T), S, 'blue', range(T), I, 'red')
plt.xlabel('day')
plt.ylabel('person')
plt.title('SIS model')
plt.legend(['S', 'I'])
plt.show()
跑出来的结果如下图所示:
三、SIR模型
3.1 定义
| 符号 | 名称 |
|---|---|
| S:Susceptible | 易感者 |
| I:Infectious | 感染者 |
| R:Recovered | 康复者 |
SIR模型,引入了康复者。
相比与SIS模型,SIR模型就是把y*I[-1]这一项单独设置为康复者。
设置参数:
| 参数 | 意义 |
|---|---|
| N | 总人数 |
| S | 易感人数 |
| I | 患病人数(感染者) |
| R(新引入) | 康复者人数 |
| r | 感染者每天碰到的人数 |
| b | 传染率 |
| y | 感染者康复的概率 |
-
那么有,S、I和R每天的变化人数为:
delta_s(t) = - I(t) * b * r * S(t)/N
delta_i(t) = I(t) * b * r * S(t)/N - y * I(t)
delta_r(t) = y * I(t)
-
第t天,S、I和R的人数为:
S(t) = S(t-1) + delta_s(t - 1)
I(t) = I(t-1) + delta_i(t - 1)
R(t) = R(t-1) + delta_r(t - 1)
3.2 代码
import matplotlib.pyplot as plt
N = 10000 # 总人数
I = [1] # 患病人数
S = [N - 1] # 易感人数
R = [0] # 康复人数(康复之后产生抗体,不再感染)
r = 10 # 患病者每天要碰到的人数
B = 0.05 # 传染率
y = 0.1 # 感染者康复的概率
T = 100
for i in range(1, T):
delta_s = - r * B * I[-1] * S[-1] / N
delta_i = r * B * I[-1] * S[-1] / N - y * I[-1]
delta_r = y*I[-1]
S.append(S[-1] + delta_s)
I.append(I[-1] + delta_i)
R.append(R[-1] + delta_r)
plt.plot(range(T), S, 'blue', range(T), I, 'red', range(T), R, 'green')
plt.xlabel('day')
plt.ylabel('person')
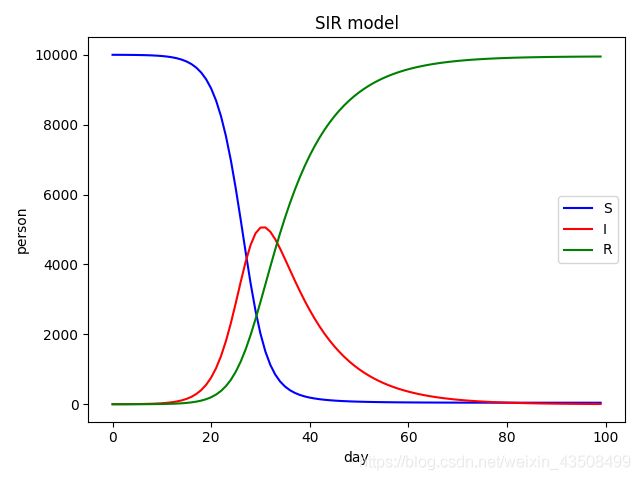
plt.title('SIR model')
plt.legend(['S', 'I', 'R'])
plt.show()
四、SEIR模型
4.1 定义
| 符号 | 名称 |
|---|---|
| S:Susceptible | 易感者 |
| E:Exposed | 潜伏者 |
| I:Infectious | 感染者 |
| R:Recovered | 康复者 |
SEIR模型引入了潜伏者E,潜伏者会转变为感染者。
在SEIR模型中,S会先变为E,E再变为I,I康复变成R。
S -> E -> I -> R
设置参数:
| 参数 | 意义 |
|---|---|
| N | 总人数 |
| S | 易感人数 |
| E(新引入) | 潜伏者人数 |
| I | 患病人数(感染者) |
| R | 康复者人数 |
| r | 感染者每天碰到的人数 |
| b | 传染率 |
| y | 感染者康复的概率 |
| a(新引入) | 潜伏者转化为感染者的概率 |
-
那么有,S、E、I和R每天的变化人数为:
delta_s(t) = - I(t) * b * r * S(t)/N
delta_e(t) = I(t) * b * r * S(t)/N - a * E(t)
delta_i(t) = a * E(t) - y * I(t)
delta_r(t) = y * I(t)
-
第t天,S、E、I和R的人数为:
S(t) = S(t-1) + delta_s(t - 1)
E(t) = E(t-1) + delta_e(t - 1)
I(t) = I(t-1) + delta_i(t - 1)
R(t) = R(t-1) + delta_r(t - 1)
4.2 代码
import matplotlib.pyplot as plt
N = 10000 # 总人数
E = [0] # 潜伏人数
I = [1] # 患病人数
S = [N - 1] # 易感人数
R = [0] # 康复人数(康复之后产生抗体,不再感染)
r = 20 # 患病者每天要碰到的人数
B = 0.03 # 传染率
a = 0.1 # 潜伏者转化为感染者的概率
y = 0.1 # 感染者康复的概率
T = 150
for i in range(1, T):
delta_s = - r * B * I[-1] * S[-1] / N
delta_e = r * B * I[-1] * S[-1] / N - a*E[-1]
delta_i = a*E[-1] - y*I[-1]
delta_r = y * I[-1]
S.append(S[-1] + delta_s)
E.append(E[-1] + delta_e)
I.append(I[-1] + delta_i)
R.append(R[-1] + delta_r)
plt.plot(range(T), S, 'blue', range(T), E, 'orange', range(T), I, 'red', range(T), R, 'green')
plt.xlabel('day')
plt.ylabel('person')
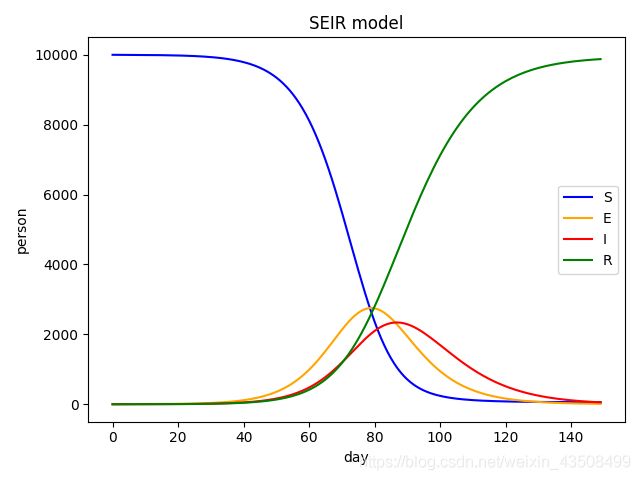
plt.title('SEIR model')
plt.legend(['S', 'E', 'I', 'R'])
plt.show()
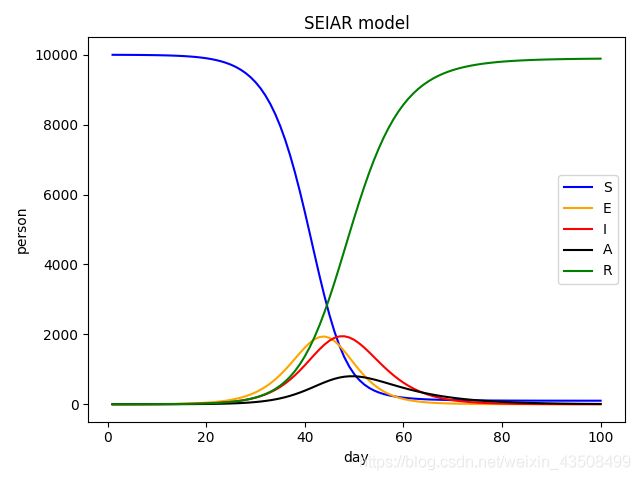
跑出来的结果如下图所示:
五、SEIAR模型
这个模型主要参考论文:《SEIAR 传染病动力学模型的建立及实现》
5.1 定义
| 符号 | 名称 |
|---|---|
| S:Susceptible | 易感者 |
| E:Exposed | 潜伏者 |
| I:Infectious | 感染者(显性感染者) |
| A:Asymptomatic | 无症状感染者(隐性感染者) |
| R:Recovered | 康复者 |
SEIAR模型,引入了无症状感染者A,把SEIR模型中的I进一步分为I和A。
(这里不再设置每天遇到的人数)
参数设置如下:
| 参数 | 意义 |
|---|---|
| N | 总人数 |
| S | 易感人数 |
| E | 潜伏者人数 |
| I | 有症状感染者人数(显性感染者) |
| A | 无症状感染者人数(隐性感染者) |
| R | 康复者人数 |
| b | 传染率 |
| k | 隐性感染者相对显性感染者的相对倍数(0<= k <=1) |
| w | 易感者变为显性感染者的速率(等于 潜伏期的倒数)(S(E) -> I) |
| w1 | 易感者变为隐性感染者的速率(等于 潜隐期的倒数)(S (E)- > A) |
| g | 显性感染者变为康复者的速率 (I -> R) |
| g1 | 隐性感染者变为康复者的速率 (A -> R) |
| p | 隐性症状感染者的比例 |
-
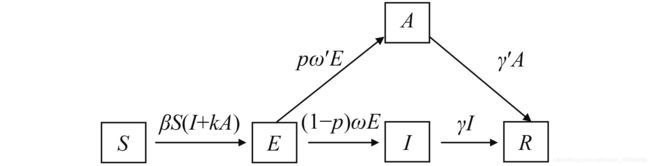
那么有,S、E、I、A和R每天的变化人数为(这里是参照原文给的公式写的):
delta_s(t) = - I(t) * b * S(t) - A(t) * b * k * S(t)
delta_e(t) = I(t) * b * S(t) + A(t) * b * k * S(t) - (1 - p) * w * E(t) - p * w1 * E(t)
delta_i(t) = (1 - p) * w * E(t) - g * I(t)
delta_a(t) = p * w1 * E(t) - g1 * A(t)
delta_r(t) = g * I(t) + g1 * A(t)
-
第t天,S、E、I、A和R的人数为:
S(t) = S(t-1) + delta_s(t - 1)
E(t) = E(t-1) + delta_e(t - 1)
I(t) = I(t-1) + delta_i(t - 1)
A(t) = A(t - 1) + delta_a(t - 1)
R(t) = R(t-1) + delta_r(t - 1)
5.2 代码
start_time = 1
stop_time = 100
dt = 1
# 参数设置
S = [10000] # 易感者
E = [0] # 潜伏者
I = [1] # 感染者
A = [0] # 无症状感染者
R = [0] # 恢复者
N = S[0] + I[0]
b = 0.8 # 易感者被传染的概率 S >> I
k = 0.7 # 无症状感染者(A)相对感染者(I)的传染力的倍数, S>>a
w = 1/3 # 易感者变为感染者的速率(潜伏期倒数) S >> I
w1 = 1/5 # 易感者变为隐性感染者的速率 S >> A
g = 1/5 # 显性感染者变为恢复者的速率,病程倒数 I >> R
g1 = 1/10 # 隐性感染者变为恢复者的速率 A >> R
p = 0.3 # 无症状感染者比例
# res_s, res_e, res_i, res_a, res_r = [S], [E], [I], [A], [R]
for i in range(start_time+1, start_time + stop_time):
delta_s = -b * S[-1] * I[-1]/N - b * S[-1] * k * A[-1]/N
delta_e = b * S[-1] * I[-1]/N + b * S[-1] * k * A[-1]/N - (1 - p) * w * E[-1] - p * w1 * E[-1]
delta_i = (1 - p) * w * E[-1] - I[-1] * g
delta_a = p * w1 * E[-1] - g1 * A[-1]
delta_r = I[-1] * g + g1 * A[-1]
# print(i, S[-1],delta_s, delta_e, delta_i, delta_a, delta_r)
# print(S[-1] + E[-1] + I[-1] + A[-1] + R[-1])
S.append(S[-1] + delta_s)
E.append(E[-1] + delta_e)
I.append(I[-1] + delta_i)
A.append(A[-1] + delta_a)
R.append(R[-1] + delta_r)
import matplotlib.pyplot as plt
time = list(range(start_time, start_time + stop_time))
plt.plot(time, S, 'blue', time, E, 'orange', time, I, 'red', time, A, 'black', time, R, 'green',)
# plt.plot(time, I, 'blue')
plt.xlabel('day')
plt.ylabel('person')
plt.title('SEIAR model')
plt.legend(['S', 'E', 'I', 'A', 'R'])
plt.show()
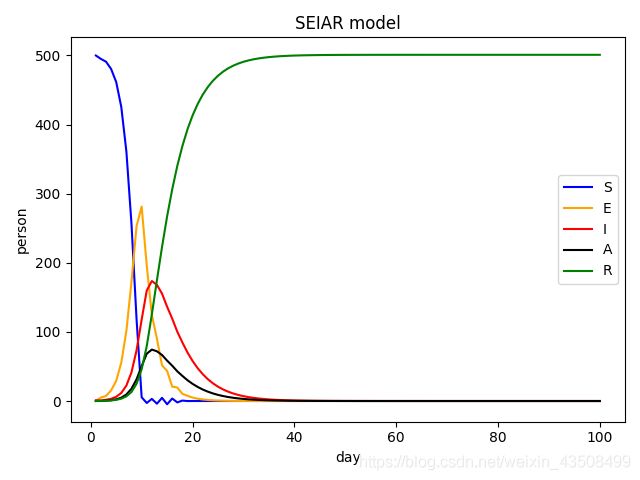
跑出来的结果如下所示:
5.3 关于SEIAR模型的疑问
相比于其他几种模型的微分方程,如SIR、SEIR等,他们的delta_s和delta_e中,都要除以N,什么意思呢,如下图所示:
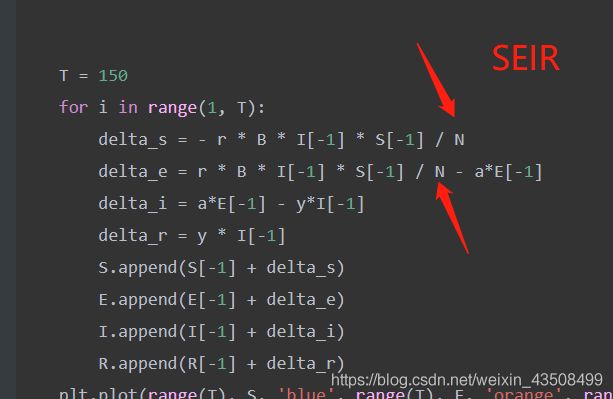
参考一些文章,如https://zhuanlan.zhihu.com/p/128986309?utm_source=wechat_session所说:

但是在SEIAR这边文章中,微分方程为:

跟N无关了,按照这种方法,会出现S变为负值的情况。例如设置S=500,传染率b=0.01,会出现如下图所示情况:
或者出现趋于无穷的情况。例如,设置S=500, b=0.1,会出现如下图所示情况:
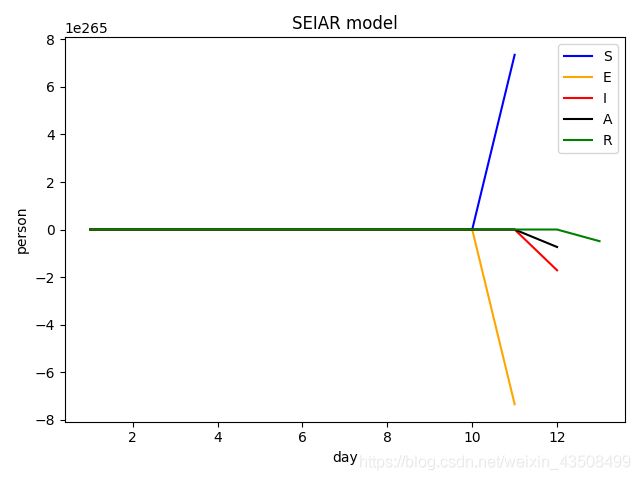
很明显,这种情况应该是不正确的,所以我在SEIAR部分的代码中,微分方程除以了N,这样得到的结果看上去是比较平滑合理的。
具体原因,后续还有待查证。
(2021.4.30更新)
看到维基百科上的一段:(https://en.wikipedia.org/wiki/File:SIR_model_anim.gif)

确实,这里的β 应该指的是β/N 的意思。破案了破案了!!!
总结下来:传染率还是要根据实际情况取值,否则画出来的曲线就没有意义了。
结束。