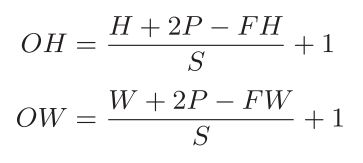都2021年了,不会还有人连深度学习不了解吧(二)- 卷积篇
一、前言
上篇文章详细阐述了激活函数是什么、常用的激活函数有哪些以及为什么要使用激活函数,相信大家对此有了一定的了解。在此基础上,我们趁热打铁,继续学习深度学习其它必须的知识。该篇文章讲述卷积操作及其它衍生出的操作,我愿称之为最强!卷积自提出以来,凭借其优异的提取特征的能力,已逐渐称为现代CNN网络中必不可少的组成部分,并引发了基于深度学习的方法研究计算机视觉的浪潮!
![]()
二、普通卷积
在阐述卷积的工作原理之前,我们需要了解一下为什么要使用卷积,以及卷积神经网络相较于全连接神经网络的优势体现在哪里。
2.1 全连接神经网络的缺陷
在未出现卷积神经网络之前,深度学习一直用的都是全连接神经网络,何为全连接,所谓的全连接即相邻层的所有神经元之前都有连接,无疑,这样做的参数量是巨大的。这是全连接神经网络存在的问题之一。然而这并不足以致命,最致命的问题在于全连接神经网络“ 忽视 ”了数据的形状。什么意思呢?看下面这个案例。
比如,输入数据是图像时,图像通常是高、长、通道方向上的3维形状。但是,向全连接层输入时,需要将3维数据拉平为1维数据。实际上,在MNIST数据集的例子中,输入图像就是1通道、高28像素、长28像素的(1, 28, 28)形状,但却被排成1列,以784个数据的形式输入到全连接神经网络中。
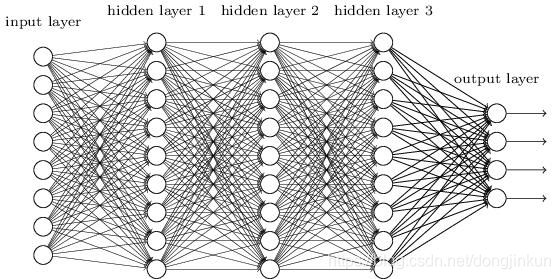
假设输入图像是3维形状,那么这个形状中应该含有重要的空间信息,否则没有必要是3维的。这些信息可能包含空间上邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式。但是,因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息。这是全连接神经网络最致命的问题。
2.2 卷积的工作原理
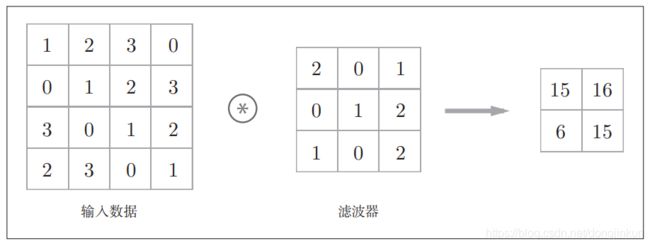
step1:
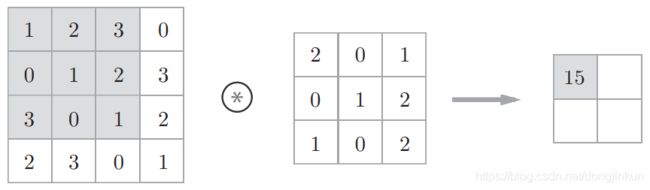
step2:
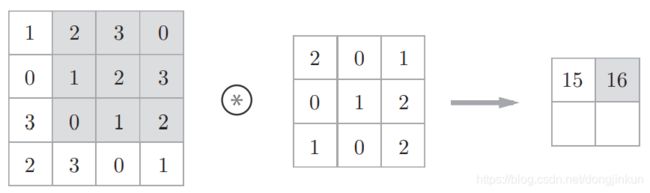
step3:
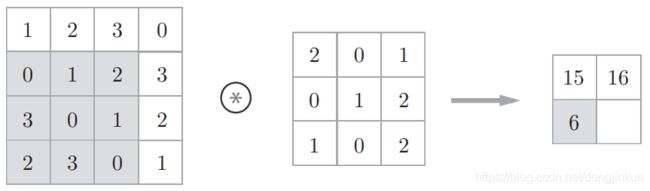
step4:
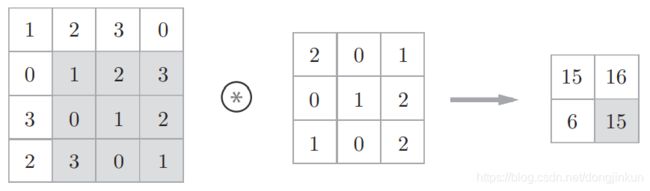
通过下面这2张图可以更加直观的理解卷积的工作原理。
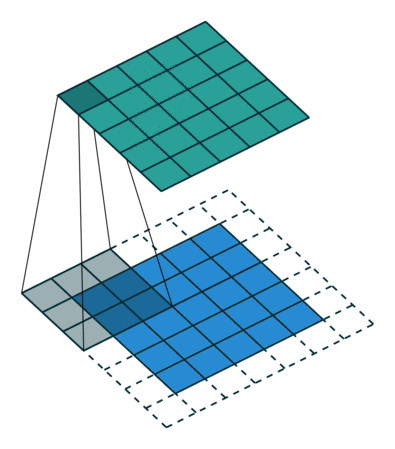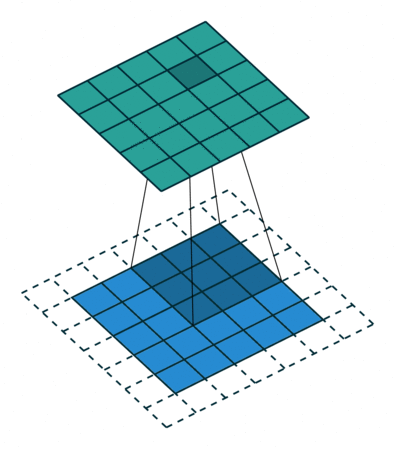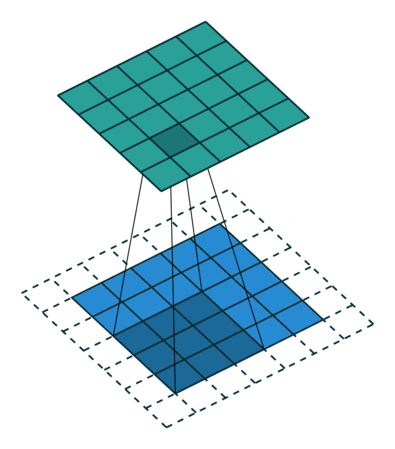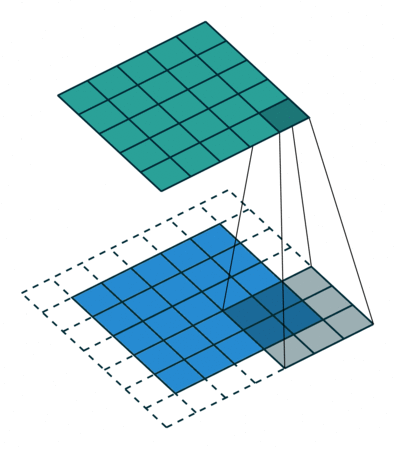
2.3 Output size如何计算
假设输入大小为(H, W),滤波器大小为(FH, FW),输出大小为(OH, OW),填充为P,步幅为S,输出大小可通过下式计算得到。
2.4 3维数据如何进行卷积
平时在做实验过程中,输入是有3个通道的RGB图像,这也是最常见的情形,所以需要阐述一下3维数据是如何进行卷积的,让我们一起看下面的案例,很简单但绝对经典:

step1:
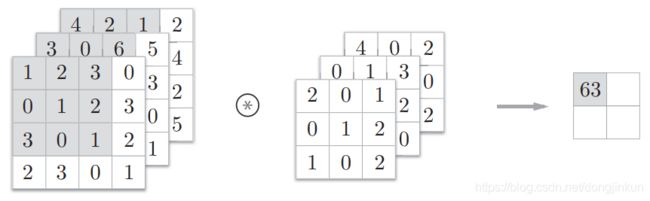
step2:
step3:
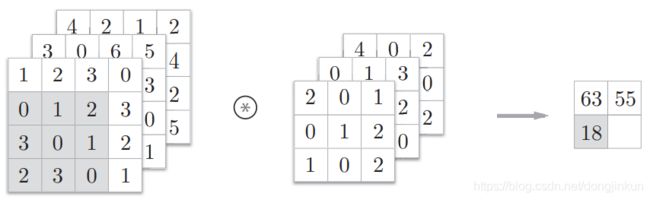
step4:
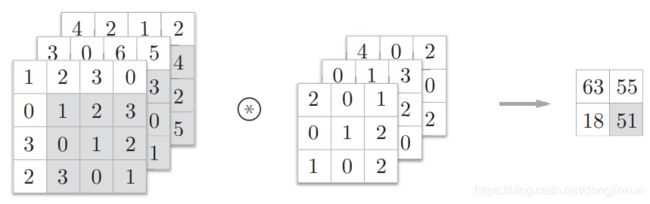
Note:值得注意的一点
在3维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值。在上面这个例子中,输入数据和滤波器的通道数一致,均为3。滤波器大小可以设定为任意值,不过,每个通道的滤波器大小要全部相同。
2.4 推荐论文
《Gradient-Based Learning Applied to Document Recognition》
《ImageNet Classification with Deep Convolutional Neural Networks》
三、空洞卷积
3.1 空洞卷积运行原理
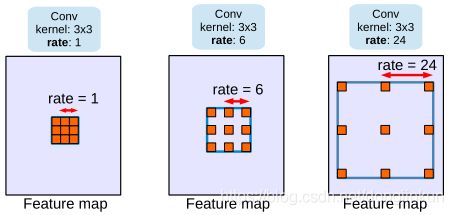
空洞卷积也被称为膨胀卷积。感受野是卷积神经网络中非常重要的概念,空洞卷积的目的就在于扩大感受野,以提升模型的性能。空洞卷积的运行原理跟卷积非常类似,唯一不同之处在于空洞卷积引入了一个**扩张率(dilated rate)**的概念,可以认为,普通卷积是空洞卷积的一种情形,普通卷积的扩张率默认为1。
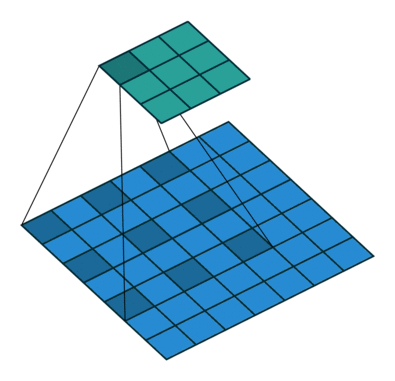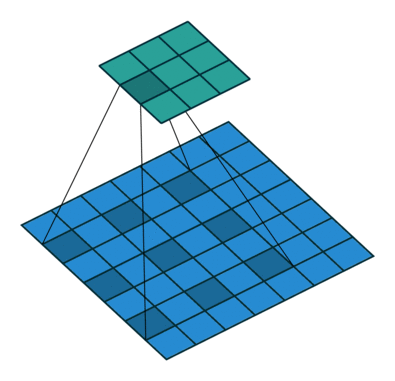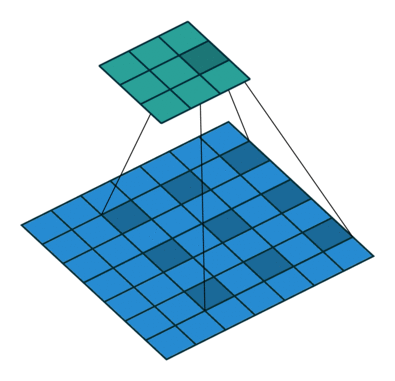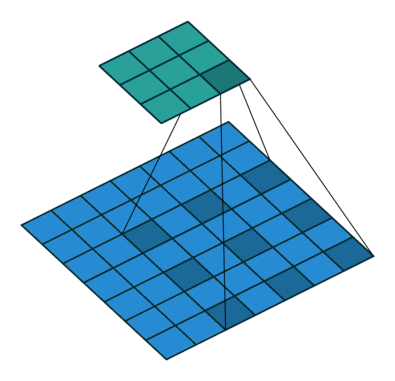
以下分别是dilated rate=1、dilated rate=6、dilated rate=24的空洞卷积案例:
3.2 推荐论文
关于空洞卷积的详细介绍可以查阅大名鼎鼎的DeepLab系列论文,以下分别是DeepLab v2和DeepLab v3。
《DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs》
《Rethinking Atrous Convolution for Semantic Image Segmentation》
四、转置卷积
转置卷积也被称为反卷积,顾名思义,转置卷积的操作与卷积操作是相反的,转置卷积常用于上采样阶段。什么是上采样,之后会有一篇文章专门来介绍常见的上采样方式,包括转置卷积、最近邻插值、双线性插值等等,由于转置卷积更偏向于上采样阶段,而该篇文章会更加偏向于提取特征的卷积方式,因此转置卷积会在之后的上采样篇进行详细阐述。
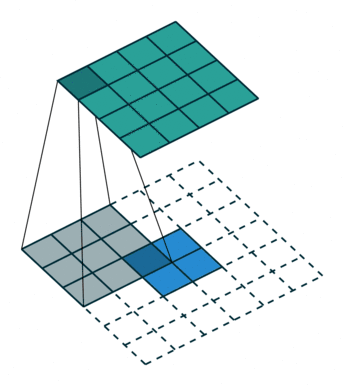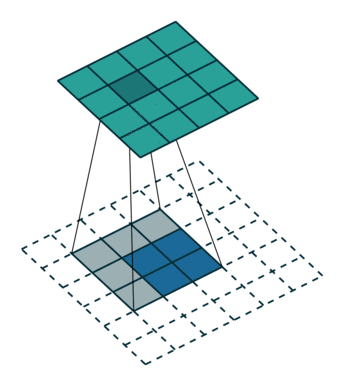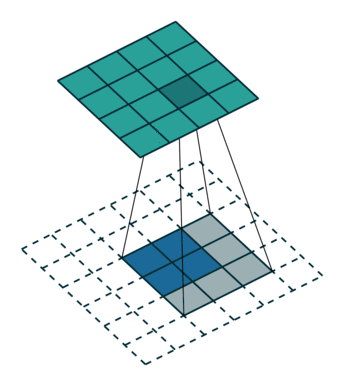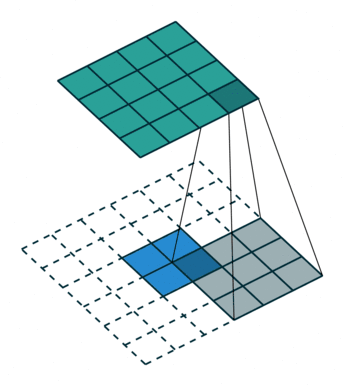
五、可分离卷积
可分离卷积分为空间可分离卷积和深度可分离卷积。
5.1 空间可分离卷积
空间可分离卷积是利用矩阵乘法的性质来设计的,具体请看以下的案例,假设卷积核size为33,那么这个卷积核可以看作是一个31的向量与1*3向量的乘法。这样做的好处在于减少了模型的参数,减少了乘法的计算量。
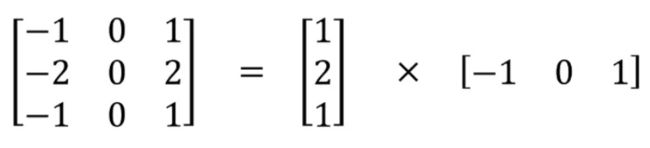
5.2 深度可分离卷积
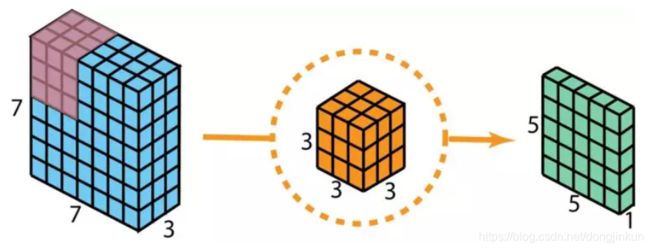
重点介绍深度可分离卷积,该卷积我愿称之为卷积神经网络中令人拍案叫绝的操作之一,深度可分离卷积分为2步,第1步是利用每个卷积核分别对输入图像的1个通道进行卷积,第2步是扩充深度,具体的运行原理如图(图来源)所示。
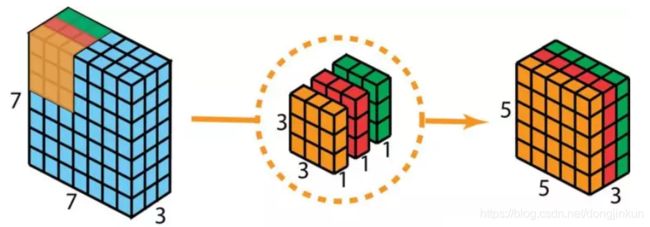
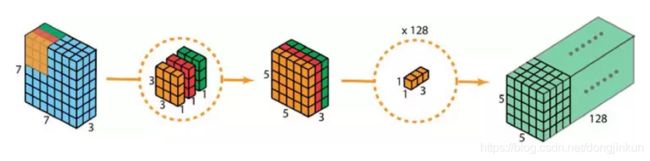
普通的卷积过程是使用与输入图像通道数相同的卷积核将输入图像输出为通道为1的特征图,而深度可分离卷积则是分别使用 3 个卷积核(每个卷积核的大小为 3 x 3 x 1),而不使用大小为 3 x 3 x 3 的卷积核,每个卷积核仅对输入图像的 1 个通道做卷积,这样的卷积每次都得出大小为 5 x 5 x 1 的映射,之后再将这些映射堆叠在一起创建一个 5 x 5 x 3 的图像,最终得出一个大小为 5 x 5 x 3 的输出图像。这样的话,图像的深度保持与原来的一样。
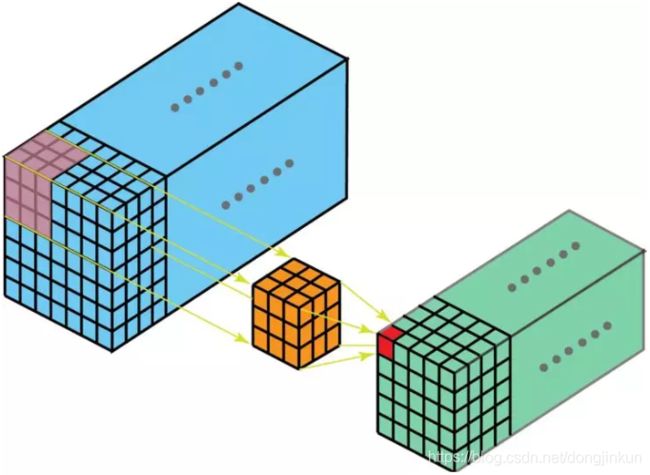
深度可分离卷积的第2步是扩充深度,我们用大小为 1x1x3 的卷积核做 1x1 卷积。每个 1x1x3 卷积核对 5 x 5 x 3 输入图像做卷积后都得出一个大小为 5 x 5 x1 的映射。
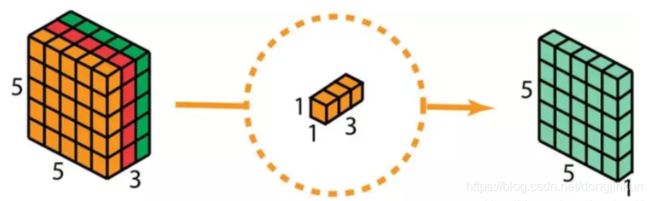
做 128 次 1x1 卷积后,就可以得出一个大小为 5 x 5 x 128 的特征图。
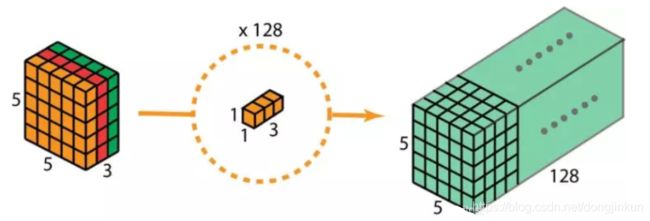
深度可分离卷积的完整过程如下图所示。
5.3 推荐论文
《Xception: Deep Learning with Depthwise Separable Convolutions》
六、3D卷积
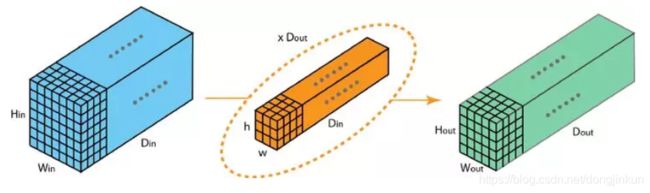
从名字中就可以明白3D卷积的大致意思了,普通卷积是在2维空间上进行卷积操作,3D卷积无非就是在3维空间上进行卷积操作。可以看到,3D卷积无非是2D卷积在通道维度上进行了扩展,3D 卷积核可以沿着 3 个方向移动(高、宽以及图像的通道),跟2D卷积并没有特别大的区别。如下图(图来源)所示:
七、分组卷积
7.1 分组卷积原理
分组卷积首次提出是在鼎鼎大名的AlexNet,详细了解AlexNet可以看我这篇博客AlexNet,非常详细,分组卷积的提出为了解决GPU算力不足的问题,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合。在普通卷积中,所有的卷积核一股脑的对输入图进行卷积。
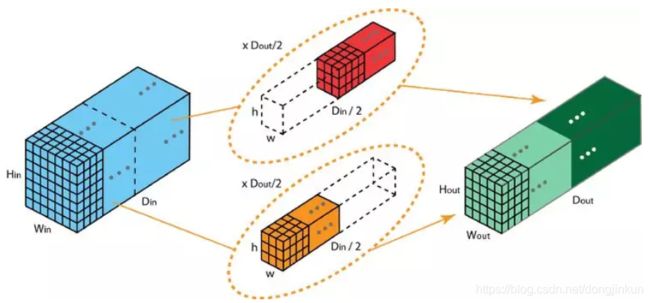
在分组卷积中,卷积核被拆分为不同的组,每一个组都负责具有一定深度的普通卷积的操作。下图(图来源)可以更为直观的表现分组卷积的运行原理。
7.2 推荐论文
推荐大家阅读下面这篇论文AlexNet,该篇论文可以称为是卷积神经网络的开山鼻祖之一,很经典。
《ImageNet Classification with Deep Convolutional Neural Networks》
参考文献
《深度学习入门-基于Python的理论与实现》
《ImageNet Classification with Deep ConvolutionalNeural Networks》
《Gradient-Based Learning Applied to Document Recognition》
《ImageNet Classification with Deep Convolutional Neural Networks》
https://blog.csdn.net/gwplovekimi/article/details/89890510
《Xception: Deep Learning with Depthwise Separable Convolutions》
计划 – 深度学习系列
都2021年了,不会还有人连深度学习还不了解吧?(一)-- 激活函数篇
都2021年了,不会还有人连深度学习还不了解吧?(二)-- 卷积篇
都2021年了,不会还有人连深度学习还不了解吧?(三)-- 损失函数篇
都2021年了,不会还有人连深度学习还不了解吧?(四)-- 上采样篇
都2021年了,不会还有人连深度学习还不了解吧?(五)-- 下采样篇
都2021年了,不会还有人连深度学习还不了解吧?(六)-- Padding篇
都2021年了,不会还有人连深度学习还不了解吧?(七)-- 评估指标篇
都2021年了,不会还有人连深度学习还不了解吧?(八)-- 优化算法篇
都2021年了,不会还有人连深度学习还不了解吧?(九)-- 注意力机制篇
都2021年了,不会还有人连深度学习还不了解吧?(十)-- 数据归一化篇