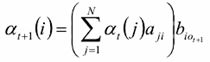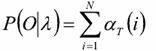七月算法-12月机器学习--第十七次课笔记-隐马尔科夫模型HMM
七月算法（julyedu.com）12月机器学习在线班学习笔记http://www.julyedu.com
隐马尔科夫模型
三个部分：概率计算，参数估计，模型预测
1，HMM定义
HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定。
Eg:以中文分词为例子
隐状态为
="2"，是不是终止字，是/否？（Y/N）即是不是最后一个字。
A矩阵：第一个：当前是终止字，下一个也是终止字的概率
B是当前的隐状态是终止词，观察到的终止字是什么,char
参数总结，隐状态是离散的，B是N*M矩阵，A是N*N的矩阵
1.2 HMM的两个基本性质
齐次假设：
观测独立性假设：
如果实践中，符合这两个性质，则可以考虑是否用HMM模型
Eg: 选一个盒子，摸一个放回
该示例的各个参数
1.3 HMM的3个基本问题
1，概率计算问题：前向-后向算法——动态规划
2, 学习问题：Baum-Welch算法(状态未知)——EM
3, 预测问题：Viterbi算法——动态规划
1.3.1 概率计算问题
三种方法，直接算法，前向算法，后向算法
1.3.2 直接算法
对所有可能的状态序列I求和，得到观测序列O的概率
直接算法，时间复杂度太高，只停留在理论阶段
1.3.3 前向算法
前向概率-后向概率的定义
前向算法
1，初值： 
2，递推：对于t=1,2…T-1
3，最终
前向算法的时间复杂度是o(T*
)
1.3.4 后向算法
1.3.5 前后向关系
在某一个时刻，
1.3.6 单个状态的概率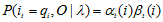
求给定模型λ和观测O，在时刻t处于状态qi的概率
最有可能发生的隐状态，取一个最大值
γ的意义：
不是Viterbi算法
1.3.7 两个状态的联合概率
求给定模型λ和观测O，在时刻t处于状态qi并且时刻t+1处于状态qj的概率。
1.4 HMM学习问题
1, 若训练数据包括观测序列和状态序列，则HMM的是监督学习；
2,若训练数据只有观测序列，则HMM的学习需要使用EM算法，是非监督学习。
1.4.1 Baum-Welch算法
本质上是EM算法
-
假设
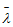是HMM参数的当前估计值，
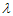为待求的参数。
-
EM过程
A, EM的STEP1先求联合概率
以上分成了3个部分，
B, EM的STEP2-期望极大值部分
1.5 HMM预测算法
两种算法：近似算法， Viterbi算法
1.5.1 Viterbi算法
Viterbi算法实际是用动态规划解HMM预测问题，用DP求概率最大的路径(最优路径)，这是一条路径对应一个状态序列。
定义变量
：在时刻t状态为i的所有路径中，概率的最大值。
总结：实践中分词的隐状态可以有多个，eg：开头，中间，最后一个等等