LeetCode题解-位运算
LeetCode题解-位运算
文章目录
- LeetCode题解-位运算
-
- 常用位运算符
- 基本原理
- 常用位操作
-
- 1.位与计算技巧
- 2.移位运算
- 3.mask计算
- 4.判断奇偶
- 5.不用额外变量交换两个整数
- 6. java中的位操作
- LeetCode题目
-
- 191.位1的个数(简单)
- 461.汉明距离(简单)
- 136.只出现一次的数字(简单)
- 260.只出现一次的数字 III(中等)
- 268.丢失的数字
- 190.颠倒二进制位(简单)
- 231. 2的幂(简单)
- 342. 4的幂(简单)
- 693.交替位二进制数(简单)
- 476.数字的补数(简单)
- 371.两整数之和(中等)
- 318.最大单词长度乘积(中等)
- 338.比特位计数(中等)
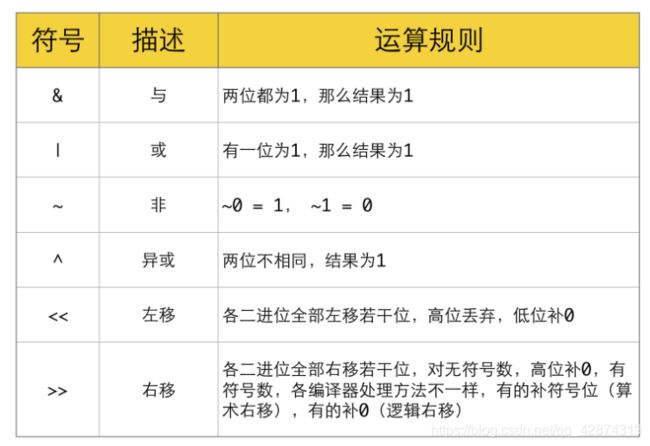
常用位运算符
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x //判断两个数是否相等(异或为0),两个数不相等(与为0);
利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
1^1^2 = 2
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
01011011 &
00111100
--------
00011000
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |
00111100
--------
01111111
常用位操作
1.位与计算技巧
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
01011011 &
01011010
--------
01011010
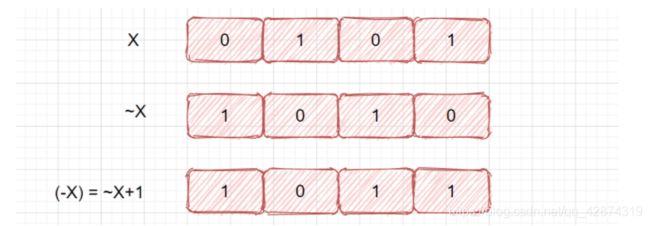
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n(补码)=~n(反码)+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &
01001100
--------
00000100
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
n & ~n -----> 0
2.移位运算
>> n 为算术右移,相当于除以 2n,例如 -7 >> 2 = -2。
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
>>> n 为无符号右移,左边会补上 0。例如 -7 >>> 2 = 1073741822。
11111111111111111111111111111001 >>> 2
--------
00111111111111111111111111111111
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
3.mask计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,(1< 要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1< 将 x 最右边的 n 位清零:x & (~0 << n) (x & 1) == 1 —等价—> (x % 2 == 1) 在计算机中,有符号数可分为原码、反码。补码 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。 背景小知识 **方法一:**通过 n & 1 来统计当前 n 的最低位是否为 1,同时每次直接对 n 进行右移并高位补 0。 方法二:使用 n & (n-1) 把 n 的二进制位中的最低位的 1 变为 0。不断让当前的 n 与 n - 1做与运算,直到 n 变为 0 即可。因为每次运算会使得 n的最低位的 1 被翻转,因此运算次数就等于 n 的二进制位中 1的个数。 **方法三:**直接利用函数Integer.bitCount() 来统计 1 个的个数 给出两个整数 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 **解题思路:**如果不考虑时间复杂度和空间复杂度的限制,可以使用集合或哈希表等方法,都需要额外使用 O(n) 的空间 如何才能做到线性时间复杂度和常数空间复杂度呢?注意题目中强调了重复的元素都是出现两次的,因此可以使用位运算。对于这道题,可使用异或运算 ⊕ ⊕ ⊕。异或运算有以下三个性质。 给定一个整数数组 **解题思路:**若是只有一个不重复的元素,则和上题一样,将所有元素进行异或,最后的值即为结果。但是在该题中有两个只出现一次的元素,那怎么将他们分别返回呢?考虑将所有数字分为两组,其满足: 两个只出现一次的元素被分到不同的组中; 相同的元素被分到相同的组中; 那么分别对两个组进行异或操作,则他们可以分别返回一个只出现一次的元素,那么结果即为这两个元素。 如何将这两个只出现一次的元素分到不同的组中,是这道问题的关键! 记这两个只出现了一次的数字为 a a a 和 b b b,那么所有数字异或的结果就等于 a a a和 b b b异或的结果,我们记为 x x x。将 x x x表示为二进制的形式,由于 a ≠ b a≠b a=b,则 x x x必定有一位为1,采用== d i f f = x diff =x diff=x& ( − x ) (-x) (−x)==的方式求出 x x x最右边的一个1,然后将它作为分组标准。 重新遍历数组,将每个数与diff进行&操作,依据结果为0或者1将他们分为两组,则每个组只有一个只出现一次的元素,然后再采用异或求出该元素即可。 [参考链接][https://leetcode-cn.com/problems/single-number-iii/solution/javawei-yun-suan-jie-jue-ji-bai-liao-999-dp5b/] 给定一个包含 进阶: **解题思路:方法一:**我们知道数组中有 n 个数,并且缺失的数在 [0…n] 中。因此我们可以先得到 [0…n] 的异或值,再将结果对数组中的每一个数进行一次异或运算。未缺失的数在 [0…n] 和数组中各出现一次,因此异或后得到 0。而缺失的数字只在[0…n] 中出现了一次,在数组中没有出现,因此最终的异或结果即为这个缺失的数字。 颠倒给定的 32 位无符号整数的二进制位。 方法一:逐位颠倒 将 n n n视为32位的二进制串,将 n n n不断右移,并采用== n n n&1==从低位到高位获取它的每一位,然后将其倒序添加到反转结果 r e s res res中 方法二:位运算分治(这个方法没看懂,后续再回来看) 给定一个整数,编写一个函数来判断它是否是 2 的幂次方。 **解题思路:**通过分析可知,判断一个整数是否是2的幂次方,即判断这个数的是否是大于零且二进制只有一位为1,那么问题就转化为怎么判断这个数的1的个数为1。我们可以采用上述191题的三种方法来统计1的个数,然后判断它是否为1即可。 给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 整数 **解题思路:**我们首先检查 给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同。 **解题思路:**考虑将n右移1位,如果n交替为0,则两者异或结果各位都为1;判断一个数是否全为1,可以将它加1,例如(0111,得到1000),然后进行&操作判断结果是否为0即可。 给你一个 正 整数 **解题思路:**首先想到,对0和1取反可以采用与1异或的方式,即 所以通过将num与二进制全为1的数(长度相等)异或,可以求出num的补数,例如对于 00000101,要求补码可以将它与 00000111 进行异或操作。那么问题就转换为求掩码 00000111。 要得到 1 到 i 位为 1 的 mask,只要在每次循环中使(0<<1) +1 即可。 不使用运算符 **解题思路:**先来观察下位运算中的两数加法,其实来来回回就只有下面这四种: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0(进位 1) 仔细一看,这可不就是相同位为 0,不同位为 1 的异或运算结果嘛~ 我们知道,在位运算操作中,异或的一个重要特性是无进位加法。我们来看一个例子: 由计算结果可见, 那么问题就容易了,总结一下: 1.a + b 的问题拆分为 (a 和 b 的无进位结果) + (a 和 b 的进位结果) 给定一个字符串数组 **解题思路:**本题的难点在于如何比较两个字符串是否含有重复的字母。 本题看中的是字符串中所包含字母的种类,而不是数量。因为单词仅包含小写字母,所以可以使用26 个字母的位掩码来对单词的每个字母处理,如果单词中存在字母 a,则将位掩码的第一位设为 1,否则设为 0。依次类推,一直判断到字母 总体思路: 遍历每个单词,然后去找序号比它大的单词是否不存在公共字母,无则计算是否是最大值。一直保存最大的即可 用位操作优化: 遍历单词的每个字母,计算该字母在掩码中的位置 n = (int)ch - (int)‘a’,然后创建一个第 n 位为 1 的掩码 n_th_bit = 1 << n,通过或操作将该码合并到位掩码中 bitmask |= n_th_bit。 预计算所有单词的位掩码,并把它们存储在数组 masks 中。使用数组 lens 存储所有单词的长度。 逐一两两比较单词。如果两个单词不存在公共字母,则更新最大单词长度乘积 maxProd。使用数组 masks 可以在常数时间内判断两个单词是否包含公共字母:(masks[i] & masks[j]) == 0 给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。 方法一:直接计算 方法二:动态规划(没看懂,回头再看) } 输入: 2 输入: 5 方法二:动态规划(没看懂,回头再看)
获取 x 的第 n 位值:(x >> n) & 1
获取 x 的第 n 位的幂值:x & (1 << n)
仅将第 n 位置为 1:x | (1 << n)
仅将第 n 位置为 0:x & (~(1 << n))
将 x 最高位至第 n 位(含)清零:x & ((1 << n) - 1)
将第 n 位至第 0 位(含)清零:x & (~((1 << (n + 1)) - 1))4.判断奇偶
(x & 1) == 0 —等价—> (x % 2 == 0)
x / 2 —等价—> x >> 15.不用额外变量交换两个整数
a = a ^ b;
b = a ^ b;
a = a ^ b;
6. java中的位操作
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串
LeetCode题目
191.位1的个数(简单)
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
public int hammingWeight(int n) {
int cnt = 0;
while(n != 0){
cnt += (n & 1);
n >>>= 1;
}
return cnt;
}
public int hammingWeight(int n) {
int cnt = 0;
while(n != 0){
n &= (n-1);
cnt++;
}
return cnt;
}
public int hammingWeight(int n) {
return Integer.bitCount(n);
}
461.汉明距离(简单)
x 和 y,计算它们之间的汉明距离。输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
public int hammingDistance(int x, int y) {
int z = x ^ y;
int cnt = 0;//对于统计1的个数,可以采用以上三种方法中任意一种
while(z != 0){
z &= (z - 1);
cnt++;
}
return cnt;
}
136.只出现一次的数字(简单)
输入: [2,2,1]
输出: 1
class Solution {
public int singleNumber(int[] nums) {
int ans = 0;
for(int num : nums) ans = ans ^ num;//两个相同的数异或的结果为 0,对所有数进行异或操作,最后的结果就是单独出现的那个数。
return ans;
}
}
260.只出现一次的数字 III(中等)
nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。输入:nums = [1,2,1,3,2,5]
输出:[3,5]
解释:[5, 3] 也是有效的答案。
class Solution {
public int[] singleNumber(int[] nums) {
int diff = 0;
for(int num : nums) diff ^= num;
diff &= (-diff);
int[] res = new int[2];
for(int num : nums){
//把数组分为两部分,每部分再分别异或
if((diff & num) == 0){
res[0] ^= num;
}else{
res[1] ^= num;
}
}
return res;
}
}
268.丢失的数字
[0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
class Solution {
public int missingNumber(int[] nums) {
int missing = nums.length;//数组索引为0~n-1,没有包含n,所以先假设丢失的数字为n
for(int i = 0; i < nums.length; i++){
missing = missing ^ i ^ nums[i];
}
return missing;
}
}
190.颠倒二进制位(简单)
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
public class Solution {
// you need treat n as an unsigned value
public int reverseBits(int n) {
int rev = 0;
for(int i = 0; i < 32 & n != 0; i++){
rev |= (n & 1) << (31 - i); //由于设定res各位为0,所以注意这里的或操作
n >>>= 1;
}
return rev;
}
}
public class Solution {
private static final int M1 = 0x55555555; // 01010101010101010101010101010101
private static final int M2 = 0x33333333; // 00110011001100110011001100110011
private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111
public int reverseBits(int n) {
n = n >>> 1 & M1 | (n & M1) << 1;
n = n >>> 2 & M2 | (n & M2) << 2;
n = n >>> 4 & M4 | (n & M4) << 4;
n = n >>> 8 & M8 | (n & M8) << 8;
return n >>> 16 | n << 16;
}
}
231. 2的幂(简单)
输入: 1
输出: true
解释: 20 = 1
输入: 16
输出: true
解释: 24 = 16
class Solution {
public boolean isPowerOfTwo(int n) {
return (n > 0) && ((n & (n - 1)) == 0);
}
}
public boolean isPowerOfTwo(int n) {
return n > 0 && Integer.bitCount(n) == 1;
}
342. 4的幂(简单)
true ;否则,返回 false 。n 是 4 的幂次方需满足:存在整数 x 使得 n == 4x输入:n = 16
输出:true
输入:n = 5
输出:false
n 是否为 2 的幂:n > 0 and n & (n - 1) == 0。再区分 2 的偶数幂(当 x 是 4 的幂时)和 2 的奇数幂(当 x 不是 4 的幂时),在第一种情况下(4 的幂),1 处于偶数位置:第 0 位、第 2 位、第 4 位等;在第二种情况下,1 处于奇数位置。class Solution {
public boolean isPowerOfFour(int n) {
return n > 0 && (n & (n - 1)) == 0 && (n & 0x55555555) != 0;//n的1位在偶数位(0101 0101 0101 0101,即十六进制5555)
}
}
693.交替位二进制数(简单)
输入:n = 5
输出:true
解释:5 的二进制表示是:101
输入:n = 7
输出:false
解释:7 的二进制表示是:111.
class Solution {
public boolean hasAlternatingBits(int n) {
int a = n ^ (n >> 1);
return (a & (a + 1)) == 0;
}
}
476.数字的补数(简单)
num ,输出它的补数。补数是对该数的二进制表示取反。输入:num = 5
输出:2
解释:5 的二进制表示为 101(没有前导零位),其补数为 010。所以你需要输出 2 。
输入:num = 1
输出:0
解释:1 的二进制表示为 1(没有前导零位),其补数为 0。所以你需要输出 0 。
class Solution {
public int findComplement(int num) {
int temp = num, c = 0;
while(temp > 0){
temp >>= 1;//每次循环右移一位,直至为0
c = (c << 1) + 1;
}
return num ^ c;
}
}
371.两整数之和(中等)
+ 和 - ,计算两整数 a 、b 之和。输入: a = 1, b = 2
输出: 3
输入: a = -2, b = 3
输出: 1
a = 5 = 0101 b = 4 = 0100
a ^ b 如下:
0 1 0 1
0 1 0 0
-------
0 0 0 1
a ^ b 得到了一个无进位加法结果,如果要得到 a + b 的最终值,我们还要找到进位的数,把这二者相加。在位运算中,我们可以使用与操作获得进位:a & b 如下:
0 1 0 1
0 1 0 0
-------
0 1 0 0
0100 并不是想要的进位,1 + 1 所获得的进位应该要放置在它的更高位, 因此我们还要把 0100 左移一位,才是我们所要的进位结果。
2.无进位加法使用异或运算计算得出
3.进位结果使用与运算和移位运算计算得出
4.循环此过程,直到进位为 0class Solution {
public int getSum(int a, int b) {
int sum, carry;
sum = a ^ b; //无进位加法
carry = (a & b) << 1; //进位
while(carry != 0){
//当进位不为0时,采用getSum递归求解sum与carry的和,直到进位为0;
return getSum(sum, carry);
}
return sum;
}
}
318.最大单词长度乘积(中等)
words,找到 length(word[i]) * length(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。输入: ["abcw","baz","foo","bar","xtfn","abcdef"]
输出: 16
解释: 这两个单词为 "abcw", "xtfn"。
输入: ["a","aa","aaa","aaaa"]
输出: 0
解释: 不存在这样的两个单词。
z。
class Solution {
public int maxProduct(String[] words) {
int n = words.length;
int[] mask = new int[n];//存放n个字符串的掩码
int[] len = new int[n];//存放n个字符串的长度
int bitmask;//每个字符串的掩码
for(int i = 0; i < n; i++){
bitmask = 0;
for(char c: words[i].toCharArray()){
bitmask |= 1 << (c - 'a');
}
mask[i] = bitmask;
len[i] = words[i].length();
}
int maxProd = 0;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
if((mask[i] & mask[j]) == 0){
maxProd = Math.max(ans, len[i] * len[j]);
}
}
}
return maxProd;
}
}
338.比特位计数(中等)
输入: 2
输出: [0,1,1]
输入: 5
输出: [0,1,1,2,1,2]
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i <= num; i++){
res[i] = Integer.bitCount(i); //从0~num计算每个数字包含的1的个数
}
return res;
}
}
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 1; i <= num; i++){
res[i] = res[i&(i-1)] + 1;
}
return res;
}
}
### 338.比特位计数(中等)
给定一个非负整数 **num**。对于 **0 ≤ i ≤ num** 范围中的每个数字 **i** ,计算其二进制数中的 1 的数目并将它们作为数组返回。
输出: [0,1,1]
输出: [0,1,1,2,1,2]
**方法一:直接计算**
```java
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i <= num; i++){
res[i] = Integer.bitCount(i); //从0~num计算每个数字包含的1的个数
}
return res;
}
}
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 1; i <= num; i++){
res[i] = res[i&(i-1)] + 1;
}
return res;
}