【Module】【论文复现】SENet

论文: SENet.
代码: SENet.

前言：
\qquad 这篇论文就是通道维度（channel-wise）增加注意力机制，关键的两个操作是squeeze和excitation，所以论文把这个attention结构命名为SE block。
\qquad 核心思想：通过全连接网络根据loss去自动学习特征权重。
\qquad 细说：SE block是为了显式地实现特征通道的的相互依赖关系。也就是通过自动学习的方式（设计一个网络根据loss去自动学习特征权重，而不是直接根据特征通道的数值分布来判断）获取到每个特征通道的重要程度，然后用这个重要程度去给每一个特征通道赋予一个权重值，从而让神经网络重点关注某些特征通道，即提升对当前任务有用的特征通道并抑制对当前任务用处不大的特征通道。
\qquad 同时这篇论文也获得了最后一届ImageNet 2017竞赛图像分类任务的冠军，并被邀请在CVPR 2017 workshop中给出算法介绍。而且SE Block是一个轻量化的网络Block，代码简单，易于移植，所有有需要的朋友都可以放在自己的任务中试试。

一、背景

\qquad 注意力机制（Attention Mechanism）源于对人类视觉的研究。在认知科学中，由于信息处理的瓶颈，人类会选择性地关注所有信息的一部分，同时忽略其他可见的信息。实现这一能力的原因是人类视网膜的不同部位具有不一样的信息处理能力，即不同部分的敏锐度（Acuity）不同，人类视网膜中央凹部位具有最高的敏锐度。为了合理利用有限的视觉信息处理资源，人类需要选择视觉区域中的特定部分，然后重点关注它。例如人们在用电脑屏幕看电影的时候，会重点关注和处理电脑屏幕范围内的视觉，而电脑屏幕外的视觉如键盘、电脑背景等等都会被忽视。

\qquad 注意力机制最早用于自然语言处理领域（NLP），后来在计算机视觉领域（CV）也得到广泛的应用，注意力机制被引入来进行视觉信息处理。注意力机制没有严格的数学定义，例如传统的局部图像特征提取、滑动窗口方法等都可以看作一种注意力机制。在神经网络中，注意力机制通常是一个额外的神经网络，能够硬性选择输入的某些部分，或者给输入的不同部分分配不同的权重。注意力机制能够从大量信息中筛选出重要的信息。

\qquad 在神经网络中引入注意力机制有很多方法，以卷积神经网络为例，可以在空间维度增加引入attention机制（如inception网络的多尺度，让并联的卷积层有不同的权重），也可以在通道维度（channel）增加attention机制，当然也有混合维度即同时在空间维度和通道维度增加attention机制（这部分可以看我的另一篇博文链接: CBAM.)，本文举例说明attention机制的论文是获得了2017年最后一届ImageNet比赛图像分类冠军的SEnet模型（属于卷积神经网络CNN模型中的一种），该模型是在通道维度增加attention机制。

二、网络结构

通道注意力机制的具体实现过程如下图所示：

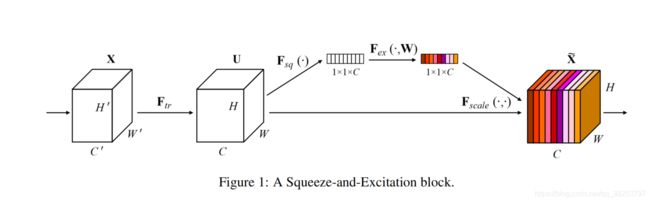
给定一个输入$X([C^{{}^{\prime }},H^{{}^{\prime }},W^{{}^{\prime }}])$，通过一系列卷积操作（$F_{tr}$）变换后得到特征$U([C,H,W])$。与传统的CNN不一样的是，接下来通过三个操作来重标定前面得到的特征。

操作1：Squeeze（$F_{sq}$）

\qquad 由于卷积只是在一个局部空间内进行操作，很难获得足够的信息来提取channel之间的关系，对于网络中前面的层这更严重，因为感受野比较小。
\qquad 为此，SENet提出Squeeze操作，将一个channel上整个空间特征编码为一个全局特征，采用global average pooling来实现将每个通道的二维特征（H×W）压缩为1个实数，论文是通过平均值池化的方式实现（原则上也可以采用更复杂的聚合策略）。这属于空间维度的一种特征压缩，因为这个实数是根据二维特征所有值算出来的，所以在某种程度上具有全局的感受野，通道数保持不变，所以通过squeeze操作后变为得到特征shape为$[C,1,1]$。

公式表示：
$$Z_c=F_{sq}(u_c)=\frac{1}{H\ast W}\sum _{i=1}^H\sum _{j=1}^W{u}_c(i,j)$$

Squeeze：一句话来说就是求每个channel对应的所有元素的均值。[C, H, W] => [C, 1, 1]，每个值都具有一个channel上的全局感受野。

操作2：excitation（$F_{ex}$）

\qquad Sequeeze操作得到了所有channel对应的全局特征，我们接下来需要另外一种运算来抓取channel之间的关系。

\qquad 为此设计了excitation操作，通过$F_{sq}$操作得来的参数（[C,1,1]）来为每个特征通道动态的生成一个权重值，这个权重值是如何生成就很关键了，论文是通过两个全连接层组成一个Bottleneck结构去建模通道间的相关性，并输出和输入特征同样数目的权重值。

\qquad 详细的$F_{sq}$操作：FC + ReLu + FC + Sigmoid。首先通过一个全连接层（FC）将特征维度降低到原来的1/r，然后经过ReLu函数激活后再通过一个全连接层（FC）生回到原来的特征维度C，然后通过sigmoid函数转化为一个0~1的归一化权重。

公式表示：
$$s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma (W_2\delta (W_{1}z))$$

注意：这里的Sequeeze操作的设计必须要满足两个要求：首先要灵活，它要可以动态的学习到各个channel之间的非线性关系；第二点是学习的关系不是互斥的，因为这里允许多channel特征，而不是one-hot形式。

Squeeze：一句话来说就是利用$F_{sq}$操作计算得到每一层的全局信息[C,1,1]，动态的生成各个channel的权重关系。

操作3：Scale（$F_{scale}$）

\qquad 最后将excitation学习到的归一化权重加权到每个通道的特征上。论文中的方法是用乘法，逐通道乘以权重系数，完成在通道维度上引入attention机制。

公式表示：
$$\widetilde{x_c}=F_{scale}(u_c,s_c)=s_c\ast u_c$$

Scale：一句话来说就是用$F_{ex}$操作计算得到的channel权重[C,1,1]，每个权重的值去乘以对应channel中的每个元素。

如果还是无法理解，也可以看下图SE-ResNetBlock结构图：

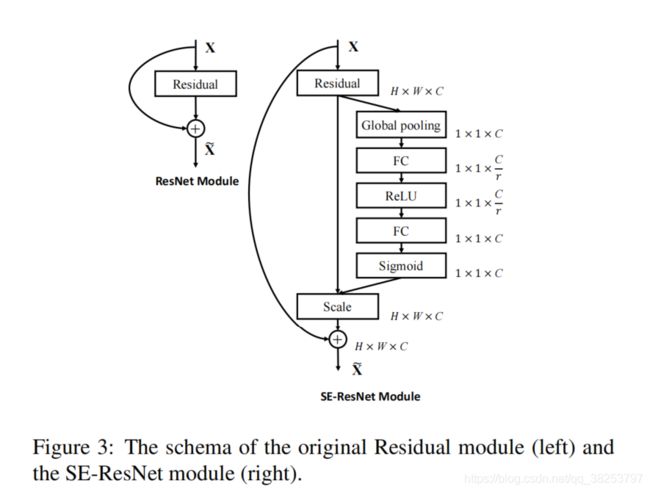
总结
\qquad 其实整个操作可以看成动态的学习到了各个channel的权重系数，从而使得模型对各个channel的特征更有辨别能力，这应该也算一种attention机制。

补充：
1、SEnet的核心思想在于通过全连接网络根据loss去自动学习特征权重（而不是直接根据特征通道的数值分布来判断），使得有效的特征通道权重大。当然，SE block不可避免地增加了一些参数和计算量，但是在效果面前，这个性价比还是很高的。
2、Sequeeze操作理论上可以选用（全局）卷积、（全局）平均池化、（全局）最大池化。作者这里选用的是平均池化，因为选用平均池化的话虽然说可能会损失掉一些极端语义信息（像素值过大/过小），但是整体而言整个feature的语义信息还是可以保存下来的；用卷积的话参数量无法控制，深度太深的话，参数量会比较大；用最大池化的话信息肯定是无法保持的，会大量的损失语义信息。
3、Excitation操作最简单就是在Global Pooling后加个C维的隐藏层，再接一个Sigmoid函数，但是这样子做的话在较深的网络时，参数量就太大了。所有论文里用了一个全连接层进行降维，再用一个全连接层进行升维，最后接一个Sigmoid激活。
3、论文认为在Excitation操作中用两个全连接层比直接用一个全连接层的好处在于：1）具有更多的非线性，可以更好地拟合通道间复杂的相关性；2）极大地减少了参数量和计算量。

三、PyTorch实现

SE-ResNet50网络结构：

SE-ResNet代码：

import torch
from torch import nn
from torchvision.models import resnet
from torchsummary import summary

# 这个模型是将SE模块加入每个ResBlock中了，还可以只加在模型开头和结尾，到底是怎么加入模型还是要看实验结果的

def conv3x3(in_channel, out_channel, stride=1, padding=1):
    """3x3 convolution with padding"""
    return nn.Conv2d(in_channel, out_channel, kernel_size=3, stride=stride, padding=padding, bias=False)

def conv1x1(in_channel, out_channel, stride=1):
    """1x1 convolution"""
    return nn.Conv2d(in_channel, out_channel, kernel_size=1, stride=stride, bias=False)

class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        # https://github.com/moskomule/senet.pytorch/blob/master/senet/se_resnet.py
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()     # x=[b,256,56,56]
        y = self.avg_pool(x).view(b, c)  # self.avg_pool(x)=>[b,256,1,1]   .view=>[b,256]
        y = self.fc(y).view(b, c, 1, 1)  # self.fc(y)=>[b,256]  .view=>[b,256,1,1]
        return x * y.expand_as(x)        # 复制[b,256,1,1] => [b,256,56,56]

class SE_BasicBlock(nn.Module):
    # resnet18 + resnet34(resdual1)  实线残差结构+虚线残差结构
    expansion = 1  # 残差结构中主分支的卷积核个数是否发生变化（倍数） 第二个卷积核输出是否发生变化

    def __init__(self, in_channel, out_channel, stride=1, downsample=None):
        """
        : params: in_channel=第一个conv的输入channel
        : params: out_channel=第一个conv的输出channel
        : params: stride=中间conv的stride
        : params: downsample=None:实线残差结构/Not None:虚线残差结构
        """
        super(SE_BasicBlock, self).__init__()
        self.conv1 = conv3x3(in_channel=in_channel, out_channel=out_channel, stride=stride)
        self.bn1 = nn.BatchNorm2d(out_channel)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(in_channel=out_channel, out_channel=out_channel)
        self.bn2 = nn.BatchNorm2d(out_channel)
        self.downsample = downsample
        self.se = SELayer(out_channel)

    def forward(self, x):
        identity = x
        if self.downsample is not None:
            identity = self.downsample(x)

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        out = self.se(out)

        out += identity
        out = self.relu(out)
        return out

class SE_Bottleneck(nn.Module):
    # resnet50+resnet101+resnet152（resdual2） 实线残差结构+虚线残差结构
    expansion = 4  # 残差结构中主分支的卷积核个数是否发生变化（倍数）  第三个卷积核输出是否发生变化

    def __init__(self, in_channel, out_channel, stride=1, downsample=None):
        """
        : params: in_channel=第一个conv的输入channel
        : params: out_channel=第一个conv的输出channel
        : params: stride=中间conv的stride
                  resnet50/101/152:conv2_x的所有层s=1   conv3_x/conv4_x/conv5_x的第一层s=2,其他层s=1
        : params: downsample=None:实线残差结构/Not None:虚线残差结构
        """
        super(SE_Bottleneck, self).__init__()
        # 1x1卷积一般s=1 p=0 => w、h不变   卷积默认向下取整
        self.conv1 = conv1x1(in_channel=in_channel, out_channel=out_channel, stride=1)
        self.bn1 = nn.BatchNorm2d(out_channel)
        # ----------------------------------------------------------------------------------
        # 3x3卷积一般s=2 p=1 => w、h /2（下采样）     3x3卷积一般s=1 p=1 => w、h不变
        self.conv2 = conv3x3(in_channel=out_channel, out_channel=out_channel, stride=stride)
        self.bn2 = nn.BatchNorm2d(out_channel)
        # ---------------------------------------------------------------------------------
        self.conv3 = conv1x1(in_channel=out_channel, out_channel=out_channel * self.expansion, stride=1)
        self.bn3 = nn.BatchNorm2d(out_channel * self.expansion)
        # ----------------------------------------------------------------------------------
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample

        self.se = SELayer(out_channel * self.expansion)

    def forward(self, x):
        identity = x
        if self.downsample is not None:
            identity = self.downsample(x)

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        out = self.se(out)

        out += identity
        out = self.relu(out)
        return out

class SE_ResNet(nn.Module):

    def __init__(self, block, blocks_num, num_classes=1000):
        """
        : params:  block=BasicBlock/Bottleneck
        : params:  blocks_num=每个layer中残差结构的个数
        : params:  num_classes=数据集的分类个数
        """
        super(SE_ResNet, self).__init__()
        self.in_channel = 64  # in_channel=每一个layer层第一个卷积层的输出channel/第一个卷积核的数量

        self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(self.in_channel)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)  # 池化默认向下取整

        # 第1个layer的虚线残差结构只需要改变channel,长、宽不变  所以stride=1
        self.layer1 = self._make_layer(block, blocks_num[0], channel=64, stride=1)
        # 第2/3/4个layer的虚线残差结构不仅要改变channel还要将长、宽缩小为原来的一半 所以stride=2
        self.layer2 = self._make_layer(block, blocks_num[1], channel=128, stride=2)
        self.layer3 = self._make_layer(block, blocks_num[2], channel=256, stride=2)
        self.layer4 = self._make_layer(block, blocks_num[3], channel=512, stride=2)

        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))  # AdaptiveAvgPool2d 自适应池化层  output_size=(1, 1)
        self.fc = nn.Linear(512 * block.expansion, num_classes)

        # 凯明初始化
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
            elif isinstance(m, (nn.BatchNorm2d, nn.GroupNorm)):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)

    def _make_layer(self, block, block_num, channel, stride=1):
        """
        : params: block=BasicBlock/Bottleneck   18/34用BasicBlock   50/101/152用Bottleneck
        : params: block_num=当前layer中残差结构的个数
        : params: channel=每个convx_x中第一个卷积核的数量  每一个layer的这个参数都是固定的
        : params: stride=每个convx_x中第一层中3x3卷积层的stride=每个convx_x中downsample(res)的stride
                  resnet50/101/152   conv2_x=>s=1  conv3_x/conv4_x/conv5_x=>s=2
        """
        downsample = None

        # in_channel:每个convx_x中第一层的第一个卷积核的数量
        # channel*block.expansion:每一个layer最后一个卷积核的数量
        # res50/101/152的conv2/3/4/5_x的in_channel != channel * block.expansion永远成立，所以第一层必有downsample（虚线残差结构）
        # 但是conv2_x的第一层只改变channel不改变w/h（s=1），而conv3_x/conv4_x/conv5_x的第一层不仅改变channel还改变w/h(s=2下采样)
        if stride != 1 or self.in_channel != channel * block.expansion:
            downsample = nn.Sequential(
                nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(channel * block.expansion)
            )

        layers = []
        # 第一层（含虚线残差结构）加入layers
        layers.append(block(self.in_channel, channel, stride=stride, downsample=downsample))
        # 经过第一层后channel变了
        self.in_channel = channel * block.expansion

        # res50/101/152的conv2/3/4/5_x除了第一层有downsample（虚线残差结构），其他所有层都是实现残差结构（等差映射）
        for _ in range(1, block_num):
            layers.append(block(self.in_channel, channel))  # channel在Bottleneck变化：512->128->512
        return nn.Sequential(*layers)

    def forward(self, x):
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.maxpool(out)

        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)

        out = self.avgpool(out)
        out = torch.flatten(out, 1)
        out = self.fc(out)
        return out

def se_resnet18(num_classes=5):
    return SE_ResNet(SE_BasicBlock, [2, 2, 2, 2], num_classes=num_classes)

def se_resnet34(num_classes=5):
    # 预训练权重 https://download.pytorch.org/models/resnet34-333f7ec4.pth
    return SE_ResNet(SE_BasicBlock, [3, 4, 6, 3], num_classes=num_classes)

def se_resnet50(num_classes=5):
    # 预训练权重 https://download.pytorch.org/models/resnet50-19c8e357.pth
    return SE_ResNet(SE_Bottleneck, [3, 4, 6, 3], num_classes=num_classes)

def se_resnet101(num_classes=5):
    # 预训练权重 https://download.pytorch.org/models/resnet101-5d3b4d8f.pth
    return SE_ResNet(SE_Bottleneck, [3, 4, 23, 3], num_classes=num_classes)

def se_resnet152(num_classes=5):
    return SE_ResNet(SE_Bottleneck, [3, 8, 36, 3], num_classes=num_classes)


if __name__ == '__main__':
    # 权重测试
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    print(device)

    model = se_resnet50().to(device)
    print(model)
    summary(model, (3, 224, 224))  # params:26,033,221    Total Size (MB): 428.90

四、实验结果

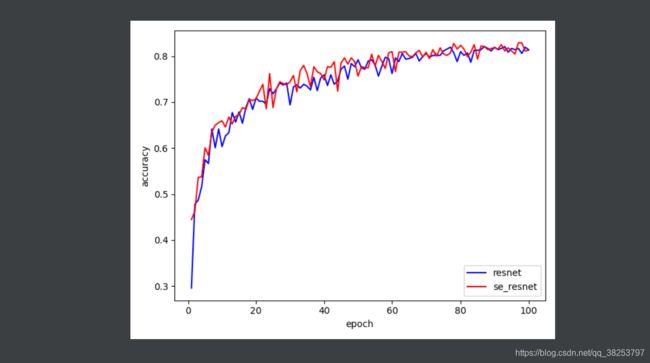
提升的很小，不知道是不是我的数据集的问题，建议大家使用的时候多实验，自己判断需不需要用。

Reference

https://blog.csdn.net/Amigo_1997/article/details/105948497
https://zhuanlan.zhihu.com/p/65459972/
https://www.bilibili.com/video/BV1Up4y187qb?from=search&seid=808281711223926860