《剑指offer》python版本 分类刷题(下)
文章目录
- 7/30
- 7/31 and 8/1
- 8/2
- 8/3
- 8/4
- 8/5
- 8.6
- 8.7
- 8/10
- 8/11
7/30
- 用两个栈实现队列
题目描述
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
解题思路
队列的Push就是直接进栈;Pop:节点进入stack1,然后再stack1的元素pop出,push到stack2中,stack2再pop出来就是先进先出的顺序了。
步骤:
- 判断stack2是否为空,不为空就pop
- 将stack1的节点pop出,然后push进stack2,再将stack2的元素pop。
class Solution:
def __init__(self):
self.stack1 = []
self.stack2 = []
def push(self, node):
# write code here
self.stack1.append(node)
def pop(self):
if self.stack2:
return self.stack2.pop()
while self.stack1:
self.stack2.append(self.stack1.pop())
return self.stack2.pop()
题目描述
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
- 包含min函数的栈
题目描述
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
解题思路
借助最小元素辅助栈。每次压栈操作时, 如果压栈元素比当前最小元素更小, 就把这个元素压入最小元素栈, 原本的最小元素就成了次小元素. 同理, 弹栈时, 如果弹出的元素和最小元素栈的栈顶元素相等, 就把最小元素的栈顶弹出.
class Solution:
def __init__(self):
self.stack1 = []
self.assist = []
def push(self, node):
# 压栈的时候,如果主栈的压入大于辅助栈压入,辅助栈不压;小于等于,则同时压入
if not self.assist: #辅助栈如果为空,则压入
self.assist.append(node)
else: # 比较要压入元素和辅助栈当前栈顶元素(也就是最小元素),判断是否压入
self.assist.append(min(self.assist[-1],node))
self.stack1.append(node)
def pop(self):
# 出栈的时候,辅助栈也要跟着一块出,这么做是要保证辅助栈栈顶元素始终是主栈元素中最小的
if self.stack1:
self.assist.pop()
return self.stack1.pop()
def top(self):
if self.stack1:
return self.stack1[-1]
def min(self):
if self.assist:
return self.assist[-1]
- 栈的压入、弹出序列
题目描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
解题思路:看的别人的,觉得很好理解
假设有一串数字要将他们压栈: 1 2 3 4 5
如果这个栈是很大很大,那么一次性全部压进去,再出栈:5 4 3 2 1
但是,如果这个栈高度为4,会发生什么? 1 2 3 4都顺利入栈,但是满了,那么要先出栈一个,才能入栈,那么就是先出4,然后压入5,随后再全部出栈:4 5 3 2 1
那么我总结了所有可能的出栈情况:
5 4 3 2 1//栈高度为5
4 5 3 2 1//栈高度为4
3 4 5 2 1//栈高度为3
2 3 4 5 1//栈高度为2
1 2 3 4 5//栈高度为1
借助一个辅助的栈,遍历压栈的顺序,依次放进辅助栈中。
对于每一个放进栈中的元素,栈顶元素都与出栈的popIndex对应位置的元素进行比较,是否相等,相等则popIndex++,再判断,直到为空或者不相等为止。
class Solution:
def IsPopOrder(self, pushV, popV):
# write code here
stack = []
for i in pushV:
stack.append(i)
while stack[-1] == popV[0]:
stack.pop()
popV.pop(0)
if not popV:
return True
return False
7/31 and 8/1
- 滑动窗口的最大值
题目描述
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
解题思路:
用一个队列实现,初始化时,size个数字进入队列,找出队列中的最大值;随后一个数字出队,一个数字进队,直到全部进队。虽然也通过了,但我觉得自己代码写的很烂。
class Solution:
def maxInWindows(self, num, size):
# write code here
"""
用一个队列实现,初始化时,size个数字进入队列,找出队列中的最大值;随后一个数字出队,一个数字进队,直到全部进队
"""
if size == 0 or size > len(num):
return []
queue = []
res = []
for i in range (size):
queue.append(num[i])
res.append(max(queue))
for i in range(size, len(num)):
queue.pop(0)
queue.append(num[i])
res.append(max(queue))
return res
- 矩阵中的路径
题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
解题思路:
典型的回溯法题目。我觉得第一次做这种题直接去看书上解析了,自己不可能想出来 ==
打算整理一篇回溯法的博客。
首先,遍历这个矩阵,我们很容易就能找到与字符串str中第一个字符相同的矩阵元素ch。然后遍历ch的上下左右四个字符,如果有和字符串str中下一个字符相同的,就把那个字符当作下一个字符(下一次遍历的起点),如果没有,就需要回退到上一个字符,然后重新遍历。为了避免路径重叠,需要一个辅助矩阵来记录路径情况。
下面代码中,当矩阵坐标为(i,j)的格子和路径字符串中下标为pathLength的字符一样时,从4个相邻的格子(i,j-1)、(i-1,j)、(i,j+1)以及(i+1,j)中去定位路径字符串中下标为pathLength+1的字符。
如果4个相邻的格子都没有匹配字符串中下标为pathLength+1的字符,表明当前路径字符串中下标为pathLength的字符在矩阵中的定位不正确,我们需要回到前一个字符串(pathLength-1),然后重新定位。
一直重复这个过程,直到路径字符串上所有字符都在矩阵中找到格式的位置(此时str[pathLength] == ‘\0’)
class Solution:
def hasPath(self, matrix, rows, cols, path):
# write code here
if not matrix and rows <= 0 and cols <= 0 and path == None:
return False
boolmatrix = [0] * (rows * cols)
pathLength = 0
for i in range(rows):
for j in range(cols):
if self.hasPathCore(matrix, rows, cols, i, j, path, pathLength, boolmatrix):
return True
return False
def hasPathCore(self, matrix, rows, cols, i, j, path, pathLength, boolmatrix):
if len(path) == pathLength:
return True
hasNextPath = False
if (i >= 0 and i < rows and j >= 0 and j < cols and
matrix[i * cols + j] == path[pathLength] and not boolmatrix[i * cols + j]):
pathLength += 1
boolmatrix[i * cols + j] = True
# 进行该值的上下左右的递归(周围是否存在下一个路径点)
hasNextPath = (self.hasPathCore(matrix, rows, cols, i - 1, j, path, pathLength, boolmatrix)
or self.hasPathCore(matrix, rows, cols, i, j + 1, path, pathLength, boolmatrix)
or self.hasPathCore(matrix, rows, cols, i + 1, j, path, pathLength, boolmatrix)
or self.hasPathCore(matrix, rows, cols, i, j - 1, path, pathLength, boolmatrix))
# 对标记矩阵进行布尔值标记
if not hasNextPath: # 说明周围4个点都不存在下一路径
pathLength -= 1 # 回到前一个字符
boolmatrix[i * cols + j] = False # 将该点重新设为未标记
return hasNextPath
- 机器人的运动范围
题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
解题思路:
本题与矩阵中的路径思想一致,都是使用回溯法解决问题,只不过对于位置的约束条件的不同。
将地图全部置1,遍历能够到达的点,将遍历的点置0并令计数+1.这个思路在找前后左右相连的点很有用。
class Solution:
def movingCount(self, threshold, rows, cols):
# write code her
Matrix = [[1 for i in range(cols)] for j in range(rows)]
count = self.findway(threshold, 0, 0, Matrix)
print(Matrix)
return count
def findway(self, threshold, i, j, Matrix):
count = 0
if i >= 0 and j>= 0 and i < len(Matrix) and j < len(Matrix[0]) and Matrix[i][j] \
and sum(map(int, str(i) + str(j))) <= threshold:
Matrix[i][j] = 0
count = 1+self.findway(threshold, i+1, j, Matrix)\
+ self.findway(threshold, i-1, j, Matrix)\
+ self.findway(threshold, i, j+1, Matrix)\
+ self.findway(threshold, i, j-1, Matrix)
return count
8/2
- 求1+2+3+…+n
题目描述
求1+2+3+…+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
class Solution:
def Sum_Solution(self, n):
# write code here
sum = n
temp = sum and self.Sum_Solution(n-1)
sum = sum + temp
return sum
- 二进制中1的个数
如果一个整数不为0,那么这个整数至少有一位是1。如果我们把这个整数减1,那么原来处在整数最右边的1就会变为0,原来在1后面的所有的0都会变成1(如果最右边的1后面还有0的话)。其余所有位将不会受到影响。
举个例子:一个二进制数1100,从右边数起第三位是处于最右边的一个1。减去1后,第三位变成0,它后面的两位0变成了1,而前面的1保持不变,因此得到的结果是1011.我们发现减1的结果是把最右边的一个1开始的所有位都取反了。这个时候如果我们再把原来的整数和减去1之后的结果做与运算,从原来整数最右边一个1那一位开始所有位都会变成0。如1100&1011=1000.也就是说,把一个整数减去1,再和原整数做与运算,会把该整数最右边一个1变成0.那么一个整数的二进制有多少个1,就可以进行多少次这样的操作。
class Solution:
def NumberOf1(self, n):
# write code here
count = 0
while n:
n = (n - 1) & n
count = count + 1
return count
别的解法:
class Solution:
def NumberOf1(self, n):
# write code here
if n>=0:
return bin(n).count('1')
else:
return bin(2**32+n).count('1')
- 数值的整数次方
题目描述
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
保证base和exponent不同时为0
这一题的意义是?
class Solution:
def Power(self, base, exponent):
# write code here
return base**exponent
别的解法:使用快速幂
传统的幂运算,是对底数进行连乘,时间复杂度为o(n),例如:2^13 = 222……*2,连乘十三次。
利用指数的二进制,可以实现复杂度为o(logn)的幂运算。还是以2^13为例,13的二进制为1101,因此2的13次方可以分解成以下形式:

和13的二进制1101相对比,只要二进制为1的位,就有权重,权重为2^(i-1),i表示第几位,1101从右到左,依次为第1位,第2位,第3位,第4位。
下面的工作就是如何确定二进制中的哪一位为1,这里可以利用位运算中的&和>>运算。由于1的二进制除了第一位是1,其他的全是0,因此可以利用n&1是否为0来判断n的二进制的当前最低位是否为1,如果n&1等于0,说明当前n的最低位不为1。利用右移运算来逐位读取。
# -*- coding:utf-8 -*-
class Solution:
def Power(self, base, exponent):
# write code here
e = abs(exponent)
res = 1
while e:
if e & 1: # 判断当前的最后一位是否为1,如果为1的话,就需要把之前的幂乘到结果中。
res *= base
base *= base # 一直累乘,如果最后一位不是1的话,就不用了把这个值乘到结果中,但是还是要乘。
e = e >> 1
return res if exponent>=0 else 1/res
8/3
- 顺时针打印矩阵
思路: 先取矩阵的第一行,接着将剩下作为新矩阵进行一个逆时针90度的翻转,接着获取第一行,直到矩阵为空。
class Solution:
# matrix类型为二维列表,需要返回列表
def printMatrix(self, matrix):
# write code here
res = []
while matrix:
res += matrix.pop(0)
if matrix:
matrix = self.rotate(matrix)
return res
def rotate(self, matrix):
# 逆时针旋转矩阵
rows = len(matrix)
cols = len(matrix[0])
new_matrix = []
# 行列调换
for i in range(cols):
new_line = []
for j in range(rows):
new_line.append(matrix[j][cols-1-i])
new_matrix.append(new_line)
return new_matrix
- 最小的K个数
题目描述
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。
这题考排序,需要整理一下几个排序问题。
class Solution:
def GetLeastNumbers_Solution(self, tinput, k):
# write code herene
if not tinput or k<=0 or k>len(tinput):
return []
tinput.sort()
return tinput[:k]
- 整数中1出现的次数(从1到n整数中1出现的次数)
题目描述:
求出113的整数中1出现的次数,并算出1001300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数(从1 到 n 中1出现的次数)。
解题思路:
胡乱写的,顺利的不可思议(发呆)
我不能再这样了 ==
class Solution:
def NumberOf1Between1AndN_Solution(self, n):
# write code here
s = ''
for i in range(n+1):
s += str(i)
return s.count('1')
8/4
- 扑克牌顺子
# -*- coding:utf-8 -*-
class Solution:
def IsContinuous(self, numbers):
# write code here
if not numbers:
return False
numbers.sort()
zeros = numbers.count(0)
for i in range(zeros,4):
if numbers[i+1] == numbers[i]:return False
zeros -= numbers[i+1]-numbers[i]-1
if zeros < 0:
return False
return True
- 和为S的两个数字
题目描述:
输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
解题思路:
数列满足递增,设两个头尾两个指针i和j,
若ai + aj == sum,就是答案(相差越远乘积越小,例如和为10,1×9是乘积最小的。)
若ai + aj > sum,aj肯定不是答案之一(前面已得出 i 前面的数已是不可能),j -= 1
若ai + aj < sum,ai肯定不是答案之一(前面已得出 j 后面的数已是不可能),i += 1
class Solution:
def FindNumbersWithSum(self, array, tsum):
# write code here
i = 0
j = len(array)-1
while i < j:
if array[i] + array[j] < tsum:
i += 1
elif array[i] + array[j] > tsum:
j -= 1
elif array[i]+array[j] == tsum:
return array[i], array[j]
return []
- 和为S的连续正数序列
题目描述
小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!
解题思路:
跟上一题挺像的,用滑动窗口来实现
# -*- coding:utf-8 -*-
class Solution:
def FindContinuousSequence(self, tsum):
# write code here
if tsum < 3:
return []
# 初始化滑动窗口
small = 1
big = 2
res = []
while small < big:
curSum = sum(range(small,big+1))
if curSum == tsum:
# 找到一组解,添加到res
res.append(range(small, big+1))
# 移动滑动窗口继续寻找
big += 1
elif curSum < tsum:
big += 1
elif curSum > tsum:
small += 1
return res
8/5
- 丑数
题目描述
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
解题思路
因为丑数只包含质因子2,3,5,假设我们已经有n-1个丑数,按照顺序排列,且第n-1的丑数为M。那么第n个丑数一定是由这n-1个丑数分别乘以2,3,5,得到的所有大于M的结果中,最小的那个数。
事实上我们不需要每次都计算前面所有丑数乘以2,3,5的结果,然后再比较大小。因为在已存在的丑数中,一定存在某个数T2,在它之前的所有数乘以2都小于已有丑数,而T2×2的结果一定大于M,同理,也存在这样的数T3,T5,我们只需要标记这三个数即可。
# -*- coding:utf-8 -*-
class Solution:
def GetUglyNumber_Solution(self, index):
# write code here
if index == 0:
return 0
# 1作为特殊数直接保存
baselist = [1]
min2 = min3 = min5 = 0
curnum = 1
while curnum < index:
minnum = min(baselist[min2] * 2, baselist[min3] * 3, baselist[min5] * 5)
baselist.append(minnum)
# 找到第一个乘以2的结果大于当前最大丑数M的数字,也就是T2
while baselist[min2] * 2 <= minnum:
min2 += 1
# 找到第一个乘以3的结果大于当前最大丑数M的数字,也就是T3
while baselist[min3] * 3 <= minnum:
min3 += 1
# 找到第一个乘以5的结果大于当前最大丑数M的数字,也就是T5
while baselist[min5] * 5 <= minnum:
min5 += 1
curnum += 1
return baselist[-1]
- 孩子们的游戏(圆圈中最后剩下的数)
题目描述
每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0…m-1报数…这样下去…直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!_)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1)
如果没有小朋友,请返回-1
约瑟夫环问题:
方法1:使用list模拟循环链表,用cur作为指向list的下标位置。
当cur移到list末尾直接指向list头部,当删除一个数后list的长度和cur的值相等则cur指向0
# -*- coding:utf-8 -*-
class Solution:
def LastRemaining_Solution(self, n, m):
# write code here
if n < 1 or m < 1:
return -1
n_list = [i for i in range(n)] # 列表模拟
# print(nlist)
cur = 0 # 指向nlist的指针
while len(n_list) >1:
for i in range(1, m):
cur += 1
# 当指针移到nlist的末尾,就把指针指向nlist的头
if cur == len(n_list):
cur = 0
# 删除一个数,此时由于删除后nlist的下标随之变化,因此cur指向的便是原数组中的下一个数字,此时cur不需要移动
n_list.remove(n_list[cur])
if cur == len(n_list):
cur = 0
return n_list[0]
方法2:找规律
使用动态规划。注意到,输入的序列在删除一个元素后,序列的长度会改变,如果索引
在被删除的元素位置开始计算,那么每删除一个元素,序列的长度减一而索引会完全改变。
如果能找到改变前的索引和新索引的对应关系,那么该问题就容易解决了。
我们定义一个函数f(n, m),表示每次在n个数字0,1,2,3,…,n-1中每次删除第m个数字后剩下
的数字。那么第一个被删除的数字的索引是(m-1)%n。删除该索引元素后,剩下的n-1个数字
为0,1,2,…,k-1,k+1,…,n-1。下次删除数字是重k+1位置开始,于是可以把序列看
作k+1,…,n-1,0,1,…,k-1。该序列最后剩下的序列也是f的函数。但该函数和第一个函数
不同,存在映射关系,使用f’来表示,于是有:f(n, m)=f’(n-1, m)。接下来需要找到映射关系。
k+1 --> 0
k+2 --> 1
.
.
.
n-1 --> n-k-2
0 --> n-k-1
.
.
.
k-1 --> n-2
所以可以得到:right = left-k-1,则p(x) = (x-k-1)%n,而逆映射是p’(x) = (x+k+1)%n
即0n-1序列中最后剩下的数字等于(0n-2序列中最后剩下的数字+k)%n,很明显当n=1时,
只有一个数,那么剩下的数字就是0.问题转化为动态规划问题,关系表示为:
f(n)=(f(n-1)+m)%n; 当n=1,f(1)=0;
class Solution:
def LastRemaining_Solution(self, n, m):
# write code here
if n < 1 or m < 1:
return -1
last = 0
for i in range(2, n+1):
last = (last+m)%i
return last
- 不用加减乘除做加法
题目描述
写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
解题思路:
【参考牛客上票数最高的解答】
首先看十进制是如何做的: 5+7=12,三步走
-
第一步:相加各位的值,不算进位,得到2。
-
第二步:计算进位值,得到10. 如果这一步的进位值为0,那么第一步得到的值就是最终结果。
-
第三步:重复上述两步,只是相加的值变成上述两步的得到的结果2和10,得到12。
同样我们可以用三步走的方式计算二进制值相加: 5-101,7-111
-
第一步:相加各位的值,不算进位,得到010,二进制每位相加就相当于各位做异或操作,101^111。
-
第二步:计算进位值,得到1010,相当于各位做与操作得到101,再向左移一位得到1010,(101&111)<<1。
-
第三步重复上述两步, 各位相加 010^1010=1000,进位值为100=(010&1010)<<1。
继续重复上述两步:1000^100 = 1100,进位值为0,跳出循环,1100为最终结果。
# -*- coding:utf-8 -*-
class Solution:
def Add(self, num1, num2):
# write code here
while(num2):
num1,num2 = (num1^num2) & 0xFFFFFFFF,((num1&num2)<<1) & 0xFFFFFFFF
return num1 if num1<=0x7FFFFFFF else ~(num1^0xFFFFFFFF)
(1) 越界检查
就是答案中的 & 0xFFFFFFFF 操作,其中 & 是按位与, 0xFFFFFFFF代表16进制下的边界 (按二进制表示的话,对应4*8=32位)。
由于python长整数类型可以表示无限位,所以需要人为设置边界,避免死循环。
设置成32位应该是考虑到其他语言的特点,测试样例中不会出现超过32位整型的数,实际上,把边界调大的话,不会影响最终结果。
(2)正负数判断及还原
正数与边界数 按位与(&) 操作后 仍得到这个数本身,负数与边界数 按位与(&) 操作后 得到的是对应二进制数的真值。答案中,通过查看符号位(最高位,即与0x7FFFFFF比较大小)判断a为正数还是负数,正数则直接返回。负数则返回~(a^0xFFFFFFFF)。 (注: ~ 表示按位取反)
8.6
- 字符流中第一个不重复的字符
class Solution:
# 返回对应char
def __init__(self):
self.s = ''
self.charDic = {
}
def FirstAppearingOnce(self):
# write code here
for key in self.s:
if self.charDic[key] == 1:
return key
return '#'
def Insert(self, char):
# write code here
self.charDic[char] = 1 if char not in self.charDic else self.charDic[char]+1
self.s += char
- 数据流中的中位数
# -*- coding:utf-8 -*-
class Solution:
def __init__(self):
self.s = []
def Insert(self, num):
# write code here
self.s.append(num)
def GetMedian(self, n=None):
# write code here
self.s.sort()
l = len(self.s)
if l%2:
return self.s[(l-1)//2]
else:
return (self.s[l//2] + self.s[l//2-1])/2.
不过这么写没有什么意义,看了别人写的:
使用两个堆:
大根堆:large保存大的半数的数据
小根堆:small保存小的半数的数据
获取中位数的时间复杂度为O(1),插入一个数据的时间复杂度为O(log(n))
核心思路:
1.维护一个大顶堆,一个小顶堆,且保证两点:
-
1)小顶堆里的全大于 大顶堆里的;
-
2)2个堆个数的差值小于等于1
2.当insert的数字个数为奇数时:使小顶堆个数比大顶堆多1;当insert的数字个数为偶数时,使大顶堆个数跟小顶堆个数一样。
3.那么当总数字个数为奇数时,中位数就是小顶堆堆头;当总数字个数为偶数时,中位数就是 2个堆堆头平均数
# -*- coding:utf-8 -*-
from heapq import *
class Solution:
def __init__(self):
self.heaps = [], []
def Insert(self, num):
# write code here
small, large = self.heaps
heappush(small, -heappushpop(large, num))#将num放入大根堆,并弹出大根堆的最小值,取反,放入大根堆small
if len(large) < len(small):
heappush(large, -heappop(small)) #弹出small中最小的值,取反,即最大的值,放入large
def GetMedian(self,ss):
# write code here
small,large = self.heaps
if len(large) > len(small):
return float(large[0])
return (large[0] - small[0]) /2.0
- 滑动窗口的最大值
# -*- coding:utf-8 -*-
class Solution:
def maxInWindows(self, num, size):
# write code here
if size > len(num) or size==0:
return []
res = []
q = []
for i in range(size):
q.append(num[i])
res.append(max(q))
for i in range(size, len(num)):
q.pop(0)
q.append(num[i])
res.append(max(q))
return res
- 连续子数组的最大和
思路分析
1、状态方程 : max( dp[ i ] ) = getMax( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )
2、上面式子的意义是:我们从头开始遍历数组,遍历到数组元素 arr[ i ] 时,连续的最大的和 可能为 max( dp[ i -1 ] ) + arr[ i ] ,也可能为 arr[ i ] ,做比较即可得出哪个更大,取最大值。时间复杂度为 n。
# -*- coding:utf-8 -*-
class Solution:
def FindGreatestSumOfSubArray(self, array):
# write code here
res = array[0] #记录当前所有子数组的和的最大值
maxSum = array[0] #包含array[i]的连续数组最大值
for i in array[1:]:
maxSum = max(maxSum+i, i)
res = max(maxSum, res)
return res
- 数组中出现次数超过一半的数字
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
length = len(numbers)
if length < 1:
return 0
for i in numbers:
if numbers.count(i) > length//2:
return i
return 0
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
length = len(numbers)
if length < 1:
return 0
numDict = {
}
for i in numbers:
numDict[i] = 1 if i not in numDict else numDict[i]+1
if numDict[i] > length // 2:
return i
return 0
没啥意义,看看别人写的。
思路一: 数组排序后,如果符合条件的数存在,则一定是数组中间那个数。(比如:1,2,2,2,3;或2,2,2,3,4;或2,3,4,4,4等等)这种方法虽然容易理解,但由于涉及到快排sort,其时间复杂度为O(NlogN)并非最优;
思路二: 如果有符合条件的数字,则它出现的次数比其他所有数字出现的次数和还要多。
在遍历数组时保存两个值:一是数组中一个数字,一是次数。遍历下一个数字时,若它与之前保存的数字相同,则次数加1,否则次数减1;若次数为0,则保存下一个数字,并将次数置为1。遍历结束后,所保存的数字即为所求。然后再判断它是否符合条件即可。
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
# 遍历每个元素并记录次数;若与前一个元素相同,次数加1,否者次数减1
checkNum = numbers[0]
cnt = 1
for n in numbers[1:]:
if cnt == 0: # 如果计数器为0,换下一个元素,并把计数器置为1
checkNum = n
cnt = 1
elif n == checkNum:
cnt+=1 # 相同加一
else:
cnt-=1 # 不同减一
# 检查找的的这个数是否符合条件,即出现次数是否大于数组长度的一半
if cnt>0:
cnt1 = 0
for n in numbers:
if n == checkNum:
cnt1+=1
return checkNum if cnt1 > len(numbers)//2 else 0
return 0
8.7
- 调整数组顺序使奇数位于偶数前面
class Solution:
def reOrderArray(self, array):
# write code here
res = []
if not array:
return []
for i in array:
if i%2==1:
res.append(i)
for i in array:
if i%2==0:
res.append(i)
return res
- 把数组排成最小的数
# -*- coding:utf-8 -*-
class Solution:
def PrintMinNumber(self, numbers):
# write code here
res = sorted(numbers,cmp=self.compare)
return ''.join(str(x) for x in res)
def compare(self,num1,num2):
num1 = str(num1)
num2 = str(num2)
if int(num1+num2) > int(num2+num1):
return 1
elif int(num1+num2) < int(num2+num1):
return -1
else:
return 0
- 数组中的逆序对
# -*- coding:utf-8 -*-
from collections import deque
class Solution:
def __init__(self):
self.count = 0
def InversePairs(self, data):
# write code here
self.mergeSort(data)
return self.count%1000000007
def mergeSort(self,lis):
if len(lis) <= 1:
return lis
middle = int(len(lis)//2)
left = self.mergeSort(lis[:middle])
right = self.mergeSort(lis[middle:])
return self.merge(left, right)
def merge(self,left,right):
merged,left,right = deque(), deque(left), deque(right)
while left and right:
if left[0] > right[0]:
self.count+= len(left)
merged.append(right.popleft())
else:
merged.append(left.popleft())
if right:
merged.extend(right)
else:
merged.extend(left)
return merged
8/10
- 数据在数组中出现的次数
题目描述
统计一个数字在升序数组中出现的次数。
解题思路:
二分查找,分别查找出连续数字的开始位置和结束位置
# -*- coding:utf-8 -*-
class Solution:
def GetNumberOfK(self, data, k):
# write code here
return self.getEnd(data,k) - self.getStart(data, k) + 1
def getStart(self,data,k):
start = 0
end = len(data) - 1
mid = (start+end)//2
while start<=end:
if data[mid]<k:
start = mid +1
else:
end = mid - 1
mid = (start+end)//2
return start
def getEnd(self,data,k):
start = 0
end = len(data) - 1
mid = (start+end)//2
while start<=end:
if data[mid]<=k:
start = mid +1
else:
end = mid - 1
mid = (start + end)//2
return end
- 数组中只出现一次的数字
题目描述
一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
# -*- coding:utf-8 -*-
class Solution:
# 返回[a,b] 其中ab是出现一次的两个数字
def FindNumsAppearOnce(self, array):
# write code here
# 异或操作
res = 0
for i in array:
res = res ^ i
# 获取res中最低位为1的位置
idx = 0
while(res&1) == 0:
res >>=1
idx+=1
a = b = 0
for i in array:
if self.isBit(i, idx):
a = a ^ i
else:
b = b ^ i
return a, b
# 判断num的二进制从低到高idx位是不是1
def isBit(self, num, idx):
num = num >> idx
return num & 1
- 数组中重复的数字
题目描述
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
解题:挺简单的,使用哈希字典
# -*- coding:utf-8 -*-
class Solution:
# 这里要特别注意~找到任意重复的一个值并赋值到duplication[0]
# 函数返回True/False
def duplicate(self, numbers, duplication):
# write code here
dic = {
}
for num in numbers:
if not num in dic:
dic[num] = 1
else:
dic[num] += 1
for num in numbers:
if dic[num] > 1:
duplication[0] = num
return True
return False
8/11
- 复杂链表的复杂(填坑)
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
解题:分三步走
第一步:先把原来的链表复制一份,复制的节点就放在原节点的后面
第二步:复制random指针,让新的节点的random指针指向旧节点random指针的后面
第三步:分离两个链表就可以了
# -*- coding:utf-8 -*-
# class RandomListNode:
# def __init__(self, x):
# self.label = x
# self.next = None
# self.random = None
class Solution:
# 返回 RandomListNode
def Clone(self, pHead):
# write code here
if pHead == None:
return
# 第一步,完成链表节点的复制和单项指针的重指向
kk = pHead
while kk:
node = RandomListNode(kk.label) # 复制一个节点出来
# 这两句让新节点和链表做了左右相连
node.next = kk.next
kk.next = node
# 对链表的下一个节点做同样的操作
kk = node.next
# 第二步,复制random节点
kk = pHead
while kk:
if kk.random:
kk.next.random = kk.random.next
kk = kk.next.next
# 第三步,分离两个链表
kk = pHead
ee = pHead.next
nn = pHead.next
while kk:
# 让旧的next指针指向下一个旧节点
kk.next = kk.next.next
if nn.next:
# 让新的节点的next指针指向下一个新节点
nn.next = nn.next.next
nn = nn.next
kk = kk.next
return ee
- 构建乘积数组
题目描述
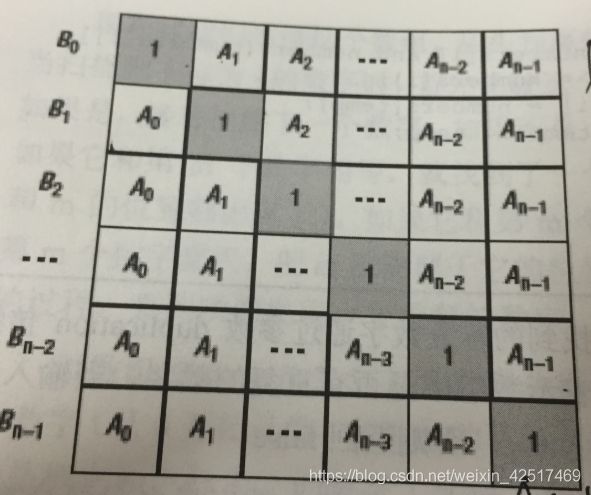
给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…*A[i-1]A[i+1]…*A[n-1]。不能使用除法。(注意:规定B[0] = A[1] * A[2] * … * A[n-1],B[n-1] = A[0] * A[1] * … * A[n-2];)
对于A长度为1的情况,B无意义,故而无法构建,因此该情况不会存在。
剑指的思路:
B[i]的值可以看作下图的矩阵中每行的乘积。
下三角用连乘可以很容求得,上三角,从下向上也是连乘。
因此我们的思路就很清晰了,先算下三角中的连乘,即我们先算出B[i]中的一部分,然后倒过来按上三角中的分布规律,把另一部分也乘进去。
解题:
class Solution:
def multiply(self, A):
if not A:
return []
length = len(A)
B = [None]*length
B[0]=1
for i in range(1,length):
B[i] = B[i-1]*A[i-1]
tmp = 1
for j in range(length-2,-1,-1):
tmp *= A[j+1]
B[j] *= tmp
return B
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
stack = []
while pHead:
stack.append(pHead)
pHead = pHead.next
if pHead in stack:
return pHead
return
- 剪绳子
题目描述
给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1,m<=n),每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
class Solution:
def cutRope(self, number):
# write code here
#动态规划,自下向上解决问题
if number < 2:
return 0
if number == 2:
return 1
if number == 3:
return 2
#保存结果的数组,
result = [0,1,2,3]
for i in range(4, number+1):
max = 0
for j in range(1,i/2+1):
temp = result[j]*result[i-j]
if temp > max:
max = temp
result.append(max)
return result[number]