并查集

并查集

1. 并查集的原理

原理

• 并查集支持的操作：（1）将两个集合合并；（2）查询两个元素是否在同一个集合中。

代码模板

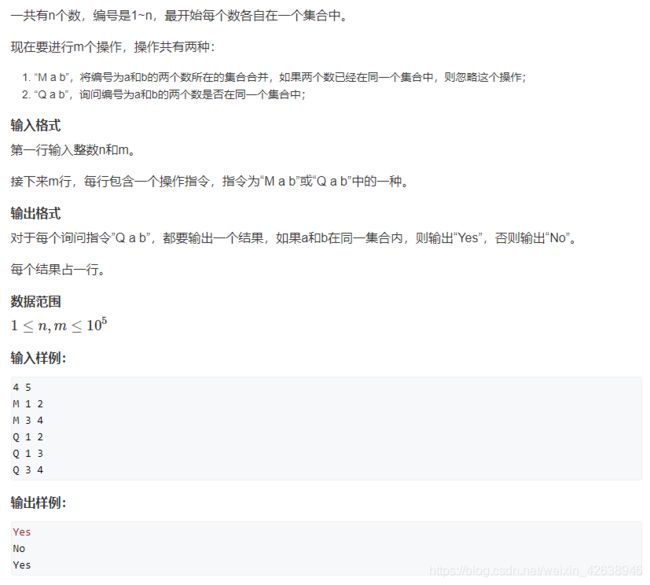
• AcWing 836. 合并集合

• C++

#include 

using namespace std;

const int N = 100010;

int p[N];

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);  // 路径压缩
    return p[x];
}

int main() {
     
    
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) p[i] = i;  // 并查集初始化
    
    while (m--) {
     
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if (*op == 'M') p[find(a)] = find(b);
        else {
     
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

2. AcWing上的并查集题目

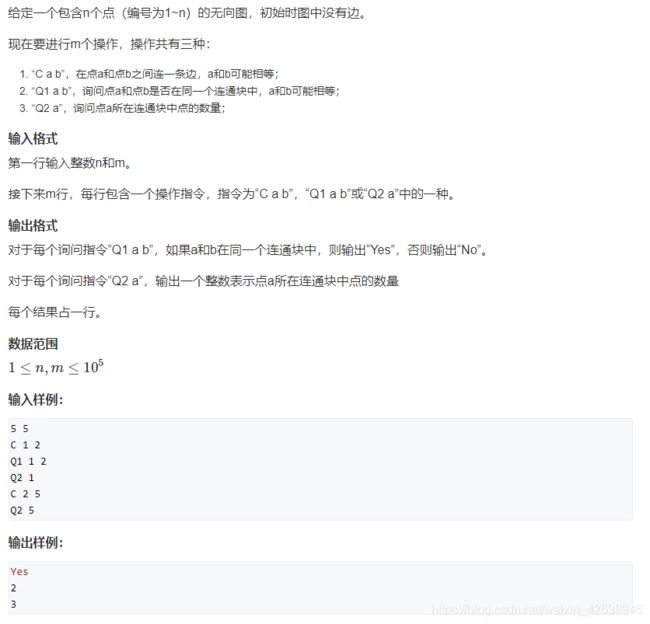
AcWing 837. 连通块中点的数量

问题描述

• 问题链接：AcWing 837. 连通块中点的数量

  

分析

• 在之前并查集的基础上，新开一个数组cnt，cnt[root]表示以root为根节点的集合数量

代码

#include 

using namespace std;

const int N = 100010;

int p[N], cnt[N];

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
     
    
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) p[i] = i, cnt[i] = 1;  // 初始化
    
    while (m--) {
     
        
        string op;
        int a, b;
        cin >> op;
        
        if (op == "C") {
     
            cin >> a >> b;
            a = find(a), b = find(b);
            if (a != b) {
     
                p[a] = b;
                cnt[b] += cnt[a];
            }
        } else if (op == "Q1") {
     
            cin >> a >> b;
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        } else {
     
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }
    
    return 0;
}

AcWing 240. 食物链

问题描述

• 问题链接：AcWing 240. 食物链

  

分析

代码

#include 

using namespace std;

const int N = 50010;

int p[N], d[N];  // d[i]表示i到p[i]的距离，初始为0

int find(int x) {
     
    if (p[x] != x) {
       // 如果p[x]不是根节点，执行该函数后p[x]就是根节点
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main() {
     
    
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) p[i] = i;
    
    int res = 0;
    while (m--) {
     
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);
        if (x > n || y > n) res++;
        else {
     
            int px = find(x), py = find(y);
            if (t == 1) {
       // 表示x和y是同类
                if (px == py && (d[x] - d[y]) % 3) res++;
                else if (px != py) {
       // x和y不在同一个集合中
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            } else {
       // 表示x吃y
                // 如果合法的话，d[x]一定比d[y]大
                if (px == py && (d[x] - d[y] - 1) % 3) res++;
                else if (px != py) {
     
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    printf("%d\n", res);
    
    return 0;
}

AcWing 1250. 格子游戏

问题描述

• 问题链接：AcWing 1250. 格子游戏

  

分析

• 将二维坐标转化为一维，然后判断是否存在两个点在同一个并查集中即可

代码

#include 

using namespace std;

const int N = 40010;

int n, m;
int p[N];

// 将二维坐标转化为一维，要求从左上角为(0, 0)
int get(int x, int y) {
     
    return x * n + y;
}

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
     
    
    cin >> n >> m;
    
    for (int i = 0; i < n * n; i++) p[i] = i;
    
    int res = 0;
    for (int i = 1; i <= m; i++) {
     
        int x, y;
        char d;
        cin >> x >> y >> d;
        x--, y--;
        int a = get(x, y);
        int b;
        if (d == 'D') b = get(x + 1, y);
        else b = get(x, y + 1);
        
        int pa = find(a), pb = find(b);
        if (pa == pb) {
     
            res = i;
            break;
        }
        p[pa] = pb;
    }
    
    if (!res) puts("draw");
    else cout << res << endl;
    
    return 0;
}

AcWing 1252. 搭配购买

问题描述

• 问题链接：AcWing 1252. 搭配购买

  

分析

• 题目要求，如果买一个物品，则与其相关的所有物品必须全部买下来（无向图，不是有依赖的背包问题）。我们可以找出所有的连通块，每个连通块看成一个物品，然后采用01背包模型就可以解决这个问题。
• 01背包可以参考：背包问题（背包九讲）

代码

#include 

using namespace std;

const int N = 10010;

int n, m, vol;
int v[N], w[N];
int p[N];
int f[N];

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
     
    
    cin >> n >> m >> vol;
    
    for (int i = 1; i <= n; i++) p[i] = i;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    while (m--) {
     
        int a, b;
        cin >> a >> b;
        int pa = find(a), pb = find(b);
        if (pa != pb) {
     
            v[pb] += v[pa];
            w[pb] += w[pa];
            p[pa] = pb;
        }
    }
    
    // 01背包
    for (int i = 1; i <= n; i++)
        if (p[i] == i)  // 并查集的根节点代表这个连通块合并成的物品
            for (int j = vol; j >= v[i]; j--)
                f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    cout << f[vol] << endl;
    return 0;
}

AcWing 237. 程序自动分析

问题描述

• 问题链接：AcWing 237. 程序自动分析

  

分析

代码

#include 
#include 

using namespace std;

const int N = 2000010;

int n, m;
int p[N];
unordered_map<int, int> S;  // 用于不保序的离散化

struct {
     
    int x, y, e;  // 原始输入的i,j和约束条件类型
} query[N];

int get(int x) {
     
    if (S.count(x) == 0) S[x] = ++n;
    return S[x];
}

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
     
    
    int T;
    scanf("%d", &T);
    while (T--) {
     
        n = 0;
        S.clear();
        scanf("%d", &m);
        for (int i = 0; i < m; i++) {
     
            int x, y, e;
            scanf("%d%d%d", &x, &y, &e);
            query[i] = {
     get(x), get(y), e};
        }
        
        for (int i = 1; i <= n; i++) p[i] = i;
        
        // 合并所有相等约束条件
        for (int i = 0; i < m; i++)
            if (query[i].e == 1) {
     
                int pa = find(query[i].x), pb = find(query[i].y);
                p[pa] = pb;
            }
        
        // 检查所有不等条件
        bool has_conflict = false;
        for (int i = 0; i < m; i++)
            if (query[i].e == 0) {
     
                int pa = find(query[i].x), pb = find(query[i].y);
                if (pa == pb) {
     
                    has_conflict = true;
                    break;
                }
            }
        
        if (has_conflict) puts("NO");
        else puts("YES");
    }
    
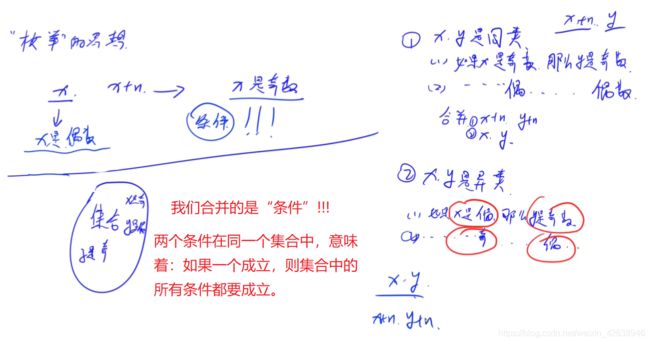
    return 0;
}

AcWing 239. 奇偶游戏

问题描述

• 问题链接：AcWing 239. 奇偶游戏

  

• 方法1：用带边权的并查集

分析

代码

#include 
#include 

using namespace std;

const int N = 20010;

int n, m;
int p[N], d[N];
unordered_map<int, int> S;

int get(int x) {
     
    if (S.count(x) == 0) S[x] = ++n;
    return S[x];
}

int find(int x) {
     
    if (p[x] != x) {
     
        int root = find(p[x]);
        d[x] = d[x] ^ d[p[x]];
        p[x] = root;
    }
    return p[x];
}

int main() {
     
    
    cin >> n >> m;
    n = 0;
    for (int i = 0; i < N; i++) p[i] = i;
    
    int res = m;
    for (int i = 1; i <= m; i++) {
     
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b);
        
        int t = 0;
        if (type == "odd") t = 1;
        
        int pa = find(a), pb = find(b);
        if (pa == pb) {
       // 说明a和b在同一个集合中
            if ((d[a] ^ d[b]) != t) {
     
                res = i - 1;
                break;
            }
        } else {
     
            p[pa] = pb;
            d[pa] = d[a] ^ d[b] ^ t;
        }
    }
    
    cout << res << endl;
    
    return 0;
}

也可以采用下面的写法（d[x]存储x到父节点的距离，类似于食物链的做法）：

#include 
#include 

using namespace std;

const int N = 20010;

int n, m;
int p[N], d[N];
unordered_map<int, int> S;

int get(int x) {
     
    if (S.count(x) == 0) S[x] = ++n;
    return S[x];
}

int find(int x) {
     
    if (p[x] != x) {
     
        int root = find(p[x]);
        d[x] += d[p[x]];  // 可能会导致溢出
        p[x] = root;
    }
    return p[x];
}

int main() {
     
    
    cin >> n >> m;
    n = 0;
    for (int i = 0; i < N; i++) p[i] = i;
    
    int res = m;
    for (int i = 1; i <= m; i++) {
     
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b);
        
        int t = 0;
        if (type == "odd") t = 1;
        
        int pa = find(a), pb = find(b);
        if (pa == pb) {
       // 说明a和b在同一个集合中
            if (((d[a] + d[b]) % 2 + 2) % 2 != t) {
       // 必须保证余数为负，也可以处理
                res = i - 1;
                break;
            }
        } else {
     
            p[pa] = pb;
            d[pa] = d[a] + d[b] + t;
        }
    }
    
    cout << res << endl;
    
    return 0;
}

---

• 方法2：带扩展域的并查集

分析

代码

#include 
#include 

using namespace std;

const int N = 40010, Base = N / 2;

int n, m;
int p[N], d[N];
unordered_map<int, int> S;

int get(int x) {
     
    if (S.count(x) == 0) S[x] = ++n;
    return S[x];
}

int find(int x) {
     
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
     
    
    cin >> n >> m;
    n = 0;
    for (int i = 0; i < N; i++) p[i] = i;
    
    int res = m;
    for (int i = 1; i <= m; i++) {
     
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b);
        
        if (type == "even") {
     
            if (find(a + Base) == find(b)) {
     
                // 此时题目输入为a,b是同类，但是发现a,b是异类，矛盾
                res = i - 1;
                break;
            }
            p[find(a)] = find(b);
            p[find(a + Base)] = find(b + Base);
        } else {
     
            if (find(a) == find(b)) {
     
                // 此时题目输入为a,b是异类，但是发现a,b是同类，矛盾
                res = i - 1;
                break;
            }
            p[find(a + Base)] = p[find(b)];
            p[find(a)] = p[find(b + Base)];
        }
    }
    
    cout << res << endl;
    
    return 0;
}

AcWing 238. 银河英雄传说

问题描述

• 问题链接：AcWing 238. 银河英雄传说

  

分析

代码

#include 

using namespace std;

const int N = 30010;

int m;
// s存储集合中元素的个数，p[x]表示x到p[x]的距离
int p[N], s[N], d[N];

int find(int x) {
     
    if (p[x] != x) {
     
        int root = find(p[x]);
        d[x] += d[p[x]];
        p[x] = root;
    }
    return p[x];
}

int main() {
     
    
    scanf("%d", &m);
    
    for (int i = 0; i < N; i++) {
     
        p[i] = i;
        s[i] = 1;
        // d默认全为0，不需要初始化了
    }
    
    while (m--) {
     
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if (op[0] == 'M') {
     
            int pa = find(a), pb = find(b);
            d[pa] = s[pb];
            s[pb] += s[pa];
            p[pa] = pb;
        } else {
     
            int pa = find(a), pb = find(b);
            if (pa != pb) puts("-1");
            else printf("%d\n", max(0, abs(d[a] - d[b]) - 1));
        }
    }
    
    return 0;
}

3. 力扣上的并查集题目

• Leetcode 0547 省份数量 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0684 冗余连接 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0685 冗余连接 II ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0721 账户合并 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0765 情侣牵手 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0803 打砖块 ----> 题目链接 ----> 我的解答：Java、C++ (逆向思维)
• Leetcode 0839 相似的字符串 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0947 移除最多的同行或同列石头 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0959 由斜杠划分区域 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 0990 等式方程的可满足性 ----> 题目链接 ----> 我的解答：Java、C++
• LeetCode 1202 交换字符串中的元素 ----> 题目链接 ----> 我的解答：Java、C++
• Leetcode 1319 联通网络的操作次数 ----> 题目链接 ----> 我的解答：Java、C++
• LeetCode 1579 保证图可完全遍历 ----> 题目链接 ----> 我的解答：Java、C++