【现代控制理论基础】一、线性系统的状态空间描述
Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: AXYZdong的博客
B站主页为:AXYZdong的个人主页
文章目录
-
- 1.1 状态空间分析法
- 1.2 状态结构图
- 1.3 状态空间描述的建立
-
- 1.3.1 由系统框图建立空间状态描述
- 1.3.2 由系统机理建立空间状态描述
- 1.4 化输入-输出描述为状态空间描述及其几种标准形式
-
- 1.4.1 传递函数没有零点的实现
- 1.4.2 传递函数有零点的实现
- 1.5 由状态空间表达式求传递函数阵
- 1.6 状态矢量的线性变换
-
- 1.6.1 系统状态空间表达式的非唯一性
- 1.6.2 系统特征值的不变性及系统的不变量
- 1.6.3 状态空间表达式变换为约旦标准型
- 参考文献
1.1 状态空间分析法
- 状态变量
一 组 变 量 → { 1 、 足 以 完 全 确 定 系 统 运 动 状 态 2 、 个 数 又 是 最 小 一组变量 \to \begin{cases} 1、足以完全确定系统运动状态 \\ 2、个数又是最小 \end{cases} 一组变量→{ 1、足以完全确定系统运动状态2、个数又是最小
性 质 : { 1 、 x t = t 0 2 、 t ≥ t 0 时 刻 的 输 入 I t → 完 全 确 定 在 任 何 t ≥ t 0 时 刻 的 状 态 x t 性质: \begin{cases} 1、x_{t=t_0} \\ 2、t \geq t_0 时刻的输入I_t \end{cases} \to完全确定在任何t \geq t_0 时刻的状态 x_t 性质:{ 1、xt=t02、t≥t0时刻的输入It→完全确定在任何t≥t0时刻的状态xt
类似于函数: x t = f ( x t 0 , I t ) x_t=f(x_{t_0},I_t) xt=f(xt0,It) - 状态矢量
如果 n n n 个状态变量用 x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) x_1(t),x_2(t),...,x_n(t) x1(t),x2(t),...,xn(t) 表示,并把这些状态变量看作是矢量 x ( t ) x(t) x(t) 的分量,则称 x ( t ) x(t) x(t)为状态矢量,记作:
x ( t ) = ( x 1 ( t ) x 2 ( t ) ⋮ x n ( t ) ) x(t)=\begin{pmatrix} x_1(t) \\ x_2(t)\\ \vdots \\ x_n(t) \\ \end{pmatrix} x(t)=⎝⎜⎜⎜⎛x1(t)x2(t)⋮xn(t)⎠⎟⎟⎟⎞ - 状态空间
以状态变量用 x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) x_1(t),x_2(t),...,x_n(t) x1(t),x2(t),...,xn(t) 为坐标轴所构成的 n n n 维空间,称为状态空间。 - 状态方程
由系统的状态变量构成的一阶微分方程组称为系统的状态空间。
例:以 R − L − C R-L-C R−L−C 电路说明如何用状态变量描述系统

▲ 图1
有 一 阶 微 分 方 程 组 : { C ⋅ d u c d t = i L ⋅ d i d t + R i + u c = u ⟹ { u ˊ c = 1 C ⋅ i i ˊ = − 1 L u c − R L i + 1 L u (1) 有一阶微分方程组: \begin{cases} C\cdot\frac{du_c}{dt}=i \\[2ex] L\cdot\frac{di}{dt}+Ri+u_c=u \end{cases} \implies \begin{cases} \acute{u}_c=\frac{1}{C}\cdot i \\[2ex] \acute{i}=-\frac{1}{L}u_c-\frac{R}{L}i+\frac{1}{L}u \end{cases} \tag1 有一阶微分方程组:⎩⎨⎧C⋅dtduc=iL⋅dtdi+Ri+uc=u⟹⎩⎨⎧uˊc=C1⋅iiˊ=−L1uc−LRi+L1u(1)
令 { x 1 = u c x 2 = i ⟹ ( x 1 ˊ x 2 ˊ ) = ( 0 1 C − 1 L − R L ) ( x 1 x 2 ) + ( 0 1 L ) u (2) 令 \begin{cases} x_1=u_c \\[2ex] x_2=i \end{cases} \implies \begin{pmatrix} \acute{x_1}\\[2ex] \acute{x_2}\\ \end{pmatrix} = \begin{pmatrix} 0 & \large\frac{1}{C}\\[2ex] \large-\frac{1}{L} & \large-\frac{R}{L}\\ \end{pmatrix} \begin{pmatrix} x_1\\[2ex] x_2\\ \end{pmatrix} + \begin{pmatrix} 0\\[2ex] \large\frac{1}{L}\\ \end{pmatrix}u \tag2 令⎩⎨⎧x1=ucx2=i⟹(x1ˊx2ˊ)=⎝⎛0−L1C1−LR⎠⎞(x1x2)+⎝⎛0L1⎠⎞u(2)
或 : x ˊ = A x + b u 或 : \acute{x}=Ax+bu 或:xˊ=Ax+bu
其 中 : x ˊ = ( x 1 ˊ x 2 ˊ ) , A = ( 0 1 C − 1 L − R L ) , b = ( 0 1 L ) 其中:\acute{x}= \begin{pmatrix} \acute{x_1}\\[2ex] \acute{x_2}\\ \end{pmatrix}, A= \begin{pmatrix} 0 & \large\frac{1}{C}\\[2ex] \large-\frac{1}{L} & \large-\frac{R}{L}\\ \end{pmatrix}, b= \begin{pmatrix} 0\\[2ex] \large\frac{1}{L}\\ \end{pmatrix} 其中:xˊ=(x1ˊx2ˊ),A=⎝⎛0−L1C1−LR⎠⎞,b=⎝⎛0L1⎠⎞
上述(1)和(2)式分别为图1中系统的 状态方程 和 状态方程的矩阵表达形式。
- 输出方程
在指定系统输出的情况下,该输出与状态变量间的函数关系式,称为系统的输出方程。
在例中系统中,若指定 x 1 = u c x_1=u_c x1=uc ,则输出方程 y = u c y=u_c y=uc 或 : y = x 1 (3) 或: y=x_1\tag3 或:y=x1(3)
矩阵表示形式:
y = ( 1 , 0 ) ( x 1 x 2 ) (4) y= \begin{pmatrix} 1,0 \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix}\tag4 y=(1,0)(x1x2)(4) - 状态空间表达式
状态方程和输出方程总合起来,构成对一个系统完整的动态描述称为系统的状态空间表达式。
如式(1)和式(3)所示,而式(2)和式(4)就是图1系统的状态空间表达式。 - 单输入——单输出定常系统,矢量矩阵表示时的状态空间表达式为:
x ˊ = A x + b u y = c x (5) \acute{x}=Ax+bu\\ y=cx \tag5 xˊ=Ax+buy=cx(5)
式中, x = ( x 1 x 2 ⋮ x n ) 为 n 维 状 态 矢 量 ; A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ) 为 系 统 内 部 状 态 的 联 系 , 称 为 系 统 矩 阵 , 为 n × n 方 阵 ; b = ( b 1 b 2 ⋮ b n ) 为 输 入 对 状 态 的 作 用 , 称 为 输 入 矩 阵 或 控 制 矩 阵 , 这 里 为 n × 1 的 列 阵 ; c = ( c 1 , c 2 , . . . , c n ) 为 输 出 矩 阵 , 这 里 为 1 × n 的 行 阵 。 x=\begin{pmatrix} x_1 \\ x_2\\ \vdots \\ x_n \\ \end{pmatrix} 为 n 维状态矢量;\\[3ex] A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{pmatrix}为系统内部状态的联系,称为系统矩阵,为n\times n方阵; \\[3ex] b=\begin{pmatrix} b_1 \\ b_2\\ \vdots \\ b_n \\ \end{pmatrix} 为输入对状态的作用,称为输入矩阵或控制矩阵,这里为n\times 1的列阵; \\[3ex] c=\begin{pmatrix} c_1 , c_2 ,...,c_n \\ \end{pmatrix} 为输出矩阵,这里为1\times n的行阵。 x=⎝⎜⎜⎜⎛x1x2⋮xn⎠⎟⎟⎟⎞为n维状态矢量;A=⎝⎜⎜⎜⎛a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎠⎟⎟⎟⎞为系统内部状态的联系,称为系统矩阵,为n×n方阵;b=⎝⎜⎜⎜⎛b1b2⋮bn⎠⎟⎟⎟⎞为输入对状态的作用,称为输入矩阵或控制矩阵,这里为n×1的列阵;c=(c1,c2,...,cn)为输出矩阵,这里为1×n的行阵。 - 多输入——多输出定常系统,矢量矩阵表示时的状态空间表达式为:
x ˊ = A x + B u y = C x + D u (6) \acute{x}=Ax+Bu\\ y=Cx+Du\tag6 xˊ=Ax+Buy=Cx+Du(6)
式 中 , x 和 A 同 单 输 入 系 统 , 分 别 n 维 状 态 矢 量 和 n × n 系 统 矩 阵 式中,x和 A同单输入系统,分别n维状态矢量和n\times n系统矩阵 式中,x和A同单输入系统,分别n维状态矢量和n×n系统矩阵
u = ( u 1 u 2 ⋮ u r ) 为 r 维 输 入 矢 量 ; y = ( y 1 y 2 ⋮ y m ) 为 m 维 输 出 矢 量 ; B = ( b 11 b 12 ⋯ b 1 r b 21 b 22 ⋯ b 2 r ⋮ ⋮ ⋱ ⋮ b n 1 b n 2 ⋯ b n r ) 为 n × r 输 入 矩 阵 ; C = ( c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋮ ⋮ ⋱ ⋮ c m 1 c m 2 ⋯ c m n ) 为 m × n 输 出 矩 阵 ; D = ( d 11 d 12 ⋯ d 1 r d 21 d 22 ⋯ d 2 r ⋮ ⋮ ⋱ ⋮ d m 1 d m 2 ⋯ d m r ) 为 m × r 直 接 传 递 矩 阵 。 为 了 简 便 , 一 般 不 考 虑 输 入 矢 量 的 直 接 传 递 , 即 令 D = 0 u=\begin{pmatrix} u_1 \\ u_2\\ \vdots \\ u_r \\ \end{pmatrix} 为 r 维输入矢量; y=\begin{pmatrix} y_1 \\ y_2\\ \vdots \\ y_m \\ \end{pmatrix} 为 m 维输出矢量;\\[3ex] B=\begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1r} \\ b_{21} & b_{22} & \cdots & b_{2r} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nr} \\ \end{pmatrix}为n\times r输入矩阵;\\[3ex] C=\begin{pmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{m1} & c_{m2} & \cdots & c_{mn} \\ \end{pmatrix}为m\times n输出矩阵; \\[3ex] D=\begin{pmatrix} d_{11} & d_{12} & \cdots & d_{1r} \\ d_{21} & d_{22} & \cdots & d_{2r} \\ \vdots & \vdots & \ddots & \vdots \\ d_{m1} & d_{m2} & \cdots & d_{mr} \\ \end{pmatrix}为m\times r直接传递矩阵。\\[2ex] 为了简便,一般不考虑输入矢量的直接传递,即令D=0 u=⎝⎜⎜⎜⎛u1u2⋮ur⎠⎟⎟⎟⎞为r维输入矢量;y=⎝⎜⎜⎜⎛y1y2⋮ym⎠⎟⎟⎟⎞为m维输出矢量;B=⎝⎜⎜⎜⎛b11b21⋮bn1b12b22⋮bn2⋯⋯⋱⋯b1rb2r⋮bnr⎠⎟⎟⎟⎞为n×r输入矩阵;C=⎝⎜⎜⎜⎛c11c21⋮cm1c12c22⋮cm2⋯⋯⋱⋯c1nc2n⋮cmn⎠⎟⎟⎟⎞为m×n输出矩阵;D=⎝⎜⎜⎜⎛d11d21⋮dm1d12d22⋮dm2⋯⋯⋱⋯d1rd2r⋮dmr⎠⎟⎟⎟⎞为m×r直接传递矩阵。为了简便,一般不考虑输入矢量的直接传递,即令D=0 - 状态空间表达式的系统框图

▲ 式5框图
▲ 式6框图
1.2 状态结构图
状态空间描述的结构图绘图步骤:
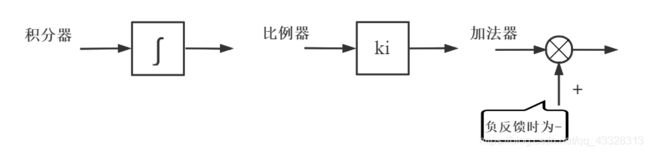
- 画出所有积分器;(积分器的个数等于状态变量的个数,每个积分器的输出表示相应的某个状态变量)
- 根据状态方程和输出方程,画出相应的加法器和比例器;
- 用箭头将这些器件按照一定的顺序连接起来。
例:一阶标量微分方程: x ˊ = a x + b u \acute{x}=ax+bu xˊ=ax+bu
▲ 一阶标量微分方程模拟结构图
已知状态空间表达式
x 1 ˊ = x 2 x 2 ˊ = x 3 x 3 ˊ = − 6 x 1 − 3 x 2 − 2 x 3 + u y = x 1 + x 2 \acute{x_1}=x_2\\ \acute{x_2}=x_3\\ \acute{x_3}=-6x_1-3x_2-2x_3+u\\ y=x_1+x_2 x1ˊ=x2x2ˊ=x3x3ˊ=−6x1−3x2−2x3+uy=x1+x2
则系统的模拟结构图为:
1.3 状态空间描述的建立
1.3.1 由系统框图建立空间状态描述
▲ a) 系统框图;b)系统模拟结构图
由图可知:
状 态 方 程 : { x 1 ˊ = K 3 T 3 x 2 x 2 ˊ = − 1 T 2 x 2 + K 2 T 2 x 3 x 3 ˊ = − 1 T 1 x 3 − K 1 K 4 T 1 x 1 + K 1 T 1 u 输 出 方 程 : y = x 1 状态方程: \begin{cases} \acute{x_1}=\frac{K_3}{T_3}x_2\\[2ex] \acute{x_2}=-\frac{1}{T_2}x_2+\frac{K_2}{T_2}x_3\\[2ex] \acute{x_3}=-\frac{1}{T_1}x_3-\frac{K_1K_4}{T_1}x_1+\frac{K_1}{T_1}u\\ \end{cases}\\[2ex] 输出方程:y=x_1 状态方程:⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x1ˊ=T3K3x2x2ˊ=−T21x2+T2K2x3x3ˊ=−T11x3−T1K1K4x1+T1K1u输出方程:y=x1
写成矢量矩阵形式:
x ˊ = ( 0 K 3 T 3 0 0 − 1 T 2 K 2 T 2 − K 1 K 4 T 1 0 − 1 T 1 ) x + ( 0 0 K 1 T 1 ) u y = ( 1 , 0 , 0 ) x 1 \acute{x} = \begin{pmatrix} 0 & \large\frac{K_3}{T_3} & 0\\[2ex] 0 & \large-\frac{1}{T_2} & \large\frac{K_2}{T_2}\\[2ex] \large-\frac{K_1K_4}{T_1} & 0 & \large-\frac{1}{T_1} \\ \end{pmatrix} x + \begin{pmatrix} 0\\[2ex] 0\\[2ex] \large\frac{K_1}{T_1}\\ \end{pmatrix}u \\[2ex] y= \begin{pmatrix} 1 , 0, 0 \end{pmatrix}x_1 xˊ=⎝⎜⎜⎜⎜⎛00−T1K1K4T3K3−T2100T2K2−T11⎠⎟⎟⎟⎟⎞x+⎝⎜⎜⎜⎛00T1K1⎠⎟⎟⎟⎞uy=(1,0,0)x1
注:带零点环节的处理方法
- 先展开部分分式
- 得到等效方块图
- 再变换成模拟结构图
s + z s + p = 1 + z − p s + p \frac{s+z}{s+p}=1+\frac{z-p}{s+p} s+ps+z=1+s+pz−p
1.3.2 由系统机理建立空间状态描述
步骤:
- 根据系统机理建立微分方程或者差分方程
- 选择有关的物理量作为状态变量
- 导出状态空间表达式
例:电网络如图所示,输入量为电流源,并指定电容 C 1 C_1 C1 和 C 2 C_2 C2 上的电压作为输出,求此网络的状态空间表达式。
解:从节点 a 、 b 、 c a、b、c a、b、c ,按基尔霍夫电流定律列出电流方程:
{ i + i 3 + i 1 − C 2 u c 2 ˊ = 0 C 1 u c 1 ˊ + i 1 + i 2 = 0 C 2 u c 2 ˊ + i 2 − i 4 = 0 \begin{cases} i+i_3+i_1-C_2\acute{u_{c2}}=0\\[2ex] C_1\acute{u_{c1}}+i_1+i_2=0\\[2ex] C_2\acute{u_{c2}}+i_2-i_4=0\\ \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧i+i3+i1−C2uc2ˊ=0C1uc1ˊ+i1+i2=0C2uc2ˊ+i2−i4=0
选取状态变量:
x = ( x 1 x 2 x 3 x 4 ) = ( u c 1 u c 2 i 1 i 2 ) x=\begin{pmatrix} x_1 \\ x_2\\ x_3 \\ x_4 \\ \end{pmatrix} = \begin{pmatrix} u_{c_1} \\ u_{c_2}\\ i_1 \\ i_2 \\ \end{pmatrix} x=⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞=⎝⎜⎜⎛uc1uc2i1i2⎠⎟⎟⎞
上述电流方程则变为:
{ i + i 3 + x 3 − C 2 x 2 ˊ = 0 C 1 x 1 ˊ + x 3 + x 4 = 0 C 2 x 2 ˊ + x 4 − i 4 = 0 (7) \begin{cases} i+i_3+x_3-C_2\acute{x_2}=0\\[2ex] C_1\acute{x_1}+x_3+x_4=0\\[2ex] C_2\acute{x_2}+x_4-i_4=0\\ \end{cases}\tag7 ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧i+i3+x3−C2x2ˊ=0C1x1ˊ+x3+x4=0C2x2ˊ+x4−i4=0(7)
从回路 l 1 、 l 2 、 l 3 l_1、l_2、l_3 l1、l2、l3 ,按基尔霍夫电压定律列出电压方程:
{ − L 1 x 3 ˊ + x 1 + R 1 i 3 = 0 − x 1 + L 2 x 4 ˊ + R 2 i 4 = 0 x 2 − L 2 x 4 ˊ + L 1 x 3 ˊ = 0 (8) \begin{cases} -L_1\acute{x_3}+x_1+R_1i_3=0\\[2ex] -x_1+L_2\acute{x_4}+R_2i_4=0\\[2ex] x_2-L_2\acute{x_4}+L_1\acute{x_3}=0\\ \end{cases}\tag8 ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧−L1x3ˊ+x1+R1i3=0−x1+L2x4ˊ+R2i4=0x2−L2x4ˊ+L1x3ˊ=0(8)
(7)和(8)式联立消去独立变量 i 3 、 i 4 i_3、i_4 i3、i4 得:
{ x 1 ˊ = − 1 C 1 x 3 − 1 C 1 x 4 R 1 C 2 x 2 ˊ − L 1 x 3 ˊ = − x 1 + R 1 x 3 + R 1 i R 2 C 2 x 2 ˊ + L 2 x 4 ˊ = x 1 − R 2 x 4 − L x 3 ˊ + L 2 x 4 ˊ = x 2 (9) \begin{cases} \acute{x_1}=-\frac{1}{C_1}x_3-\frac{1}{C_1}x_4\\[2ex] R_1C_2\acute{x_2}-L_1\acute{x_3}=-x_1+R_1x_3+R_1i\\[2ex] R_2C_2\acute{x_2}+L_2\acute{x_4}=x_1-R_2x_4\\[2ex] -L\acute{x_3}+L_2\acute{x_4}=x_2 \end{cases}\tag9 ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧x1ˊ=−C11x3−C11x4R1C2x2ˊ−L1x3ˊ=−x1+R1x3+R1iR2C2x2ˊ+L2x4ˊ=x1−R2x4−Lx3ˊ+L2x4ˊ=x2(9)
(9)式解出 x 1 ˊ 、 x 2 ˊ 、 x 3 ˊ 、 x 4 ˊ \acute{x_1}、\acute{x_2}、\acute{x_3}、\acute{x_4} x1ˊ、x2ˊ、x3ˊ、x4ˊ,得到状态空间表达式:
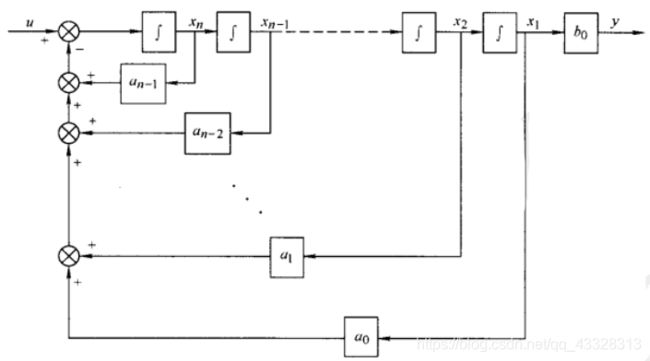
1.4 化输入-输出描述为状态空间描述及其几种标准形式
1.4.1 传递函数没有零点的实现
系统微分方程为:
y ( n ) + a n − 1 y ( n − 1 ) + . . . + a 1 y ˊ + a 0 y = b 0 u ( t ) y^{(n)}+a_{n-1}y^{(n-1)}+...+a_1\acute{y}+a_0y=b_0u(t) y(n)+an−1y(n−1)+...+a1yˊ+a0y=b0u(t)
相应系统传递函数:
W ( s ) = b 0 s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 W(s)=\frac{b_0}{s^n+a_{n-1}s^{n-1}+...+a_1s+a_0} W(s)=sn+an−1sn−1+...+a1s+a0b0
可选取一组状态变量:
x 1 ˊ = x 2 x 2 ˊ = x 3 ⋮ x n − 1 ˊ = x n x n ˊ = − a 0 x 1 − a 1 x 2 − . . . − a n − 2 x n − 1 − a n − 1 x n + u \acute{x_1}=x_2\\[2ex] \acute{x_2}=x_3\\ \vdots \\ \acute{x_{n-1}}=x_n\\[2ex] \acute{x_n}=-a_0x_1-a_1x_2-...-a_{n-2}x_{n-1}-a_{n-1}x_n+u x1ˊ=x2x2ˊ=x3⋮xn−1ˊ=xnxnˊ=−a0x1−a1x2−...−an−2xn−1−an−1xn+u
输出方程: y = b 0 x 1 y=b_0x_1 y=b0x1
表示成矩阵形式:
( x 1 ˊ x 2 ˊ ⋮ x n − 1 ˊ x n ˊ ) = ( 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 − a 0 − a 1 − a 2 ⋯ − a n − 1 ) ( x 1 x 2 ⋮ x n − 1 x n ) + ( 0 0 ⋮ 0 1 ) u (10) \begin{pmatrix} \acute{x_1} \\[2ex] \acute{x_2}\\[2ex] \vdots \\[2ex] \acute{x_{n-1}} \\[2ex] \acute{x_n} \\ \end{pmatrix} =\begin{pmatrix} 0 & 1 & 0 &\cdots & 0 \\[2ex] 0 & 0 & 1 &\cdots & 0 \\[2ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[2ex] 0 & 0 & 0 &\cdots & 1 \\[2ex] -a_{0} & -a_{1} & -a_2 & \cdots & -a_{n-1} \\ \end{pmatrix} \begin{pmatrix} x_1 \\[2ex] x_2\\[2ex] \vdots \\[2ex] x_{n-1}\\[2ex] x_n \\ \end{pmatrix} + \begin{pmatrix} 0 \\[2ex] 0\\[2ex] \vdots \\[2ex] 0\\[2ex] 1 \\ \end{pmatrix}u\tag{10} ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1ˊx2ˊ⋮xn−1ˊxnˊ⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞u(10)
x ˊ = A x + b u y = ( b 0 , 0 , 0 , ⋯ , 0 ) x 1 \acute{x}=Ax+bu\\[2ex] y=\begin{pmatrix} b_0,0 , 0,\cdots, 0 \end{pmatrix}x_1 \\[2ex] xˊ=Ax+buy=(b0,0,0,⋯,0)x1
当 矩 阵 A 具 有 A = ( 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 − a 0 − a 1 − a 2 ⋯ − a n − 1 ) 时 , 称 为 友 矩 阵 。 当矩阵 A 具有A=\begin{pmatrix} 0 & 1 & 0 &\cdots & 0 \\[2ex] 0 & 0 & 1 &\cdots & 0 \\[2ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[2ex] 0 & 0 & 0 &\cdots & 1 \\[2ex] -a_{0} & -a_{1} & -a_2 & \cdots & -a_{n-1} \\ \end{pmatrix}时,称为友矩阵。 当矩阵A具有A=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞时,称为友矩阵。
友矩阵的特点为:
- 主对角线上方元素均为1
- 最后一行的元素可去任意值
- 其余元素均为0
▲ 系统模拟结构图
1.4.2 传递函数有零点的实现
系统微分方程为:
y ( n ) + a n − 1 y ( n − 1 ) + . . . + a 1 y ˊ + a 0 y = b m u ( m ) + b m − 1 u ( m − 1 ) + . . . + b 1 u + ˊ b 0 u y^{(n)}+a_{n-1}y^{(n-1)}+...+a_1\acute{y}+a_0y=b_mu^{(m)}+b_{m-1}u^{(m-1)}+...+b_1\acute{u+}b_0u y(n)+an−1y(n−1)+...+a1yˊ+a0y=bmu(m)+bm−1u(m−1)+...+b1u+ˊb0u
相应系统传递函数:
W ( s ) = b m s m + b m − 1 s m − 1 + . . . + b 1 s + b 0 s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 , m ≤ n W(s)=\frac{b_ms^m+b_{m-1}s^{m-1}+...+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_1s+a_0},m\leq n W(s)=sn+an−1sn−1+...+a1s+a0bmsm+bm−1sm−1+...+b1s+b0,m≤n
在这种包含有输人函数导数情况下的实现问题,与前述实现的不同点主要在于选取合适的结构,使得状态方程中不包含输入函数的导数项,否则将给求解和物理实现带来麻烦。
为了说明方便,又不失一般性,这里先从三阶微分方程出发,找出其实现规律,然后推广到 n 阶系统。
设系统传递函数:
W ( s ) = Y ( s ) U ( s ) = b 3 s 3 + b 2 s 2 + b 1 s + b 0 s 3 + a 2 s 2 + a 1 s + a 0 , m = n = 3 W(s)=\frac{Y(s)}{U(s)}=\frac{b_3s^3+b_{2}s^{2}+b_1s+b_0}{s^3+a_{2}s^{2} +a_1s+a_0},m=n=3 W(s)=U(s)Y(s)=s3+a2s2+a1s+a0b3s3+b2s2+b1s+b0,m=n=3
上式可变换为:
W ( s ) = b 3 + ( b 2 − a 2 b 3 ) s 2 + ( b 1 − a 1 b 3 ) s + ( b 0 − a 0 b 3 ) s 3 + a 2 s 2 + a 1 s + a 0 , m = n = 3 令 : Y 1 ( s ) = 1 s 3 + a 2 s 2 + a 1 s + a 0 U ( s ) 则 : Y ( s ) = b 3 U ( s ) + Y 1 ( s ) [ ( b 2 − a 2 b 3 ) s 2 + ( b 1 − a 1 b 3 ) s + ( b 0 − a 0 b 3 ) ] 对 上 式 求 拉 式 反 变 换 , 可 得 : y = b 3 u + ( b 2 − a 2 b 3 ) y 1 ( 2 ) + ( b 1 − a 1 b 3 ) y 1 ˊ + ( b 0 − a 0 b 3 ) y 1 W(s)=b_3+\frac{(b_2-a_2b_3)s^2+(b_1-a_1b_3)s+(b_0-a_0b_3)}{s^3+a_{2}s^{2} +a_1s+a_0},m=n=3\\[3ex] 令:Y_1(s)=\frac{1}{s^3+a_{2}s^{2} +a_1s+a_0}U(s)\\[2ex] 则:Y(s)=b_3U(s)+Y_1(s)[(b_2-a_2b_3)s^2+(b_1-a_1b_3)s+(b_0-a_0b_3)]\\[2ex] 对上式求拉式反变换,可得:\\[2ex] y=b_3u+(b_2-a_2b_3)y^{(2)}_1+(b_1-a_1b_3)\acute{y_1}+(b_0-a_0b_3)y_1 W(s)=b3+s3+a2s2+a1s+a0(b2−a2b3)s2+(b1−a1b3)s+(b0−a0b3),m=n=3令:Y1(s)=s3+a2s2+a1s+a01U(s)则:Y(s)=b3U(s)+Y1(s)[(b2−a2b3)s2+(b1−a1b3)s+(b0−a0b3)]对上式求拉式反变换,可得:y=b3u+(b2−a2b3)y1(2)+(b1−a1b3)y1ˊ+(b0−a0b3)y1
可得系统模拟结构图:

▲ 系统模拟结构图
选取状态变量:
x 1 ˊ = x 2 x 2 ˊ = x 3 x 3 ˊ = − a 0 x 1 − a 1 x 2 − a 2 x 3 + u y = b 3 u + ( b 2 − a 2 b 3 ) x 3 + ( b 1 − a 1 b 3 ) x 2 + ( b 0 − a 0 b 3 ) x 1 \acute{x_1}=x_2\\[2ex] \acute{x_2}=x_3\\[2ex] \acute{x_3}=-a_0x_1-a_1x_2-a_{2}x_{3}+u\\[2ex] y=b_3u+(b_2-a_2b_3)x_3+(b_1-a_1b_3)x_2+(b_0-a_0b_3)x_1 x1ˊ=x2x2ˊ=x3x3ˊ=−a0x1−a1x2−a2x3+uy=b3u+(b2−a2b3)x3+(b1−a1b3)x2+(b0−a0b3)x1
表示成矩阵形式:
( x 1 ˊ x 2 ˊ x 3 ˊ ) = ( 0 1 0 0 0 1 − a 0 − a 1 − a 2 ) ( x 1 x 2 x 3 ) + ( 0 0 1 ) u (10) \begin{pmatrix} \acute{x_1} \\[2ex] \acute{x_2}\\[2ex] \acute{x_3} \\ \end{pmatrix} =\begin{pmatrix} 0 & 1 & 0 \\[2ex] 0 & 0 & 1 \\[2ex] -a_{0} & -a_{1} & -a_2 \\ \end{pmatrix} \begin{pmatrix} x_1 \\[2ex] x_2\\[2ex] x_3 \\ \end{pmatrix} + \begin{pmatrix} 0 \\[2ex] 0\\[2ex] 1 \\ \end{pmatrix}u\tag{10} ⎝⎜⎜⎜⎛x1ˊx2ˊx3ˊ⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛00−a010−a101−a2⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛x1x2x3⎠⎟⎟⎟⎞+⎝⎜⎜⎜⎛001⎠⎟⎟⎟⎞u(10)
y = ( ( b 0 − a 0 b 3 ) , ( b 1 − a 1 b 3 ) , ( b 2 − a 2 b 3 ) ) ( x 1 x 2 x 3 ) + b 3 u y=\begin{pmatrix} (b_0-a_0b_3),(b_1-a_1b_3),(b_2-a_2b_3) \end{pmatrix}\begin{pmatrix} x_1 \\[2ex] x_2\\[2ex] x_3 \\ \end{pmatrix}+b_3u \\[2ex] y=((b0−a0b3),(b1−a1b3),(b2−a2b3))⎝⎜⎜⎜⎛x1x2x3⎠⎟⎟⎟⎞+b3u
推广到 n 阶系统
( x 1 ˊ x 2 ˊ ⋮ x n − 1 ˊ x n ˊ ) = ( 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 − a 0 − a 1 − a 2 ⋯ − a n − 1 ) ( x 1 x 2 ⋮ x n − 1 x n ) + ( 0 0 ⋮ 0 1 ) u y = ( ( b 0 − a 0 b n ) , ( b 1 − a 1 b n ) , . . . , ( b n − 1 − a n − 1 b n ) ) ( x 1 x 2 ⋮ x n − 1 x n ) + b n u \begin{pmatrix} \acute{x_1} \\[2ex] \acute{x_2}\\[2ex] \vdots \\[2ex] \acute{x_{n-1}} \\[2ex] \acute{x_n} \\ \end{pmatrix} =\begin{pmatrix} 0 & 1 & 0 &\cdots & 0 \\[2ex] 0 & 0 & 1 &\cdots & 0 \\[2ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[2ex] 0 & 0 & 0 &\cdots & 1 \\[2ex] -a_{0} & -a_{1} & -a_2 & \cdots & -a_{n-1} \\ \end{pmatrix} \begin{pmatrix} x_1 \\[2ex] x_2\\[2ex] \vdots \\[2ex] x_{n-1}\\[2ex] x_n \\ \end{pmatrix} + \begin{pmatrix} 0 \\[2ex] 0\\[2ex] \vdots \\[2ex] 0\\[2ex] 1 \\ \end{pmatrix}u\\[3ex] y=\begin{pmatrix} (b_0-a_0b_n),(b_1-a_1b_n),...,(b_{n-1}-a_{n-1}b_n) \end{pmatrix}\begin{pmatrix} x_1 \\ x_2\\ \vdots \\ x_{n-1}\\ x_n \\ \end{pmatrix}+b_nu \\[2ex] ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1ˊx2ˊ⋮xn−1ˊxnˊ⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞uy=((b0−a0bn),(b1−a1bn),...,(bn−1−an−1bn))⎝⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎞+bnu
1.5 由状态空间表达式求传递函数阵
状 态 空 间 描 述 : { x ˊ = A x + B u y = C x + D u 状态空间描述: \begin{cases} \acute{x}=Ax+Bu\\[2ex] y=Cx+Du \end{cases} 状态空间描述:⎩⎨⎧xˊ=Ax+Buy=Cx+Du
根据传递函数定义,对上式进行拉氏变换,并令 x ( 0 ) = x 0 = 0 x(0)=x_0=0 x(0)=x0=0 ,得:
{ s X ( s ) = A X ( s ) + B U ( s ) Y ( s ) = C X ( s ) + D U ( s ) \begin{cases} sX(s)=AX(s)+BU(s)\\[2ex] Y(s)=CX(s)+DU(s) \end{cases} ⎩⎨⎧sX(s)=AX(s)+BU(s)Y(s)=CX(s)+DU(s)
整理上式得:
Y ( s ) = [ C ( s I − A ) − 1 B + D ] U ( s ) Y(s)=[C(sI-A)^{-1}B+D]U(s) Y(s)=[C(sI−A)−1B+D]U(s)
定义传递函数矩阵:
W ( s ) = Y ( s ) U ( s ) = C ( s I − A ) − 1 B + D = ( W 11 W 12 ⋯ W 1 r W 21 W 22 ⋯ W 2 r ⋮ ⋮ ⋱ ⋮ W m 1 W m 2 ⋯ W m r ) W(s)=\frac{Y(s)}{U(s)}=C(sI-A)^{-1}B+D =\begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1r} \\ W_{21} & W_{22} & \cdots & W_{2r} \\ \vdots & \vdots & \ddots & \vdots \\ W_{m1} & W_{m2} & \cdots & W_{mr} \\ \end{pmatrix} W(s)=U(s)Y(s)=C(sI−A)−1B+D=⎝⎜⎜⎜⎛W11W21⋮Wm1W12W22⋮Wm2⋯⋯⋱⋯W1rW2r⋮Wmr⎠⎟⎟⎟⎞
说明:
- d i m ( W ( s ) ) = m × r , 其 中 d i m ( ⋅ ) 表 示 的 ⋅ 维 数 dim(W(s))=m\times r,其中 dim(\cdot) 表示的 \cdot 维数\\[2ex] dim(W(s))=m×r,其中dim(⋅)表示的⋅维数
- W i j = Y i ( s ) U j ( s ) , 它 表 征 第 j 个 输 入 对 第 i 个 输 出 的 传 递 关 系 。 W_{ij}=\frac{Y_i(s)}{U_j(s)},它表征第 j 个输入对第 i 个输出的传递关系。\\[2ex] Wij=Uj(s)Yi(s),它表征第j个输入对第i个输出的传递关系。
- 同 一 系 统 , 不 同 的 状 态 空 间 表 达 式 对 应 的 W ( s ) 是 相 同 的 。 同一系统,不同的状态空间表达式对应的W(s)是相同的。 同一系统,不同的状态空间表达式对应的W(s)是相同的。
1.6 状态矢量的线性变换
1.6.1 系统状态空间表达式的非唯一性
对于一个给定的定常系统,可以选取许多种状态变量,相应地有许多种状态空间表达式描述同一系统,也就是说系统可以有多种结构形式。所选取的状态矢量之间,实际上是一种矢量的线性变换(或称坐标变换)。
设 给 定 系 统 为 : { x ˊ = A x + B u , x ( 0 ) = x 0 y = C x + D u (11) 设给定系统为: \begin{cases} \acute{x}=Ax+Bu,x(0)=x_0\\[2ex] y=Cx+Du \end{cases}\tag{11} 设给定系统为:⎩⎨⎧xˊ=Ax+Bu,x(0)=x0y=Cx+Du(11)
可以找到任意一个非奇异矩阵 T T T ,将原状态矢量 x x x,作线性变换,得到另一状态矢量 z z z,设变换关系为:
x = T z , 即 : z = T − 1 x x=Tz,即:z=T^{-1}x x=Tz,即:z=T−1x
代入式(11),得到新的状态空间表达式:
{ z ˊ = T − 1 A T z + T − 1 B u , z ( 0 ) = T − 1 x ( 0 ) = T − 1 x 0 y = C T z + D u \begin{cases} \acute{z}=T^{-1}ATz+T^{-1}Bu,z(0)=T^{-1}x(0)=T^{-1}x_0\\[2ex] y=CTz+Du \end{cases} ⎩⎨⎧zˊ=T−1ATz+T−1Bu,z(0)=T−1x(0)=T−1x0y=CTz+Du
由于 T T T 为非奇异矩阵,故状态空间表达式为非唯一的。通常称 T T T 为变换矩阵。
1.6.2 系统特征值的不变性及系统的不变量
- 系统特征值
{ x ˊ = A x + B u y = C x + D u \begin{cases} \acute{x}=Ax+Bu\\[2ex] y=Cx+Du \end{cases} ⎩⎨⎧xˊ=Ax+Buy=Cx+Du
系统特征值就是系统矩阵 A A A 的特征值,也即特征方程:
∣ λ I − A ∣ = 0 (12) |\lambda I-A|=0 \tag{12} ∣λI−A∣=0(12)
的根。 - 系统的不变量与特征值的不变性
同一系统,经非奇异变换后,得:
{ z ˊ = T − 1 A T z + T − 1 B u , y = C T z + D u \begin{cases} \acute{z}=T^{-1}ATz+T^{-1}Bu,\\[2ex] y=CTz+Du \end{cases} ⎩⎨⎧zˊ=T−1ATz+T−1Bu,y=CTz+Du
其特征方程为:
∣ λ I − T − 1 A T ∣ = 0 (13) |\lambda I-T^{-1}AT|=0\tag{13} ∣λI−T−1AT∣=0(13)
式(12)与式(13)形式虽然不同,但实际是相等的,即系统的非奇异变换,其特征值是不变的。 - 特征矢量
对于系统矩阵 A A A ,若存在一非零向量 p p p ,使得 A p = λ p Ap=\lambda p Ap=λp,则称 p p p 为系统矩阵 A A A 对应于特征值 λ \lambda λ 的特征矢量。
1.6.3 状态空间表达式变换为约旦标准型
x ˊ = A x + B u , y = C x 变 换 为 : z ˊ = J z + T − 1 B u , y = C T x \acute{x}=Ax+Bu,y=Cx\\[2ex] 变换为:\acute{z}=Jz+T^{-1}Bu,y=CTx xˊ=Ax+Bu,y=Cx变换为:zˊ=Jz+T−1Bu,y=CTx
根据系统矩阵 A A A ,求其特征值,可以直接写出系统的约旦标准型矩阵 J J J :
参考文献
[1]:刘豹,唐万生. 现代控制理论[M]. 北京:机械工业出版社,2006.7
[2]:王孝武. 现代控制理论基础[M]. 3版 北京:机械工业出版社,2013.7
本次的分享就到这里
![]()
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “关注” “收藏” 一键三连哦!
更多精彩内容请前往 AXYZdong的博客
如果以上内容有任何错误或者不准确的地方,欢迎在下面 留个言。或者你有更好的想法,欢迎一起交流学习~~~