KMP-CF535D-Tavas and Malekas

KMP-CF535D-Tavas and Malekas

题意：

$$\begin{gathered} 给定模式串str，以及m个位置pos[i],1<=i<=m，要求从位置pos[i]开始的后缀子串的前缀要包含str， \\ 求满足条件的，长度为n的字符串共有多少种可能。 \end{gathered}$$

输入输出:

Input:
The first line contains two integers n and m, the length of s and the length of the subsequence Malekas wrote down (1 ≤ n ≤ 10⁶ and 0 ≤ m ≤ n - |p| + 1).

The second line contains string p (1 ≤ |p| ≤ n).

The next line contains m space separated integers y1, y2, …, ym, Malekas’ subsequence (1 ≤ y1 < y2 < … < ym ≤ n - |p| + 1).

Output:
In a single line print the answer modulo 1000 000 007.

Sample Input:
6 2
ioi
1 3

Sample Output:
26

Sample Input:
5 2
ioi
1 2

Sample Output:
0

Note:
In the first sample test all strings of form “ioioi?” where the question mark replaces arbitrary English letter satisfy.

Here |x| denotes the length of string x.

Please note that it’s possible that there is no such string (answer is 0).

EG:

$$\begin{gathered} 样例1：给定母串长度n=6，模式串长度m=3，模式串为ioi，要求从1,3位置开始的后缀子串的前缀为ioi， \\ 可以确定长度为6的母串的前5位字符为ioioi\_，第六位可填任意字母，因此满足题意的数量为26^1=26。 \end{gathered}$$

题解：

$$\begin{gathered} 一开始的想法是先计算相邻位置pos[i+1]与pos[i]之差，若差小于模式串长度len-1就无法满足条件， \\ 若恰好等于len-1，还需要判断模式串的第一个字符和最后一个字符是否相同，如样例2。 \end{gathered}$$

$现在发现了思考的漏洞:$

$如：模式串abab,长度len=4，若两个相邻位置间隔为1，1<4-1=3，却仍然可以满足题意。$

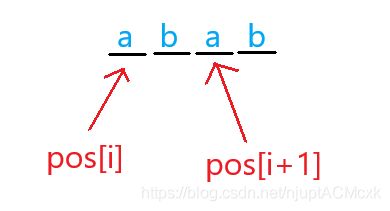
所以，判断的依据应当是模式串最长相同前后缀的长度！

$$\begin{gathered} 接下来需要统计相邻位置之间“可以填任意字母”的位置的个数，也不要忘了最后要判断总长度是否超过n。 \\ 求出总的“空位”个数cnt，再计算26^{cnt}即最终方案总数。 \end{gathered}$$

$用到最长相同前后缀的长度，想到KMP算法中的Next数组。$

$Next[i]：前i个字符中，前缀与后缀相同部分最长的长度。$

$所以我们对模式串求Next数组后，利用Next数组从模式串末尾开始，递归标记每一个循环节的前一个循环节的一端。$

$$\begin{gathered} 如：对模式串abab， \\ i：1234 \\ Next[i]:0012, \\ 我们把从末尾4开始标记，接着Next[4]=2，再把2标记。 \\ 若模式串长度减去相邻位置的间隔恰好被标记过， \\ 即len-(pos[i+1]-pos[i])在模式串中的位置恰好是前一个循环节的一端，说明可行。 \\ 反应到上图就是4-2=2，恰好是后一个循环节ab的前一个循环节ab的后端所在的位置。 \end{gathered}$$

具体落实：

$①、利用KMP中的Next数组来判断，从最后一个循环节向前标记每一个循环节的末端。$
$$\begin{gathered} ②、计算相邻位置的间隔，若间隔长度小于模式串的长度-1，则需要判断是否处在某循环节的末端位置。 \\ ③、计算所有“空位”的数量cnt，总的方案数即26^{cnt}。 \end{gathered}$$

注意:
$$\begin{gathered} ①、m=0的情况不能漏了特判。 \\ ②、最后一个位置的模式串可能会超过长度n。 \\ ③、第一个位置未必是1，因此第一个位置之前仍然可能存在“空位”。 \end{gathered}$$

---

代码:

#include
#include
#include
#include
#include
#define ll  long long
#define inf 0x7fffffff
using namespace std;
const int mod=1e9+7;
const int N=1e6+10;
int n,m,len;   ///len为模式串的长度
char s[N];
int pos[N],Next[N];
bool mark[N];   ///标记

void get_next()
{
     
    for(int i=2,j=0;i<=len;i++)
    {
     
        while(j&&s[i]!=s[j+1]) j=Next[j];
        if(s[i]==s[j+1]) j++;
        Next[i]=j;
    }
}

ll quick_pow(ll a,ll b)
{
     
    ll ans=1;
    while(b)
    {
     
        if(b&1) ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans%mod;
}

int main()
{
     
    cin>>n>>m;
    scanf("%s",s+1);
    if(!m) {
     printf("%lld\n",quick_pow(26,n));return 0;}   ///不能忘了特判m=0
    len=strlen(s+1);

    get_next();

    for(int i=len;i;i=Next[i]) mark[i]=true;

    for(int i=1;i<=m;i++)
    {
     
        scanf("%d",&pos[i]);
        if(i!=1&&pos[i]-pos[i-1]<len)   ///相邻位置间隔小于模式串长度的情况，需要判断是否被Next数组标记过
        {
     
            if(!mark[ pos[i-1]+len-pos[i] ])
            {
     
                cout<<0<<endl;
                return 0;
            }
        }
    }

    if(n-pos[m]<len-1) cout<<0<<endl;  ///判断最后一个位置是否会超过长度n
    else  ///统计空位的数量
    {
     
        int cnt=pos[1]-1;  ///第一个位置前的数字也是任意的
        for(int i=2;i<=m;i++)
            if(pos[i]-pos[i-1]>len)
                cnt+=pos[i]-pos[i-1]-len;

        cnt+=n-pos[m]-len+1;  ///加上最后一个位置到末尾的空位

        printf("%lld\n",quick_pow(26,cnt));
    }

    return 0;
}