【计算方法数值分析】顺序消去法、列主元素消去法、雅克比迭代法、高斯—赛德尔迭代法解线性方程组matlab编程实现及对比
【计算方法数值分析】消去法、迭代法解线性方程组
顺序消去法、列主元素消去法、雅克比迭代法、高斯—赛德尔迭代法

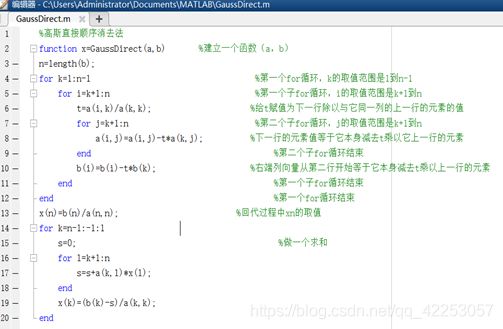
1.1、顺序消去法
a =
1.1348 3.8326 1.1651 3.4017
0.5301 1.7875 2.5330 1.5435
3.4129 4.9317 8.7643 1.3142
1.2371 4.9998 10.6721 0.0147
b =
9.5342
6.3941
18.4231
16.9237
x =
1.0000 1.0000 1.0000 1.0000
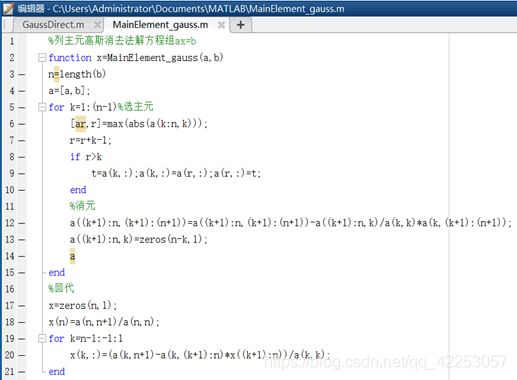
%列主元高斯消去法解方程组ax=b
function x=MainElement_gauss(a,b)
n=length(b)
a=[a,b];
for k=1:(n-1)%选主元
[ar,r]=max(abs(a(k:n,k)));
r=r+k-1;
if r>k
t=a(k,:);a(k,:)=a(r,:);a(r,:)=t;
end
%消元
a((k+1):n,(k+1):(n+1))=a((k+1):n,(k+1):(n+1))-a((k+1):n,k)/a(k,k)*a(k,(k+1):(n+1));
a((k+1):n,k)=zeros(n-k,1);
a
end
%回代
x=zeros(n,1);
x(n)=a(n,n+1)/a(n,n);
for k=n-1:-1:1
x(k,:)=(a(k,n+1)-a(k,(k+1):n)*x((k+1):n))/a(k,k);
end
a =
3.4129 4.9317 8.7643 1.3142 18.4231
0 1.0215 1.1717 1.3394 3.5326
0 2.1928 -1.7491 2.9647 3.4085
0 3.2122 7.4952 -0.4617 10.2457
a =
3.4129 4.9317 8.7643 1.3142 18.4231
0 3.2122 7.4952 -0.4617 10.2457
0 0 -6.8657 3.2799 -3.5858
0 0 -1.2118 1.4862 0.2743
a =
3.4129 4.9317 8.7643 1.3142 18.4231
0 3.2122 7.4952 -0.4617 10.2457
0 0 -6.8657 3.2799 -3.5858
0 0 0 0.9073 0.9073
x =
1.0000
1.0000
1.0000
1.0000
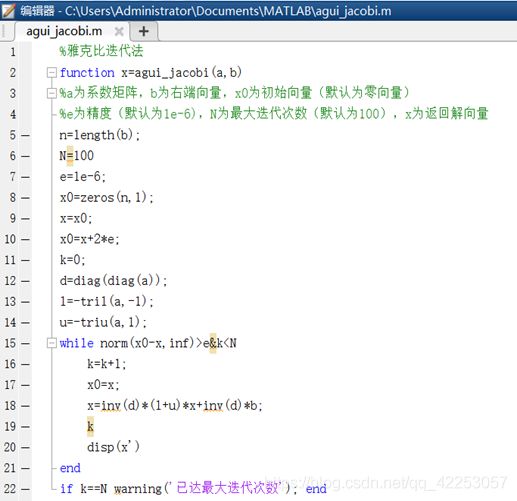
%雅克比迭代法
function x=agui_jacobi(a,b)
%a为系数矩阵,b为右端向量,x0为初始向量(默认为零向量)
%e为精度(默认为1e-6),N为最大迭代次数(默认为100),x为返回解向量
n=length(b);
N=100
e=1e-6;
x0=zeros(n,1);
x=x0;
x0=x+2*e;
k=0;
d=diag(diag(a));
l=-tril(a,-1);
u=-triu(a,1);
while norm(x0-x,inf)>e&k<N
k=k+1;
x0=x;
x=inv(d)*(l+u)*x+inv(d)*b;
k
disp(x')
end
if k==N warning('已达最大迭代次数'); end
k =
1
0 1.2500 -0.5000 1.2500 -0.5000 1.5000
k =
2
0.6250 1.0000 0.5000 1.0000 0.5000 1.2500
……………………
……………………
k =
39
1.0000 2.0000 1.0000 2.0000 1.0000 2.0000
x =
1.0000
2.0000
1.0000
2.0000
1.0000
2.0000
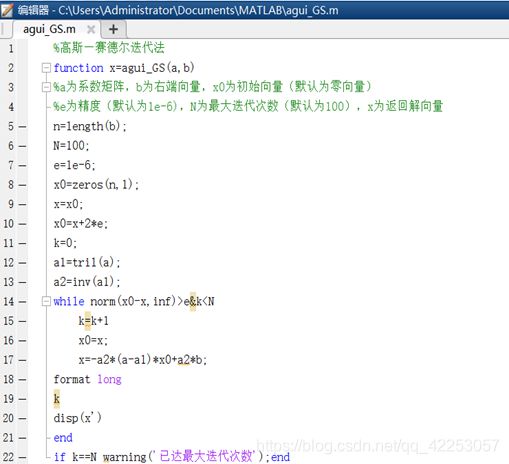
%高斯—赛德尔迭代法
function x=agui_GS(a,b)
%a为系数矩阵,b为右端向量,x0为初始向量(默认为零向量)
%e为精度(默认为1e-6),N为最大迭代次数(默认为100),x为返回解向量
n=length(b);
N=100;
e=1e-6;
x0=zeros(n,1);
x=x0;
x0=x+2*e;
k=0;
a1=tril(a);
a2=inv(a1);
while norm(x0-x,inf)>e&k<N
k=k+1
x0=x;
x=-a2*(a-a1)*x0+a2*b;
format long
k
disp(x')
end
if k==N warning('已达最大迭代次数');end
k =
1
1 至 5 列
0 1.250000000000000 -0.187500000000000 1.203125000000000 0.113281250000000
6 列
1.481445312500000
k =
2
1 至 5 列
0.613281250000000 1.384765625000000 0.517333984375000 1.560974121093750 0.606796264648438
6 列
1.781032562255859
…………………………
…………………………
k =
21
1 至 5 列
0.999999508971247 1.999999467301403 0.999999550421780 1.999999588778049 0.999999661534511
6 列
1.999999802989073
x =
0.999999508971247
1.999999467301403
0.999999550421780
1.999999588778049
0.999999661534511
1.999999802989073
- 直接顺序消去法相对于列主元消去法简单便捷无法排除大数吃小数产生的误差,在顺序消去法的过程中,如果出现akk=0,则消元无法进行,如果其绝对值值很小,把它作为除数,就会导致其他元素量级巨大增大和舍入误差的扩大,最后使计算结果失真
- 列主元消去法选主元的范围小,不改变未知数的次序,消元法稳定
- 雅克比迭代法与高斯—赛德尔迭代法都是随着迭代次数增多,解越来越接近于精确解雅克比迭代法的特点是公式简单,在每一步迭代过程中,用x(k)的全部分量代入求出x(k+1)的全部分量,为同步迭代法,但在雅克比的带过程中,对已经计算的信息未能充分利用,因此使用高斯—赛德尔迭代法每计算出一个新的分量便立即用它取代对应的旧的分量进行迭代,收敛速度更快。
- 从实验数据可以看出,同一个线性方程组用高斯—赛德尔迭代法迭代次数是K=21,而雅克比迭代法的迭代次数K=39,相较而言,高斯—赛德尔迭代法手链速度更快。