秒懂粒子群算法—— 附matlab源代码
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、什么是粒子群算法
- 二、程序代码
- 总结
前言
提示:以下是本篇文章正文内容,下面案例可供参考
一、粒子群算法简介
粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法,自然界中各种生物体均具有一定的群体行为,而人工生命的主要研究领域之一是探索自然界生物的群体行为,从而在计算机上构建其群体模型。
。
二、使用步骤
1.引入库
代码如下(示例):
%% 粒子群算法
clear
vars=1; %求解的维度
c1=1; c2=1; %粒子群步长参数
IS_limit=[8;-10]; %求解区域限制,第一个为最大值
k=0.5; w=0.5;
v_limit=[1;-1]; %粒子变化改变速度的限制,第二个为最小值
global m gen %定义粒子群的个数,粒子进化的代数
m=100; gen=50;
fun=@(x) x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式
funm=@(x) -(x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x)); %定义求解最小的值
%% 初始位置IS,变化速度v,位置最好记忆pa,全局最好位置pa_best
%根据设定的求解的范围进行均匀分布
rate=IS_limit(1,:)-IS_limit(2,:);
L=repmat(rate,m,1); %对最大与最小值间距进行重复
R=repmat(IS_limit(2,:),m,1); %对每个位置的最小量进行重复
IS=R+rand(m,vars).*L; %进行随机值的分配
pa=IS; %位置初始矩阵
result=funm(pa); %求解
[~,index]=min(result);
pa_best=pa(index,:); %初始化最优的初始位置
v=zeros(m,vars); %初始的速度全部设置为0
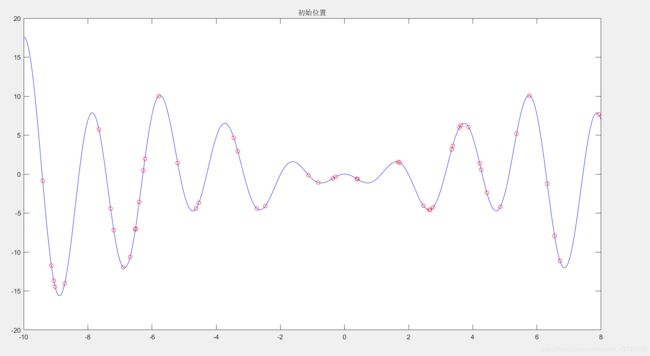
figure(3);
x0 =-10:0.01:8;
plot(x0,fun(x0),'b-',pa,fun(pa), 'ro');title('初始位置');
%% 粒子群开始迭代寻优,更行阶段
gen_now=1; %粒子群当前的代数
while gen_now<=gen
PA_best=repmat(pa_best,m,1);
v=w*v+c1*rand(m,vars).*(pa-IS)+c2*rand(m,vars).*(PA_best-IS); %速度更新矩阵
for i=1:vars %对于不满足要求的速度和可行解进行改变
for j=1:m
if v(j,i)
elseif v(j,i)>v_limit(1,i) %速度超过下限时
v(j,i)=v_limit(1,i);
end
end
end
IS=IS+v; %新的位置
for i=1:vars %对于不满足要求的速度和可行解进行改变
for j=1:m
if IS(j,i)
elseif IS(j,i)>IS_limit(1,i)
IS(j,i)=IS_limit(1,i) ; %位置超过下限时
end
end
end
fun_1=funm(IS); %此时每个位置对应函数值
fun_2=funm(pa); %之前每个位置对应函数值
logical=fun_1
result=funm(pa); %求解
[~,index]=min(result);
pa_best=pa(index,:); %初始化最优的初始位置
figure(2);
x0 =-10:0.01:8;
plot(x0,fun(x0), 'b-',IS,fun(IS),'ro');title('状态位置变化'); %所有粒子当前
pause(0.1)
gen_now=gen_now+1;
end
figure(1);
fplot(fun,[-10,8]);
hold on
plot(pa_best,fun(pa_best),'ro'); title('最终的目标值位置');
fun_max=fun(pa_best);
disp(['最大的值是=',num2str(fun_max)]);
disp(['位置在=',num2str(pa_best)]);
2.读入数据
代码如下(示例):
该处使用的url网络请求的数据。