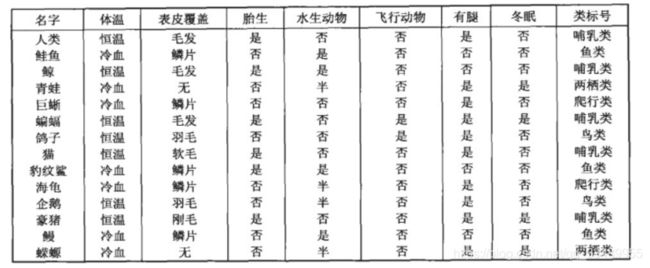
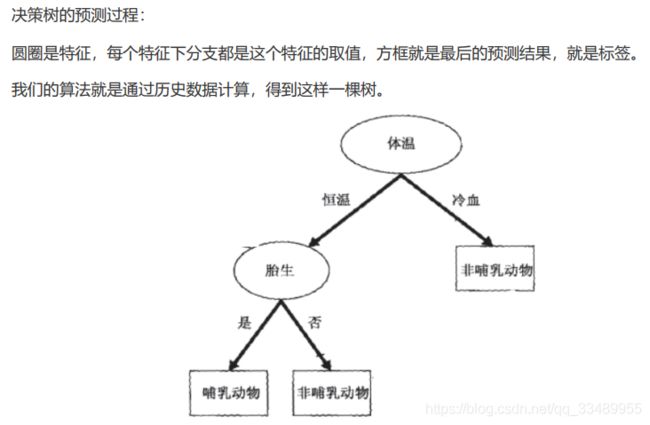
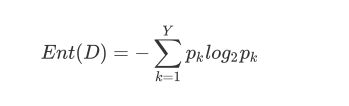机器学习 day3 决策树算法
决策树算法
- 1. 目的
- 2. 优缺点
- 3. 信息熵 entropy
-
- 计算方法:
-
- 导库:
- 导数据集:
- 首先计算原本的信息熵:
- 计算色泽特征下的信息熵:
-
- 取数据集D1 D1为色泽=青绿的数据子集
- 取子集D2 D2 为色泽=乌黑的数据子集
- 取子集D3 D3为色泽=浅白的数据子集
- 计算色泽特征的信息熵:
- 封装计算特征信息熵的函数:
- 结果:选择纹理作为根节点(信息熵小,信息增益就大)
- 4. sklearn 中的决策树
1. 目的
2. 优缺点
优点
- 易于理解:即使对于非分析背景的人来说,决策树输出也很容易理解。它不需要任何统计知识来阅
读和解释它们。它的图形表示非常直观。 - 在数据探索中很有用:决策树是识别最重要变量和两个或多个变量之间关系的最快方法之一。在决
策树的帮助下,我们可以创建具有更好预测目标变量能力的新变量(特征)。你可以参考一篇文章
(Trick to enhance power of regression model)。它也可以用于数据探索阶段。例如,我们正
在研究一个问题,即我们有数百个变量可用的信息,决策树将有助于识别最重要的变量。 - 需要更少的数据清理:与其他一些建模技术相比,它需要更少的数据清理。它不受异常值和缺失值
的影响。 - 数据类型不是约束:它可以处理数字和分类变量。
- 非参数方法:决策树被认为是非参数方法。这意味着决策树没有关于空间分布和分类器结构的假
设。
缺点
6. 过拟合:过拟合是决策树模型最实用的难点之一。 通过设置模型参数和修剪的约束来解决这个问
题。
7. 不适合连续变量:在处理连续数值变量时,决策树在对不同类别的变量进行分类时会丢失信息。
3. 信息熵 entropy
计算方法:
导库:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
导数据集:
watermelon = pd.read_excel('决策树-西瓜.xlsx')
watermelon
首先计算原本的信息熵:
resulte_ = watermelon['好瓜'].value_counts(normalize=True)
resulte_
否 0.529412
是 0.470588
Name: 好瓜, dtype: float64
Entropy = -(resulte_[0]*np.log2(resulte_[0])+resulte_[1]*np.log2(resulte_[1]))
Entropy
0.9975025463691153
计算色泽特征下的信息熵:
取数据集D1 D1为色泽=青绿的数据子集
D1 = watermelon[watermelon['色泽']=='青绿']
resulte_D1 = D1['好瓜'].value_counts(normalize=True)
#resulte_D1 查看色泽为青绿的好瓜坏瓜的占比
Entropy_D1 = -np.sum(resulte_D1*np.log2(resulte_D1))
#计算色泽=青绿的子集的信息熵
取子集D2 D2 为色泽=乌黑的数据子集
D2 = watermelon[watermelon['色泽']=='乌黑']
# D2 为色泽=乌黑的子集
resulte_D2 = D2['好瓜'].value_counts(normalize=True)
#resulte_D2 查看色泽为乌黑的好瓜坏瓜的占比
Entropy_D2 = -np.sum(resulte_D2*np.log2(resulte_D2))
#resulte_D2 查看色泽为乌黑的好瓜坏瓜的占比
取子集D3 D3为色泽=浅白的数据子集
D3 = watermelon[watermelon['色泽']=='浅白']
resulte_D3 = D3['好瓜'].value_counts(normalize=True)
Entropy_D3 = -np.sum(resulte_D3*np.log2(resulte_D3))
结果:
Entropy_D1,Entropy_D2,Entropy_D3 # (1.0, 0.9182958340544896, 0.7219280948873623)
(1.0, 0.9182958340544896, 0.7219280948873623)
计算色泽特征的信息熵:
Entropy_color = resulte_color[0]*Entropy_D1+Entropy_D2*resulte_color[1]+Entropy_D3*resulte_color[2]
Entropy_color # 0.88937738110375
0.88937738110375
封装计算特征信息熵的函数:
# data原始数据文本
# column特征名
#label 标签名
def entropy(data,column,label):
result_all = data[column].value_counts(normalize = True)
En_ = []
#result_all 为样本子集的占比
for feature in result_all.index:
#feature 为特征column的取值
sub_datasezts = data[data[column]==feature]
#取出特征column = feature子集(色泽=青绿)
resulte_sub = sub_datasezts[label].value_counts(normalize = True)
#特征子集中标签的pi
entropy_sub = -np.sum(resulte_sub*np.log2(resulte_sub))
#特征子集的entropy
En_.append(entropy_sub)
# 存储子集的entropy
entropy = np.sum(result_all*np.array(En_))
#计算特征column的entropy
return entropy
计算:
features = watermelon.columns[1:-1]
features # Index(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'], dtype='object')
columns = watermelon.columns[1:-1]
entropy_ = []
for features in columns:
entropy_.append(entropy(watermelon,features,'好瓜'))
[*zip(columns,entropy_)]
"""
[('色泽', 0.88937738110375),
('根蒂', 0.8548275868023224),
('敲声', 0.8567211127541194),
('纹理', 0.6169106490008467),
('脐部', 0.7083437635274363),
('触感', 0.9914560571925497)]
"""
结果:选择纹理作为根节点(信息熵小,信息增益就大)
4. sklearn 中的决策树
from sklearn.tree import DecisionTreeClassifier
DT = DecisionTreeClassifier(
criterion='gini',
max_depth=None, # 限制树的最大深度
min_samples_split=2,
min_samples_leaf=1,
max_features=None,# 限制最大的特征个数
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
)
将特征转化为数字编码:
处理字符串通常有以下几种方式:
- 有序变量(Ordinal Variable):字符串表示的数据有大小关系,那么可以对字符串进行序号化处理。
- 分类变量(Categorical Variable)/ 名义变量(Nominal Variable):字符串表示的数据没有大小关系和等级之分,那么就可以使用独热编码处理成哑变量(虚拟变量)矩阵。
- 定距变量(Scale Variable):数据有大小高低之分,可以进行加减运算。
watermelon['触感']=1*(watermelon['触感']=='硬滑')
独热编码:
from sklearn.preprocessing import OneHotEncoder
OH = OneHotEncoder().fit(watermelon[['色泽', '根蒂', '敲声', '纹理', '脐部']])
X = OH.transform(watermelon[['色泽', '根蒂', '敲声', '纹理', '脐部']]).toarray()
OH.categories_
"""
[array(['乌黑', '浅白', '青绿'], dtype=object),
array(['硬挺', '稍蜷', '蜷缩'], dtype=object),
array(['沉闷', '浊响', '清脆'], dtype=object),
array(['模糊', '清晰', '稍糊'], dtype=object),
array(['凹陷', '平坦', '稍凹'], dtype=object)]
"""
将处理好的编码转成 dataframe
X = pd.DataFrame(X,columns=OH.get_feature_names())
X['触感']=watermelon['触感']
X.head()
| x0_乌黑 | x0_浅白 | x0_青绿 | x1_硬挺 | x1_稍蜷 | x1_蜷缩 | x2_沉闷 | x2_浊响 | x2_清脆 | x3_模糊 | x3_清晰 | x3_稍糊 | x4_凹陷 | x4_平坦 | x4_稍凹 | 触感 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1 |
| 1 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1 |
| 2 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1 |
| 3 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1 |
| 4 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1 |
测试并修改参数:
y = watermelon['好瓜']
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(X,y)
训练集 1 测试集 0.6
score = []
score_train = []
for i in np.arange(1,20):
DT = DecisionTreeClassifier(min_samples_leaf=i).fit(xtrain,ytrain)
score_train.append(DT.score(xtrain,ytrain))
score.append(DT.score(xtest,ytest))
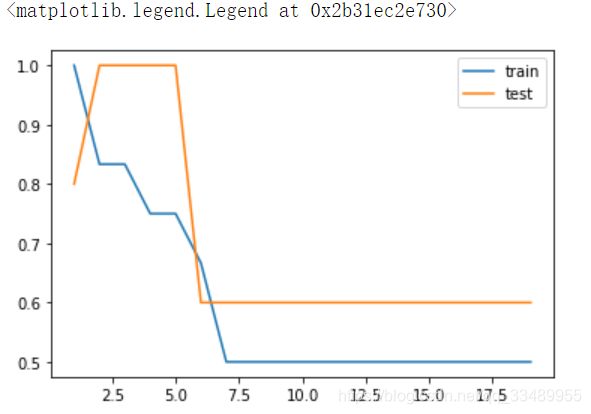
plt.plot(np.arange(1,20),score_train,label = 'train')
plt.plot(np.arange(1,20),score,label = 'test')
plt.legend()
from sklearn.preprocessing import OrdinalEncoder
OE = OrdinalEncoder().fit(df[['色泽', '根蒂', '敲声', '纹理', '脐部']])
OE.transform(df[['色泽', '根蒂', '敲声', '纹理', '脐部']])
OE.categories_