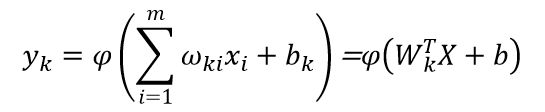人工神经网络—感知器算法
感知器算法
- 1. 回顾
- 2. 感知器算法
-
- 2.1 感知器算法的实现步骤
- 2.2 算法能停得下来吗?
- 2.3 基于增广向量的感知器算法
- 2.4 感知器算法收敛定理
- 3. 感知器算法收敛的MATLAB程序演示
- 参考资料
在这一讲中,我们将重点介绍美国科学家Frank Rosenblatt(1928-1971)如何对神经元的MP模型进行改造,用于解决二分类的问题。

1. 回顾
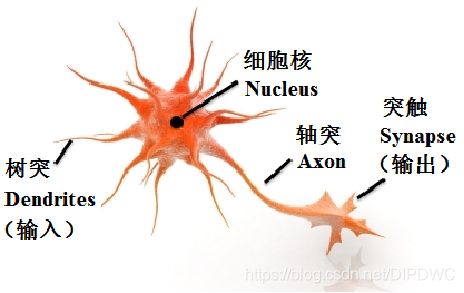
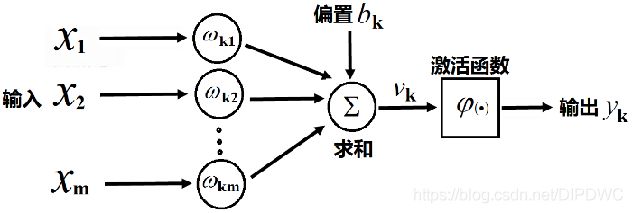
回顾上一讲的内容,神经元的MP模型:
2. 感知器算法
1957年,Frank Rosenblatt从纯数学的度重新考察这一模型,指出能够从一些输入输出对(X,y)中通过机器学习算法自动获得权重W和偏置b,以此,他提出感知器算法(Perceptron Algorithm)。
2.1 感知器算法的实现步骤
这里我们仍然假设输入的样本表示为给定一些输入输出对( X i X_i Xi, y i y_i yi), i i i=1~N,这是一个二分类问题,其中, X i X_i Xi是训练数据; y i = ± 1 y_i=±1 yi=±1,分别代表相应的类别。
我们的任务是要找一个向量W和一个常数b,使得对 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,有
(1) y i = + 1 y_i=+1 yi=+1,则 W T X i + b > 0 W^TX_i+b>0 WTXi+b>0
(2) y i = − 1 y_i=-1 yi=−1,则 W T X i + b < 0 W^TX_i+b<0 WTXi+b<0
把某个训练数据 X i X_i Xi满足上述的条件,叫作这个数据获得了平衡,否则没有获得平衡。可见,一个数据 X i X_i Xi没有获得平衡也有两种情况:
(1) y i = + 1 y_i=+1 yi=+1,则 W T X i + b < 0 W^TX_i+b<0 WTXi+b<0
(2) y i = − 1 y_i=-1 yi=−1,则 W T X i + b > 0 W^TX_i+b>0 WTXi+b>0
可以看到,这个任务与前面支持向量机的任务完全一致。
我们已经学习过,当且仅当在训练数据集线性可分的情况下,才能找到W和b满足使所有的 n n n个训练样本都达到平衡,感知器算法给出了另一种不同于支持向量机寻找W和b的方法,其做法包含如下四个步骤:
(1)随机选择W和b。
(2)取一个训练样本(X,y)
(i) 若 W T X + b > 0 W^TX+b>0 WTX+b>0且 y = − 1 y=-1 y=−1,则:
w = W − X , b = b − 1 w=W-X,b=b-1 w=W−X,b=b−1
(ii) 若 W T X + b < 0 W^TX+b<0 WTX+b<0且 y = + 1 y=+1 y=+1,则:
w = W + X , b = b + 1 w=W+X,b=b+1 w=W+X,b=b+1
(3)再取另一个(X,y) ,回到(2)
(4)终止条件:直到所有输入输出对都不满足(2)中(i)和(ii)之一,退出循环
从第二步(2)可以看出,这是一个没有达到平衡状态的情况,因此,我们需要对W和b进行调整。
分析第二步(2)的第一种情形,即当 y = − 1 y=-1 y=−1时,调整方式如下:
W ( 新 ) = W ( 旧 ) − X , b ( 新 ) = b ( 旧 ) − 1 W(新)=W(旧)-X,b(新)=b(旧)-1 W(新)=W(旧)−X,b(新)=b(旧)−1
将上式代入下式
W ( 新 ) T X + b ( 新 ) = ( W ( 旧 ) − X ) T X + b ( 旧 ) − 1 = [ W ( 旧 ) T X + b ( 旧 ) ] − ( X T X + 1 ) = [ W ( 旧 ) T X + b ( 旧 ) ] − ( ∣ ∣ X ∣ ∣ 2 + 1 ) ≤ [ W ( 旧 ) T X + b ( 旧 ) ] − 1 W(新)^TX+b(新)=(W(旧)-X)^TX+b(旧)-1= [W(旧)^TX+b(旧)]-(X^TX+1)= [W(旧)^TX+b(旧)]-(||X||^2+1)≤[W(旧)^TX+b(旧)]-1 W(新)TX+b(新)=(W(旧)−X)TX+b(旧)−1=[W(旧)TX+b(旧)]−(XTX+1)=[W(旧)TX+b(旧)]−(∣∣X∣∣2+1)≤[W(旧)TX+b(旧)]−1
使得 X X X距离平衡状态至少近了一点;
当 y = + 1 y=+1 y=+1时,
W ( 新 ) = W ( 旧 ) + X , b ( 新 ) = b ( 旧 ) + 1 W(新)=W(旧)+X,b(新)=b(旧)+1 W(新)=W(旧)+X,b(新)=b(旧)+1
将上式代入下式
W ( 新 ) T X + b ( 新 ) = ( W ( 旧 ) + X ) T X + b ( 旧 ) + 1 = [ W ( 旧 ) T X + b ( 旧 ) ] + ( X T X + 1 ) = [ W ( 旧 ) T X + b ( 旧 ) ] + ( ∣ ∣ X ∣ ∣ 2 + 1 ) ≥ [ W ( 旧 ) T X + b ( 旧 ) ] + 1 W(新)^TX+b(新)=(W(旧)+X)^TX+b(旧)+1= [W(旧)^TX+b(旧)]+(X^TX+1)= [W(旧)^TX+b(旧)]+(||X||^2+1)≥[W(旧)^TX+b(旧)]+1 W(新)TX+b(新)=(W(旧)+X)TX+b(旧)+1=[W(旧)TX+b(旧)]+(XTX+1)=[W(旧)TX+b(旧)]+(∣∣X∣∣2+1)≥[W(旧)TX+b(旧)]+1
使得 W T X + b W^TX+b WTX+b的值比原来至少大了1。
2.2 算法能停得下来吗?
有没有可能出现W和b在某一步的变化使某个数据从不平衡状态达到了平衡状态,但同时却使另一个数据从平衡状态变为了不平衡状态呢?如果是这样,将有可能出现循环无法终止的局面。
Rosenblatt发明感知器算法时,最具创意的一步是严格地证明了只要训练数据线性可分,那么感知器算法一定可以停下来。
在描述这个定理的时候,我们需要做一些定义,对于某个训练数据 X i X_i Xi,我们定义它的增广向量如下:
(1)若 y i = + 1 y_i=+1 yi=+1,则 x ⃗ i = [ x i 1 ] \vec x_i=\left[ \begin{matrix} x_i\\ 1 \end{matrix} \right] xi=[xi1]
(2)若 y i = − 1 y_i=-1 yi=−1,则 x ⃗ i = [ − x i − 1 ] \vec x_i=\left[ \begin{matrix} -x_i\\ -1 \end{matrix} \right] xi=[−xi−1]
定义增广向量的目的是简化我们的表达,原任务是寻找 ( W , b ) (W,b) (W,b)使得 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,有:
(1) y i = + 1 y_i=+1 yi=+1,则 W T X i + b > 0 W^TX_i+b>0 WTXi+b>0
(2) y i = − 1 y_i=-1 yi=−1,则 W T X i + b < 0 W^TX_i+b<0 WTXi+b<0
有了增广向量这个定义后,简化表达为寻找 W = [ W b ] \ W=\left[ \begin{matrix} W\\ b \end{matrix} \right] W=[Wb]使得对 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,有:
W T x ⃗ i > 0 W^T\vec x_i>0 WTxi>0
2.3 基于增广向量的感知器算法

最初是随机的寻找一个W,接下来如果对于 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N的某一个 i i i,若 W T x ⃗ i ≤ 0 W^T\vec x_i≤0 WTxi≤0,那么 w = w + x ⃗ i w=w+\vec x_i w=w+xi,以此循环直到对于所有的 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N, W T x ⃗ i > 0 W^T\vec x_i>0 WTxi>0为止。
可以证明基于增广向量的感知器算法和原来的感知器算法也是完全等价的。
下面利用增广向量的感知器算法来证明感知器算法收敛定理。
2.4 感知器算法收敛定理
对于 N N N个增广向量 x ⃗ 1 , x ⃗ 2 , ⋅ ⋅ ⋅ , x ⃗ N \vec x_1,\vec x_2,···,\vec x_N x1,x2,⋅⋅⋅,xN,如果存在一个权重向量 w o p t w_{opt} wopt,使得对于每一个 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,有
w o p t T x ⃗ i > 0 w_{opt}^T\vec x_i>0 woptTxi>0
运用上述感知器算法,在有限步内找到一个 w w w,使得对所有的 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,有 w T x ⃗ i > 0 w^T\vec x_i>0 wTxi>0。
需要注意的是这个定理的一个条件,即存在一个权重向量 w o p t w_{opt} wopt使得对于每一个 x ⃗ i \vec x_i xi的增广向量有 w o p t t x ⃗ i > 0 w_{opt}^t\vec x_i>0 wopttxi>0,这个条件与训练数据集线性可分是完全等价的。另外需要注意,当训练数据集线性可分的情况下,最终在有限步内找到的 w w w不一定是 w o p t w_{opt} wopt,回顾线性可分的定义,如果存在一个超平面分开两类,则一定存在无数个平面分开两类,而 w w w与 w o p t w_{opt} wopt是这无数多个超平面中的两个。
感知器收敛定理证明如下:
首先我们假设 ∣ ∣ w o p t ∣ ∣ = 1 ||w_{opt}||=1 ∣∣wopt∣∣=1(向量 W ⃗ \vec W W和 a W ⃗ a\vec W aW代表的是同一个平面,因此我们可以用一个 a a a去加权 w o p t w_{opt} wopt,使 ∣ ∣ w o p t ∣ ∣ = 1 ||w_{opt}||=1 ∣∣wopt∣∣=1)
定义 w ( k ) w(k) w(k)为第 k k k次改变后的权重向量值,那么会有以下两种情况:
情况1:
如果 w ( k ) T x ⃗ i > 0 {w(k)}^T\vec x_i>0 w(k)Txi>0对所有 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N,那么所有点已经达到平衡,感知器算法收敛。
情况2:
如果存在某个 i i i,使得 w ( k ) T x ⃗ i ≤ 0 {w(k)}^T\vec x_i≤0 w(k)Txi≤0,那么根据感知器算法 w ( k + 1 ) = w ( k ) + x ⃗ i w(k+1)=w(k)+\vec x_i w(k+1)=w(k)+xi
将这个式子两边同时减去 a w o p t aw_{opt} awopt,得
w ( k + 1 ) − a w o p t = w ( k ) − a w o p t + x ⃗ i w(k+1)-aw_{opt}=w(k)-aw_{opt}+\vec x_i w(k+1)−awopt=w(k)−awopt+xi
注: a w o p t aw_{opt} awopt与 w o p t w_{opt} wopt代表的是同一个超平面。
取模并展开
∣ ∣ w ( k + 1 ) − a w o p t ∣ ∣ 2 = ∣ ∣ w ( k ) − a w o p t + x ⃗ i ∣ ∣ 2 = ∣ ∣ w ( k ) − a w o p t ∣ ∣ 2 + ∣ ∣ x ⃗ i ∣ ∣ 2 + 2 w ( k ) T x ⃗ i − 2 a w o p t T x ⃗ i ||w(k+1)-aw_{opt}||^2=||w(k)-aw_{opt}+\vec x_i||^2=||w(k)-aw_{opt}||^2+||\vec x_i||^2+2w(k)^T\vec x_i-2aw_{opt}^T\vec x_i ∣∣w(k+1)−awopt∣∣2=∣∣w(k)−awopt+xi∣∣2=∣∣w(k)−awopt∣∣2+∣∣xi∣∣2+2w(k)Txi−2awoptTxi
因为 w ( k ) T x ⃗ i ≤ 0 {w(k)}^T\vec x_i≤0 w(k)Txi≤0,因此有:
∣ ∣ w ( k + 1 ) − a w o p t ∣ ∣ 2 ≤ ∣ ∣ w ( k ) − a w o p t ∣ ∣ 2 + ∣ ∣ x ⃗ i ∣ ∣ 2 − 2 a w o p t T x ⃗ i ||w(k+1)-aw_{opt}||^2≤||w(k)-aw_{opt}||^2+||\vec x_i||^2-2aw_{opt}^T\vec x_i ∣∣w(k+1)−awopt∣∣2≤∣∣w(k)−awopt∣∣2+∣∣xi∣∣2−2awoptTxi
又由于:
对任意的 i = 1 ⋅ ⋅ ⋅ N i=1···N i=1⋅⋅⋅N, w o p t T > ⃗ 0 w_{opt}^T\vec >0 woptT>0,而 ∣ ∣ x ⃗ i ∣ ∣ 2 ||\vec x_i||^2 ∣∣xi∣∣2是一个有界的值,那么我们一定可以取一个足够大的 a a a,使得 ∣ ∣ x ⃗ i ∣ ∣ 2 − 2 a w o p t T x ⃗ i < − 1 ||\vec x_i||^2-2aw_{opt}^T\vec x_i<-1 ∣∣xi∣∣2−2awoptTxi<−1
我们有:
∣ ∣ w ( k + 1 ) − a w o p t ∣ ∣ 2 ≤ ∣ ∣ w ( k ) − a w o p t ∣ ∣ 2 − 1 ||w(k+1)-aw_{opt}||^2≤||w(k)-aw_{opt}||^2-1 ∣∣w(k+1)−awopt∣∣2≤∣∣w(k)−awopt∣∣2−1
w w w的值每更新一次,它离 a w o p t aw_{opt} awopt的距离至少减少1个单位。
假设: w w w的初值为 w ( 0 ) w(0) w(0),经过 ∣ ∣ w ( 0 ) − a w o p t ∣ ∣ 2 ||w(0)-aw_{opt}||^2 ∣∣w(0)−awopt∣∣2 次迭代, w w w一定会收敛到 a w o p t aw_{opt} awopt。当然,也有可能没有经过这么多次迭代,感知器算法已经收敛并退出循环了。
以上完成了感知器算法的证明。
3. 感知器算法收敛的MATLAB程序演示
下面这幅图是二维特征空间线性可分的例子
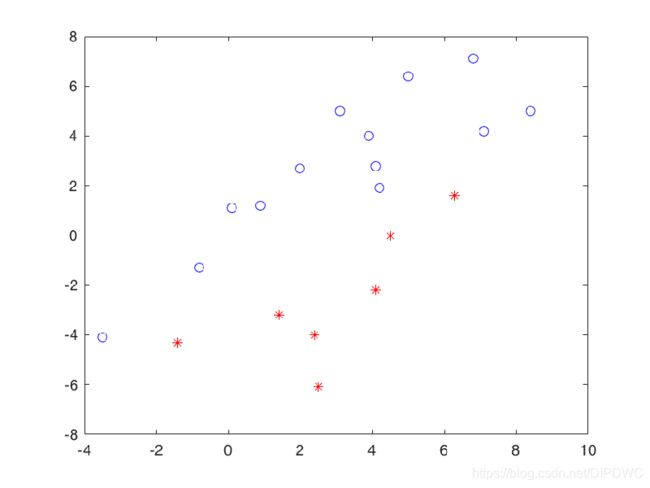
设置最初的 w w w值,如下图直线所示

接下来,调用感知器算法不断的更新这条直线的方程。
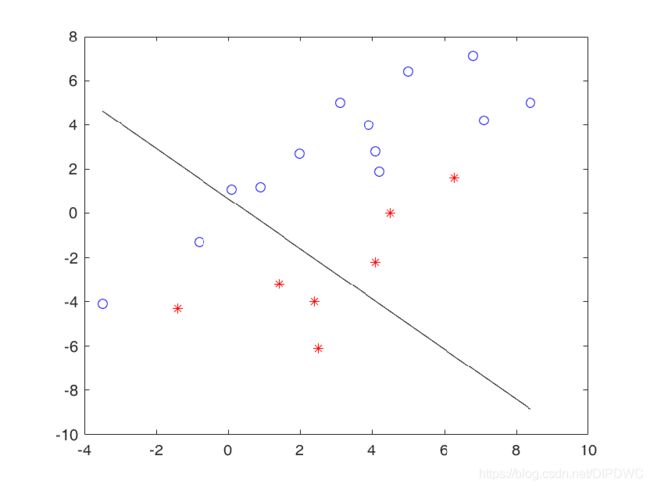



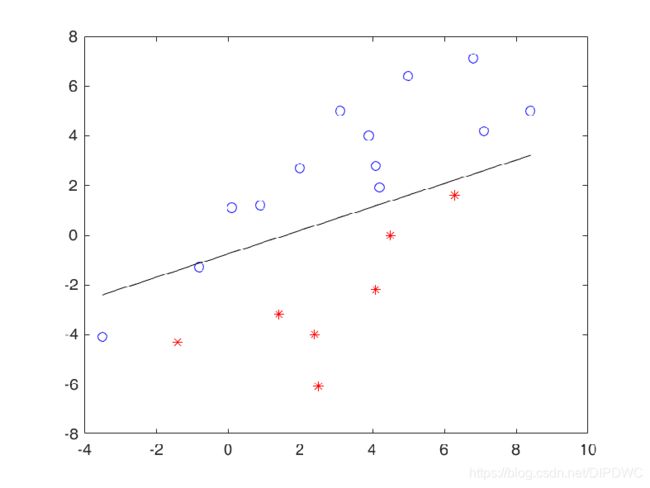
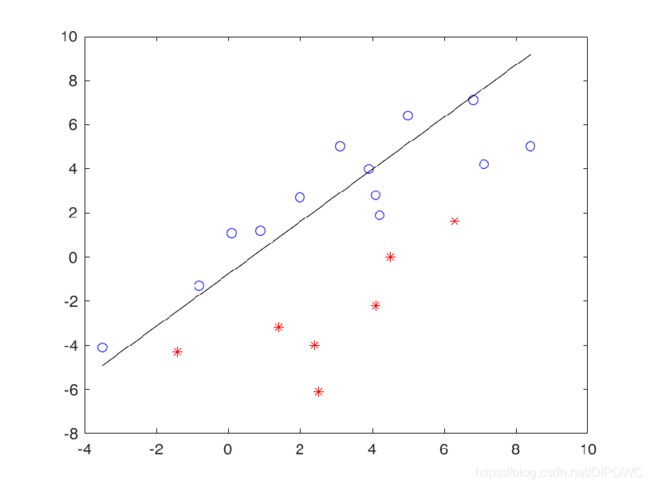



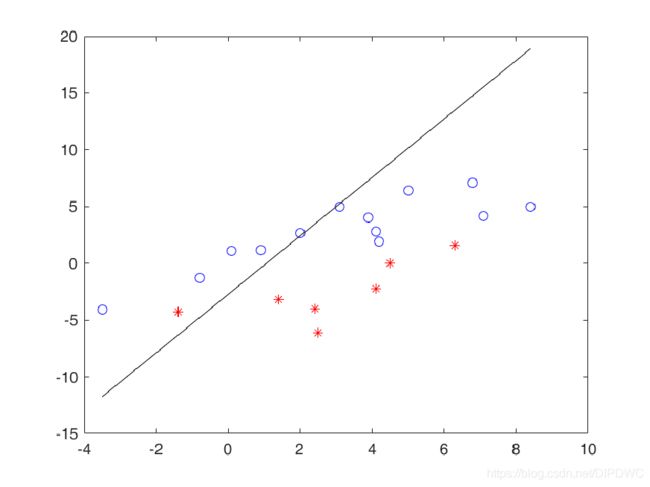
可以看到这条直线以一种无规律的方式不断运动,似乎看不到它收敛的时候,但是感知器算法收敛定理保证了只要训练数据集线性可分,就一定能收敛。
最后,经过多轮的迭代后,它收敛到了这里,完全分开了两个类别。

作为本讲的结束,有两道思考题:
(1)如果训练数据集线性不可分,那么感知器算法是否还收敛呢?请证明你的结论。
(2)如果此时感知器算法不收敛,你能否改造一下这个算法,使它在线性不可分的情况下,能自动终止循环呢?
参考资料
- 浙江大学《机器学习》课程—胡浩基老师主讲
如果文章对你有帮助,请记得点赞与关注,谢谢!
![]()