二叉树遍历的应用之分治法

而它属于五大常用算法之一，而五大常用算法为：分治、动态规划、贪心、回溯、分支界定。下面来看一下具体相关的算法。

查找技术：

首先是查找相关的算法，其中分为顺序查找和二分查找，下面分别来看一下。

顺序查找：

如果线性表为无序表，即表中元素的排列是无序的，则不管线性表采用顺序存储还是链式存储，都必须使用顺序查找。

如果线性表有序，但采用链式存储结构，则也必须使用顺序查找。

这个比较简单，举一个例子既可：

二分查找：

明提条件：数据已经排好序。

《编程珠玑》里说过：大约10%的专业程序员，才能够正确地写出二分查找。尽管第一个二分查找程序于1946年就公布了，但是第一个没有bug的程序在1962年才出现。

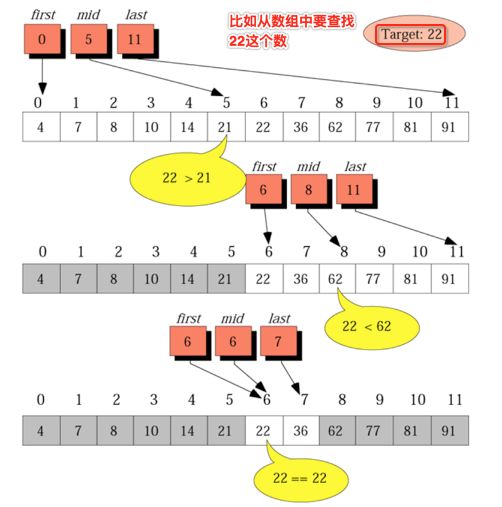
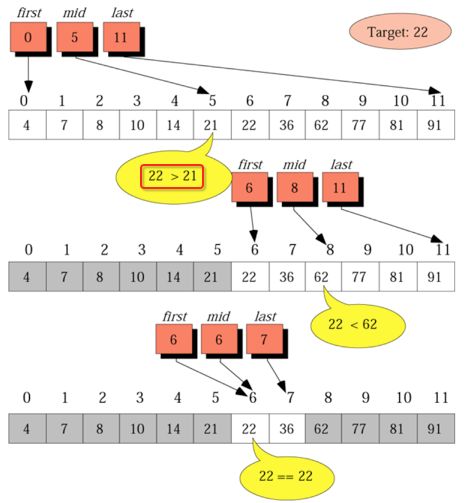
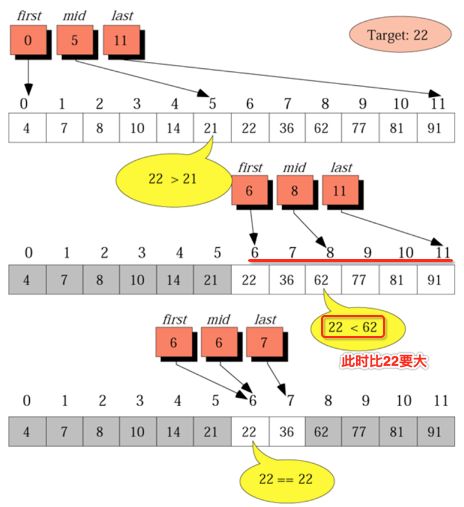
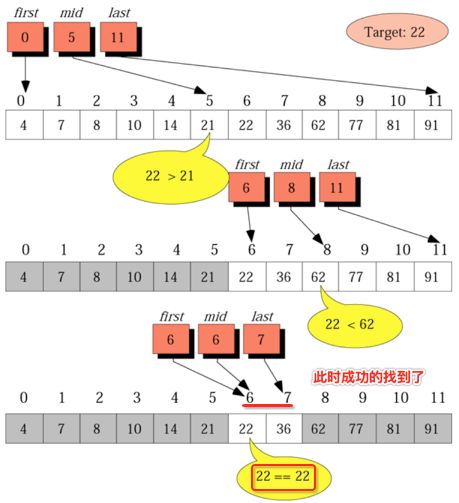
呃，有这么夸张么？二分查找不是一个比较常见的算法嘛，其实确实是有原因的，很容易犯错，下面先来看一下二分查找的一个思想：

此时折半一下，则算出中间位置为(0+11)/ 2 = 5，所以用这个位置的数跟我们要查找的22进行对比，很明显中间的数要小：

所以此时的搜索范围则变为5位置往右，因为前提该数列是从小到大顺序已经排好顺序了嘛，所以此时则搜索范围定位到6~11的位置了，以此进行折半再进行对比：

所以则应该从剩下范围中的左侧来进行搜寻，类似的逻辑进行折半查找：

可以看到每次都是折半进行搜索，它的时间复杂度为O(n) = log2(n)，比如对于1000个元素，其大概算9次就可以查找出来了，效果还是比较高的，接下来撸码来实现它，之前也说了这里二分法一般人都会写错，那下面来看一下怎么个容易出错：

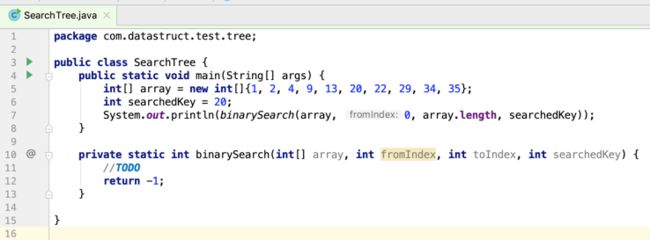
搭了一个架子，接下来则就是来实现二分查找的逻辑了，坑就会出现了，通常咱们可能会这样来写：

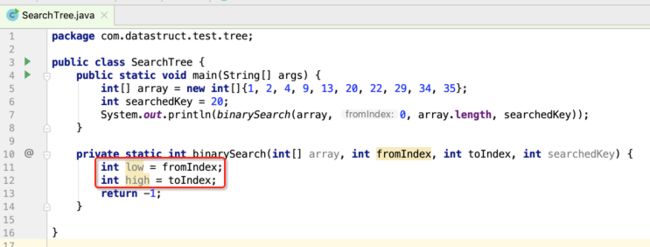
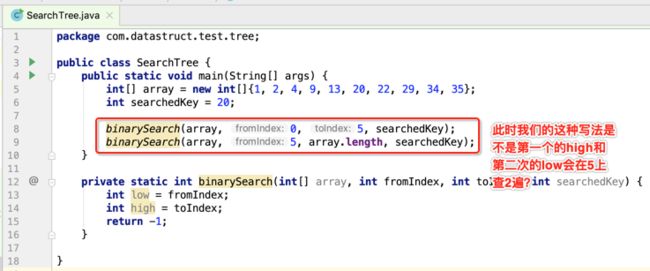
这里要强调的是大部分写二分查找出错的原因就出在这了，是关于一个数据范围连续的问题，应该用左闭右开的原则来写，如果像上面这样写，其low和high会重复了，比如：

所以注意了！！！！得这样写才是正确的：

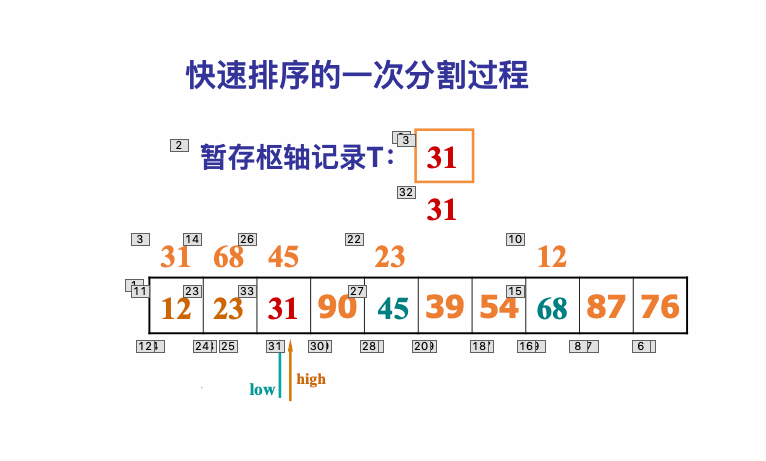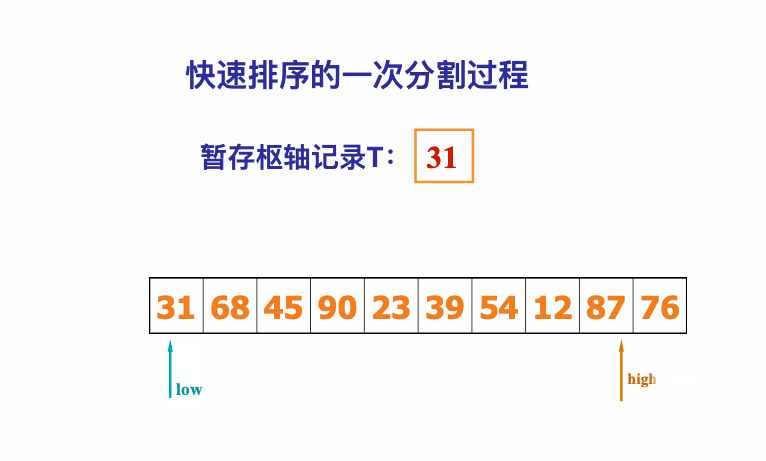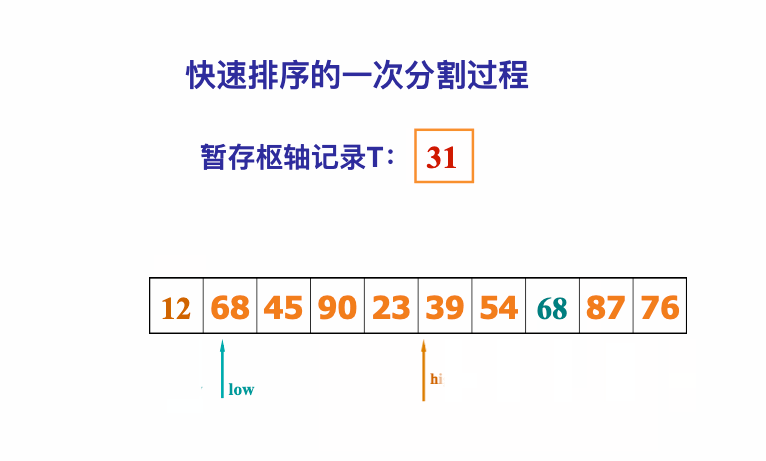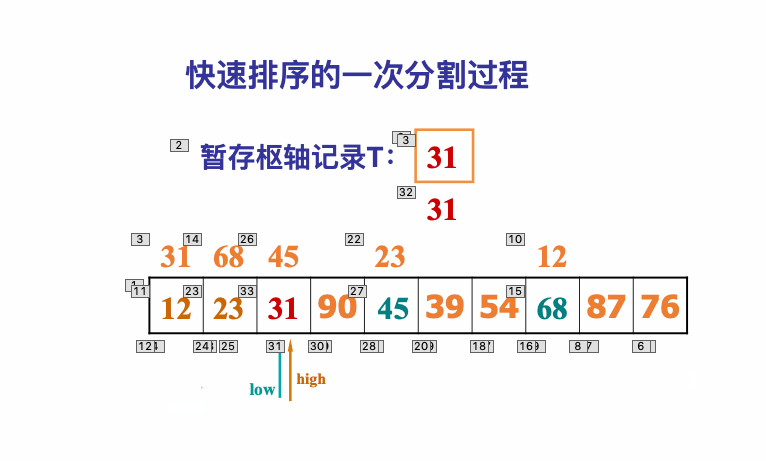
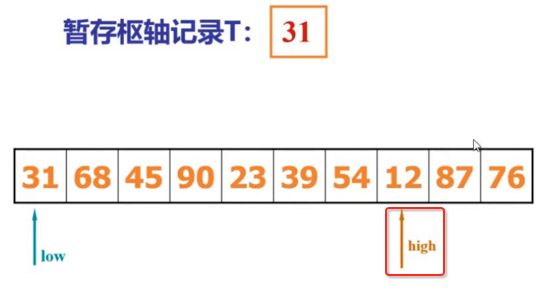
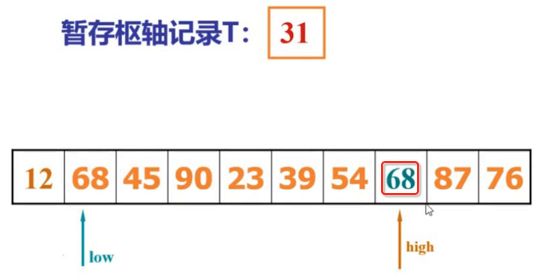
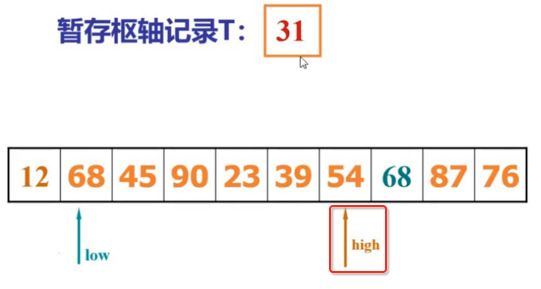
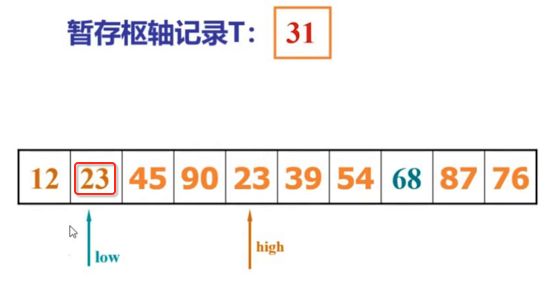
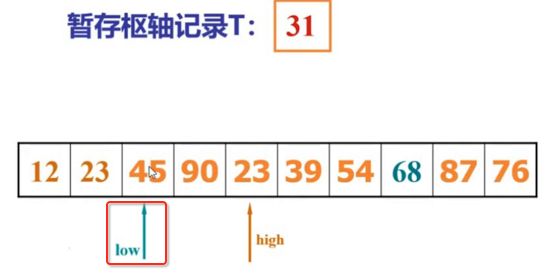
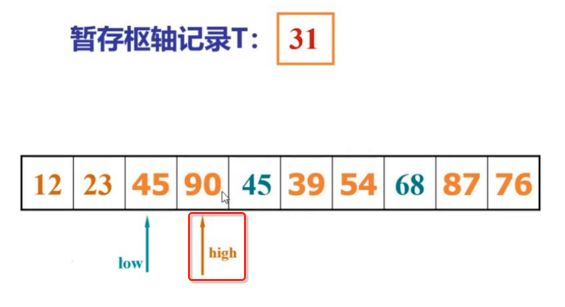
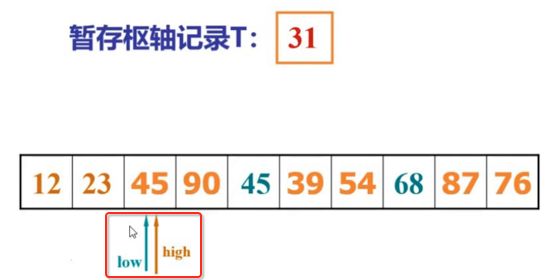
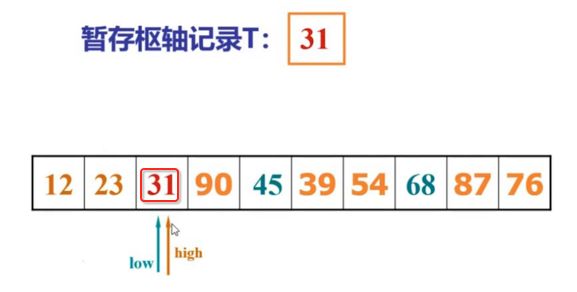
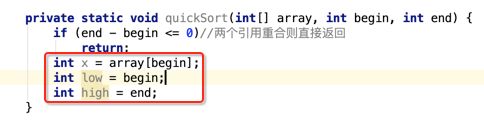
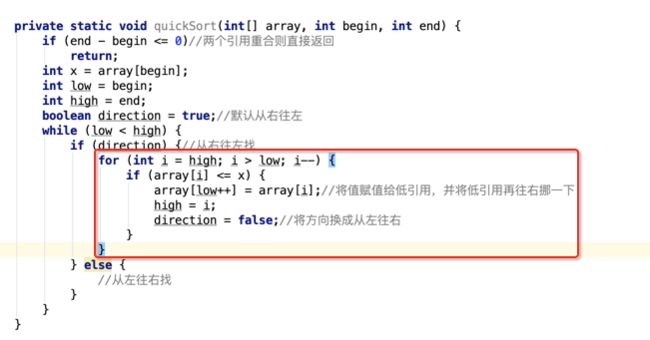
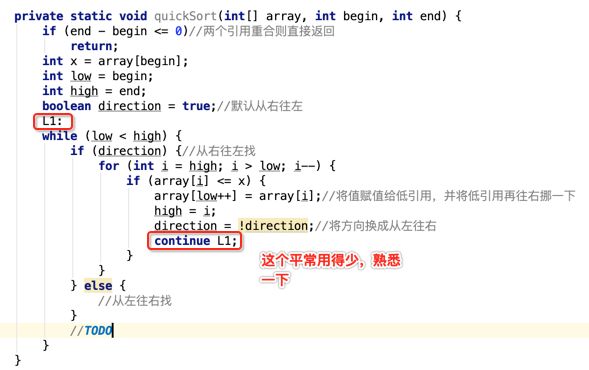
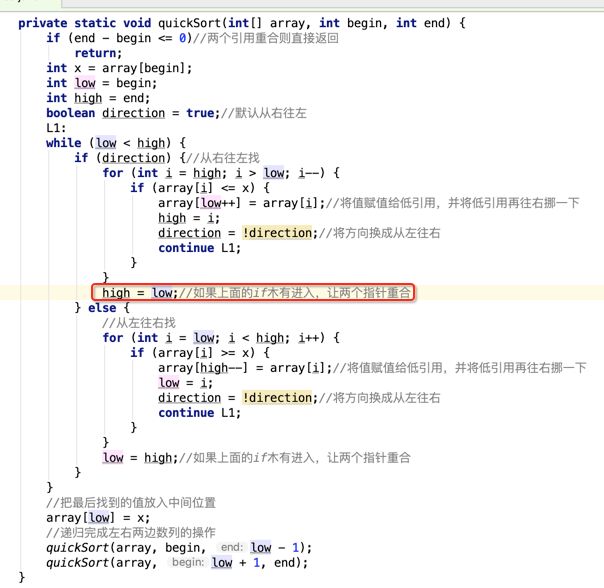
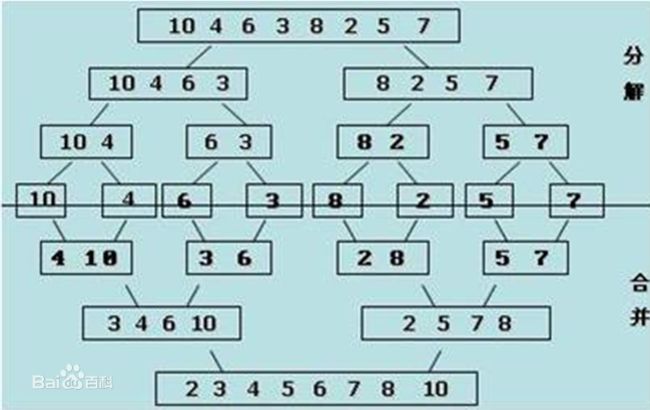
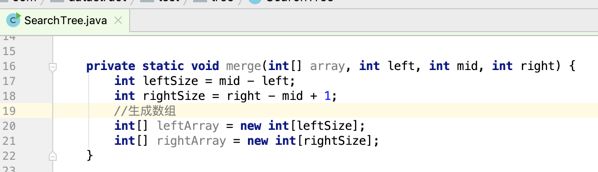
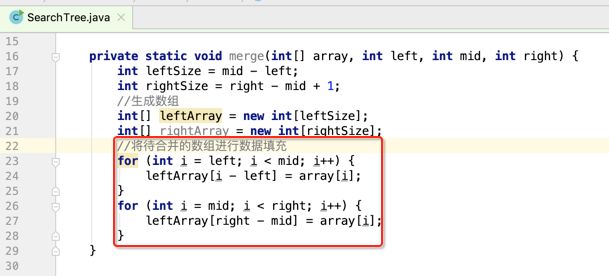
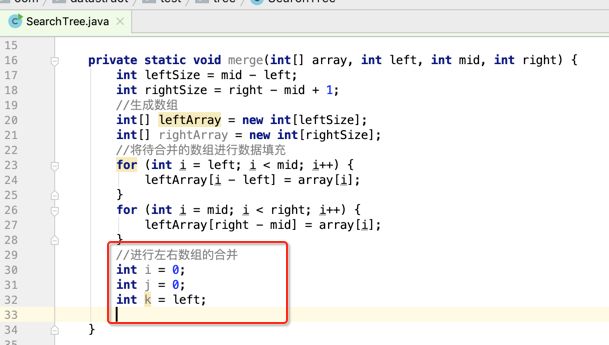
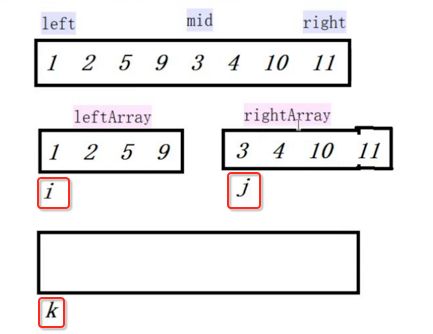
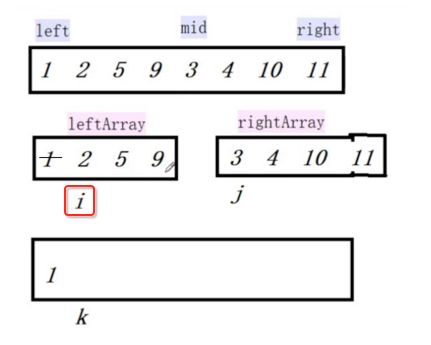
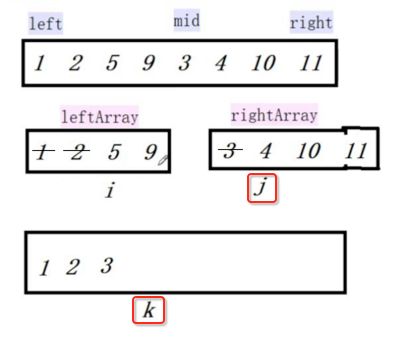
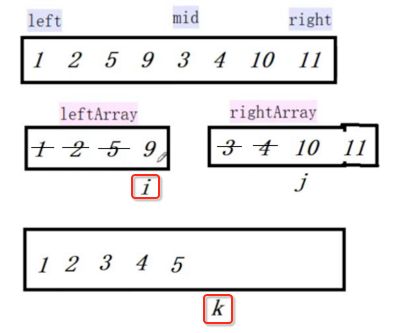
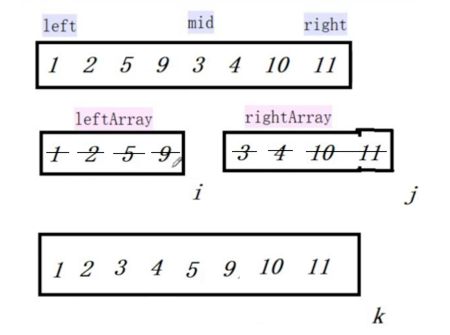
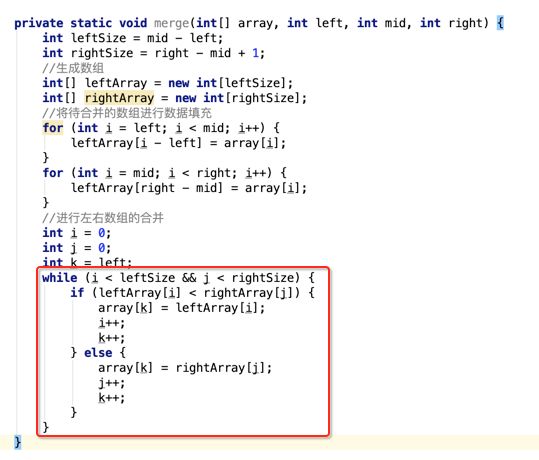
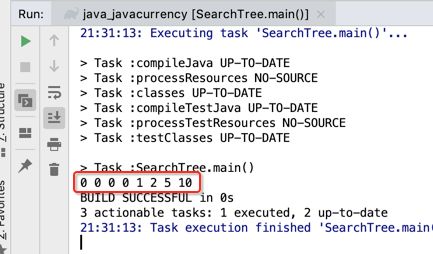
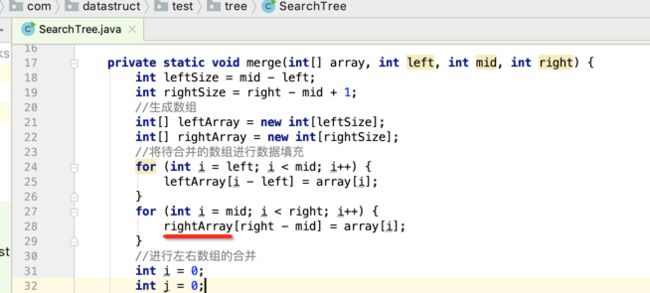
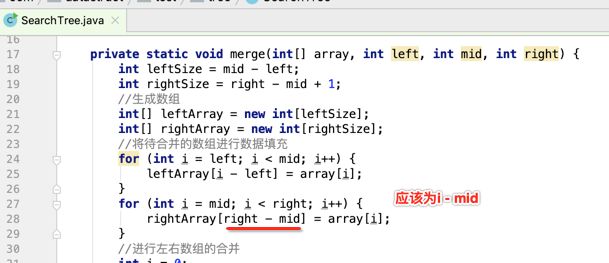
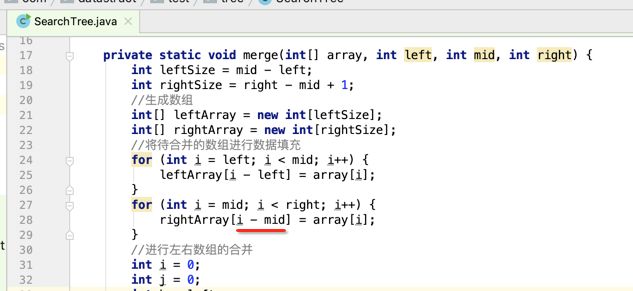
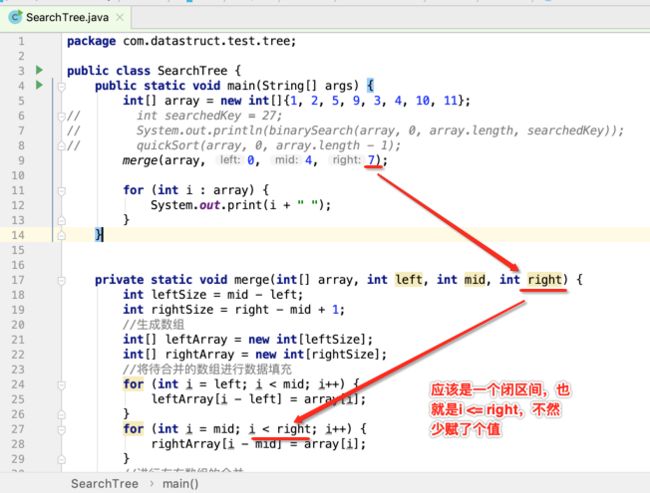
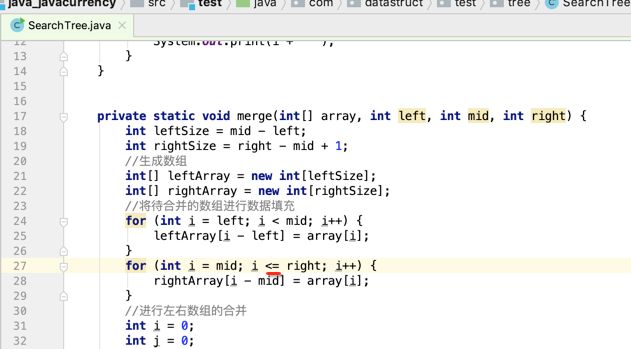
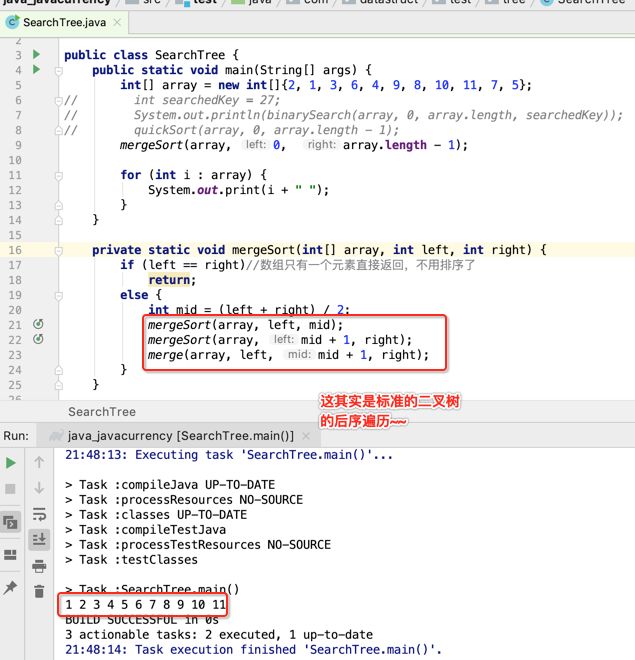
像JDK中的也有类似的思想：设计成左闭右开--是一种区间无重复的思想，比如：random(０，１)等大量的数学函数、for(int i=0;i

好，下面再来继续实现，比如容易理解：

再查一个找不到的值：

其实还有个小细节是在JDK中当找不到时不是返回的-1，而是写的最低位置，校仿一下：

快速排序（前序）：

其实在JDK中有快排的实现，如下：

其中里面的实现巨复杂，拿其中的一个排序方法来看：

当然它考虑的是比较完善的，而如果咱们自己来实现一个快排可以写得比较简练。

关于快排的思想，先用一个动画感受一下整个过程：

image.gif

是不是有点晕晕的，下面来一步步拆解上面演示的整个排序思路，略麻烦，但是此过程能让你对快排的思想了解得比较透：

先从第一位或者最后一位取一个值出来，这里取第一位：

然后用两个引用来表示第一位和最后一位，如下：

由于是从low位取的，所以对比则从high来对比，而76>31，所以high往左再移一下：

此时87>31，所以继续将high往左移一位：

此时12<31了，则将12取出来放到low的位置：

此时low再往右移一位：

此时68>31，则将其要放到high处：

此时high则往左开始移一格：

由于54>31，则继续往左移动：

39>31，继续往左移：

由于23<31，则将其放到low处：

此时low则往右移动一格了：

而45>31，则将其又放到high上，所以：

此时high往左移一格：

90>31，则high往左移：

当两引用重合时，则将31这个数放到重合的位置，所以最终31就排到了这里了：

此时有木有发现，31左边的数全是小于它的，而右边的数全是大于它的，那。。如果将所有的数据都让这种规则重做一遍是不是最终就达到了一个有序的数列了，这就是快速排序。

从上图中可以看出快速排序的时间复杂度O(n)=log2(n)，因为每一次最坏情况下都得进行n次的对比，好，下面再来用代码实现，先来确认第一个值：

然后取出第一位数，再定义low和begin引用：

再定义一个boolean的变量用来决定方向，因为会不断的来改变指针的移动方向，一下是高往低走，一下又是低往高走，所以：

但是有个事项需要注意，此时改变完方向之后要立马跳到while()循环外来，可能第一时间想到的用break，但是break之后代码还是继续会往下执行，比如：

由于目前在if..else..下面还木有写代码看得不是太明显，但是很明显我们不需要让它往下执行，所以此时需要用到标签了，如下用：

假如for循环木有进去，则需要让low和high引用进行重合，所以如下：

好，接下来else的写法把条件反过来依葫芦画瓢既可：

还有最后一步，将值放到重合的位置既可：

此时已经将一个数已经放好位置了，它左边的数都是小于它的，而右边的数都是大于它的，接下来则需要递归，将左右两边的数以此规则再次进行快速排序，其写法如下：

好，下面来验证一下是否如预期：

呃，有bug，为啥都输出1呢？其实是这块写得有问题：

应该是：

再运行：

有木有发现它其实就是树的前序遍历？

咱们再来看一下这个算法，其中条件相等的也会进行比较，如下：

短处：

1、如果当序列中有大量重复的数时，也会进行交互，其性能肯定是不太好的。

2、另外单向链式结构处理性能不好（一般来说，链式都不使用）。

应用场景：

数据量大并且是线性结构。

归并排序（后序）：

既然在上面快递排序有两大短板，那归并排序就能解决这些短板。所以它的特征是：

应用场景：

数据量大并且有很多重复数据，链式结构。

短处：

需要空间大。

关于这个排序其思想是先分再合，如下：

好，接下来咱们先来写合并的过程，一步步来，先将左右故意整成有序的数列，如下：

然后再将数组分别填在新建的两个数组中：

接着来做合并：

其合并的这三个变量代表：

然后整个合并的过程是这样的：

首先i的元素1

然后i也往前挪一位：

同样的还是比i和j元素谁小，谁就放到k的位置，所以i位置上的2放到k的位置，然后k再往前挪一位，i也往前挪一位：

继续以此类拟，由于此时的i>j，所以再将3放到k的位置：

由于规则类似就不多说了，再将4取到k处：

再取5：

再取9：

此时有个情况出现了，就是i已经超出了左边数组的边界了，那接下来怎么合呢，比较简单，一股脑的将另一个数组所剩下的所有元素挪过来既可，此时我们就发现就已经对两个数组进行了归并排序了，如下：

所以有了合并的思想之后，接下来咱们实现一下：

好，接下来得处理空出来的元素，如下：

以上是整个合并的代码逻辑，下面来验证一下看是否能将其数组进行归并排序？

然后运行看结果：

呃，程序有问题，没有按预期有序输出结果。。其实确实是有bug，如下：

另外，下标也不对：

此时再运行：

最终再运行：

嗯，终于成功归并成有序的了，好，当左右是一个有序数列进行归并的逻辑已经写好了，但是实际实例应该不可能是左边和右边都是现成有序的，所以接下来则需要加上递归完整的处理，如下：

整个思路就是先对左右进行排序，然后再进行左右归并处理，调用一下看最终结果是否如预期：

总结一下快速排序和归并排序：

1、都是用在数据量很大的情况下，其性能是最佳的。

2、快速排序只能排线程的结构，并且没有大量重复的数据元素存在。

3、归并排序是用空间换时间，既能用在线程的结构，又能排链式的结构。

4、时间复杂度都是一样的O(n) = log2(n)。

转至

package com.example.jett.lsn_5_201205;

import org.junit.Test;

/**
 * Example local unit test, which will execute on the development machine (host).
 *
 * @see Testing documentation
 */
public class ExampleUnitTest {
    @Test
    public void addition_isCorrect() throws Exception {
        int[] array=new int[]{1,7,4,9,3,2,6,5,8};
        int key=35;
        quickSort(array,0,array.length-1);

//        System.out.println(binarySearch(array,0,array.length,key));
        for (int i : array) {
            System.out.print(i+" ");
        }
    }
    /**
     * 二分查找
     */
    public static int binarySearch(int[] array,int fromIndex,int toIndex,int key){
        int low=fromIndex;
        int high=toIndex-1;
        while(low<=high){
            int mid=(low+high)/2;//取中间
            int midVal=array[mid];
            if(key>midVal){//去右边找
                low=mid+1;
            }else if(keylow;i--){
                    if(array[i]<=x){
                        array[low++]=array[i];//先赋值，后++（指针移动）
                        high=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                high=low;//如果上面的if从未进入，让两个指针重合
            }else{
                for(int i=low;i=x){
                        array[high--]=array[i];
                        low=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                low=high;
            }
        }
        //把最后找到的值 放入中间位置
        array[low]=x;
        //开始完成左右两边的操作
        quickSort(array,begin,low-1);
        quickSort(array,low+1,end);
    }
    @Test
    public void test(){
        int[] array=new int[]{2,1,6,4,3,9,8,10,7,5};
//        merge(array,0,4,7);
        mergeSort(array,0,array.length-1);
        for (int i : array) {
            System.out.print(i+" ");
        }
    }
    public static void mergeSort(int array[],int left,int right){
        if(left==right){
            return;
        }else{
            int mid=(left+right)/2;
            mergeSort(array,left,mid);
            mergeSort(array,mid+1,right);
            merge(array,left,mid+1,right);
        }
    }

    //    0    4   7
    //    1  2  5  9 === 3  4  10  11
    public static void merge(int[] array,int left,int mid,int right){
        int leftSize=mid-left;
        int rightSize=right-mid+1;
        //生成数组
        int[] leftArray=new int[leftSize];
        int[] rightArray=new int[rightSize];
        //填充数据
        for(int i=left;i