CV中的特征融合SFAM、ASFF、BiFPN、Hyper column

1、SFAM

SFAM（尺度特征聚合模块）在端到端的one-stage目标检测器M2Det中提出，M2Det利用主干网络和MLFPN进行特征提取，然后与SSD类似，根据学到的特征，产生密集的bounding box和类别得分，再利用NMS产生最后的位置和类别预测结果。MLFPN包括三个模块：FFM（特征融合模块），TUM（瘦U型模块），SFAM（尺度特征聚合模块）。

先看MLFPN的整体流程：

FFMv1通过融合主干的特征图将语义信息扩充成基本特征。每一个TUM模块生成一组多尺度的特征，然后通过交替连接的多个TUM和FFMv2模块提取多层次多尺度特征。最后，SFAM模块通过一个尺度级联的特征操作和一个自适应的注意机制将特征聚集到多层次的特征金字塔中。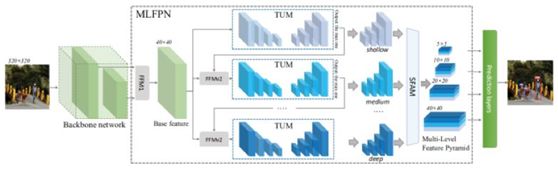

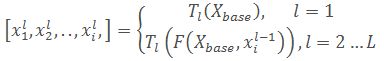
其中Xbase表示基础特征，$x_i^l$表示第$i$个尺度下第$l$个TUM模块得到的特征，$L$表示TUM模块的数量，$F$表示FFM模块。最后，SFAM模块通过尺度级联操作和基于通道域的注意机制来聚合多级多尺度特征。

FFMs(Feature Fusion Module)：
在M2Det中，FFM模块融合来自不同层的特征，使用1x1卷积层来压缩输入特征的通道，并使用维度相加操作来聚合这些特征。特别的，FFMv1将主干网络提取的两个不同尺度的特征作为输入，因此需要将深层次的特征先进行上采样，再进行维度的相加，同时，FFMv2模块接收基础特征和上一个TUM模块中的最大特征作为输入，这两个特征尺度是一致的，产生送入下一个TUM模块的融合特征。下图的（a）就是FFMv1操作，（b）是FFMv2操作。

TUMs(Thinned U-shape Module)：
与FPN和RetinaNet不同，TUM是利用一个瘦长U型网络构建的，我们知道，U型网络分为编码器和解码器部分，在编码器部分，进行的是一系列步长为2的3x3卷积；解码器部分进行上采样和特征元素求和操作后，添加1x1卷积层，以增强学习能力，保持特征的平滑。每个TUM中解码器部分的输出构成了当前层的多尺度特征。从整体上看，堆叠TUM模块的输出形成了多层次、多尺度的特征，而前面的主要是浅层特征，中向的主要是中层特征，后向的主要是深层特征。

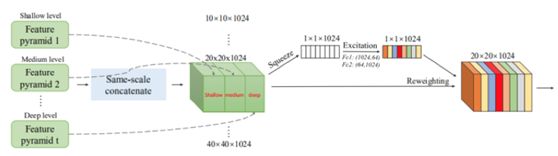
SFAM(Scale-wise Feature Aggregation Module)：
SFAM模块的目标是将TUMs生成的多层次多尺度特征聚合成多层次的特征金字塔。第一个步骤就是将不同TUM产生的相同尺度的特征进行通道叠加，叠加后的通道可以表示为：
$X=[X_1,X_2,\dots ,X_i]$
其中，X表示不同尺度下的特征图，具体表示为：
$X_i=Concat(X_i^1,X_i^2,\dots ,X_i^L,)\in R^{W_i\times H_i\times C}$
在这里，聚合特征金字塔的每一个尺度都包含来自不同层的相同尺度特征。

第二个步骤是引入了一个基于通道域的注意力机制来激励特征聚焦在对检测帮助最大的通道，这里引入了SENet的block，在挤压阶段，利用全局池化生成通道信息Z，为了完全捕获信道依赖，下面的激励步骤通过两个全连接层来学习注意力机制：
$s=F_{ex}(z,W)=\sigma (W_2\delta (W_{1}z))$
其中，$\sigma$表示ReLU操作，$\delta$表示Sigmoid
最后，将得到的激励s与输入$X$中的通道相乘，得到最终的输出：

SFAM总体结构为下图：

paper地址：https://arxiv.org/abs/1811.04533
GitHub地址：https://github.com/qijiezhao/M2Det

2、 ASFF

一种新的基于数据驱动的金字塔特征融合策略，自适应空间特征融合（ASFF）。自适应空间特征融合不同于以往的基于元素和或级联的多层次特征融合方法，我们的核心思想是自适应地学习各尺度特征地图融合的空间权重。文章：https://arxiv.org/pdf/1911.09516.pdf

它由两个步骤组成：相同的重新缩放和自适应融合，功能调整。我们将水平l（l∈{1,2,3}对于YOLOv3）的分辨率特征表示为$x^l$。对于级别l，我们将另一个级别$n$（$n\ne l$）的特征$x^n$调整为与xl相同的形状。由于YOLOv3中三个级别的特征具有不同的分辨率和不同的通道数，因此我们相应地修改了每个尺度的上采样和下采样策略。对于上采样，我们首先使用1×1卷积层将特征的通道数压缩到l级，然后分别使用插值来提高分辨率。对于1/2比例的下采样，我们简单地使用一个3×3的卷积层（步长为2）来同时修改通道数和分辨率。对于1/4的比例，我们在2步卷积之前添加了一个2步最大池层。
自适应融合。设$x^n\to l_{ij}$表示在位置$（i，j）$处的特征向量从$n$映射到$l$级。在相应的$l$级融合特征，如下所示:

以ASFF-3为例，图中的绿色框描述了如何将特征进行融合，其中$X^1$，$X^2$，$X^3$分别为来自level1，level2，level3的特征，与为来自不同层的特征乘上权重参数${\alpha }^3$，${\beta }^3$和${\gamma }^3$并相加，就能得到新的融合特征ASFF-3，如下面公式所示：
$y_{ij}^l={\alpha }_{ij}^l{x}_{ij}^{1\to l}+{\beta }_{ij}^l{x}_{ij}^{2\to l}+{\gamma }_{ij}^l{x}_{ij}^{3\to l}$

因为采用相加的方式，所以需要相加时的level1~3层输出的特征大小相同，且通道数也要相同，需要对不同层的feature做upsample或downsample并调整通道数。对于需要upsample的层，比如想得到ASFF3，需要将level1调整至和level3尺寸一致，采用的方式是先通过1×1卷积调整到与level3通道数一致，再用插值的方式resize到相同大小；而对于需要downsample的层，比如想得到ASFF1，此时对于level2到level1只需要用一个3×3，stride=2的卷积就可以了，如果是level3到level1则需要在3×3卷积的基础上再加一个stride=2的maxpooling，这样就能调整level3和level1尺寸一致。

对于权重参数$\alpha$，$\beta$和$\gamma$，则是通过resize后的level1~level3的特征图经过1×1的卷积得到的。并且参数α，β和γ经过concat之后通过softmax使得他们的范围都在[0,1]内并且和为1：

文章通过梯度和反向传播来解释为什么ASFF会有效。首先以最基本的YOLOv3为例，加入FPN后通过链式法则我们知道在backward的时候梯度是这样计算的：

其中因为不同尺度的层之间的尺度变换无非就是up-sampling或者down-sampling，因此$\partial x_{ij}^{1\to l}/\partial x_{ij}^1$这一项通常为固定值，为了简化表达式我们可以设置为1，$\partial x_{ij}^{1\to l}/\partial x_{ij}^1\approx 1$,则上面的式子变成了：

进一步的，$\partial y_{ij}^1/\partial x_{ij}^1$这一项相当于对输出特征的activation操作，导数也将为固定值，同理$\partial y_{ij}^l/\partial x_{ij}^{1\to l}$，我们可以将他们的值简化为1，则表达式进一步简化成了：

假设level1$（i,j）$对应位置feature map上刚好有物体并且为正样本，那其他level上对应$（i,j）$位置上可能刚好为负样本，这样反传过程中梯度既包含了正样本又包含了负样本，这种不连续性会对梯度结果造成干扰，并且降低训练的效率。而通过ASFF的方式，反传的梯度表达式就变成了：

可以通过权重参数来控制，比如刚才那种情况，另${\alpha }^2$和${\alpha }^3$=0，则负样本的梯度不会结果造成干扰。另外这也解释了为什么特征融合的权重参数来源于输出特征+卷积，因为融合的权重参数和特征是息息相关的
代码 ：

import torch
import torch.nn as nn
import torch.nn.functional as F

def add_conv(in_ch, out_ch, ksize, stride):
    """
    Add a conv2d / batchnorm / leaky ReLU block.
    Args:
        in_ch (int): number of input channels of the convolution layer.
        out_ch (int): number of output channels of the convolution layer.
        ksize (int): kernel size of the convolution layer.
        stride (int): stride of the convolution layer.
    Returns:
        stage (Sequential) : Sequential layers composing a convolution block.
    """
    stage = nn.Sequential()
    pad = (ksize - 1) // 2
    stage.add_module('conv', nn.Conv2d(in_channels=in_ch,
                                       out_channels=out_ch, kernel_size=ksize, stride=stride,
                                       padding=pad, bias=False))
    stage.add_module('batch_norm', nn.BatchNorm2d(out_ch))
    stage.add_module('leaky', nn.LeakyReLU(0.1))
    return stage
class ASFF(nn.Module):
    def __init__(self, level, rfb=False, vis=False):
        super(ASFF, self).__init__()
        self.level = level
        self.dim = [512, 256, 256]
        self.inter_dim = self.dim[self.level]
        if level==0:
            self.stride_level_1 = add_conv(256, self.inter_dim, 3, 2)
            self.stride_level_2 = add_conv(256, self.inter_dim, 3, 2)
            self.expand = add_conv(self.inter_dim, 1024, 3, 1)
        elif level==1:
            self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1)
            self.stride_level_2 = add_conv(256, self.inter_dim, 3, 2)
            self.expand = add_conv(self.inter_dim, 512, 3, 1)
        elif level==2:
            self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1)
            self.expand = add_conv(self.inter_dim, 256, 3, 1)

        compress_c = 8 if rfb else 16  #when adding rfb, we use half number of channels to save memory

        self.weight_level_0 = add_conv(self.inter_dim, compress_c, 1, 1)
        self.weight_level_1 = add_conv(self.inter_dim, compress_c, 1, 1)
        self.weight_level_2 = add_conv(self.inter_dim, compress_c, 1, 1)

        self.weight_levels = nn.Conv2d(compress_c*3, 3, kernel_size=1, stride=1, padding=0)
        self.vis= vis


    def forward(self, x_level_0, x_level_1, x_level_2):
        if self.level==0:
            level_0_resized = x_level_0
            level_1_resized = self.stride_level_1(x_level_1)

            level_2_downsampled_inter =F.max_pool2d(x_level_2, 3, stride=2, padding=1)
            level_2_resized = self.stride_level_2(level_2_downsampled_inter)

        elif self.level==1:
            level_0_compressed = self.compress_level_0(x_level_0)
            level_0_resized =F.interpolate(level_0_compressed, scale_factor=2, mode='nearest')
            level_1_resized =x_level_1
            level_2_resized =self.stride_level_2(x_level_2)
        elif self.level==2:
            level_0_compressed = self.compress_level_0(x_level_0)
            level_0_resized =F.interpolate(level_0_compressed, scale_factor=4, mode='nearest')
            level_1_resized =F.interpolate(x_level_1, scale_factor=2, mode='nearest')
            level_2_resized =x_level_2

        level_0_weight_v = self.weight_level_0(level_0_resized)
        level_1_weight_v = self.weight_level_1(level_1_resized)
        level_2_weight_v = self.weight_level_2(level_2_resized)
        levels_weight_v = torch.cat((level_0_weight_v, level_1_weight_v, level_2_weight_v),1)
        levels_weight = self.weight_levels(levels_weight_v)
        levels_weight = F.softmax(levels_weight, dim=1)

        fused_out_reduced = level_0_resized * levels_weight[:,0:1,:,:]+\
                            level_1_resized * levels_weight[:,1:2,:,:]+\
                            level_2_resized * levels_weight[:,2:,:,:]

        out = self.expand(fused_out_reduced)

        if self.vis:
            return out, levels_weight, fused_out_reduced.sum(dim=1)
        else:
            return out

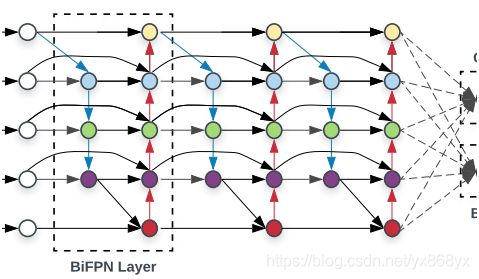
3、 BiFPN

BiFPN加权双向特征金字塔，在EfficientDet中提出。原文链接：https://arxiv.org/abs/1911.09070
BiFPN主要思想有两点：一是高效的双向跨尺度连接，二是加权特征图融合。

关于特征融合部分的结构设计，可以建模成如下问题：
给定一组输入特征$P{⃗}^{out}=(P_{l_1}^{in},P_{l_2}^{in},\dots )$，目标就是为了找到一个转化函数$f(.)$来聚合不同层的特征并输出一系列新的特征：$P{⃗}^{out}=f(P{⃗}^{in})$
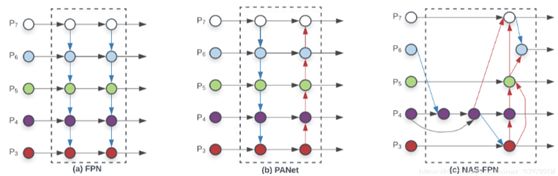
（a）中用图形表示了FPN的工作方式，FPN使用了top-down的方式，从网络深层不断将特征与前层特征进行结合。如图所示，其使用了$P_3$~$P_7$五个输入特征，$P_n$表示下采样n次得到的feature map，相应的尺寸为原图的$1⁄2^n$ 。
经典的FPN还可以通过下面的数学表示方式来表示：
$P_7^{out}=Conv(P_7^{in})$
$P_6^{out}=Conv(P_6^{in}+Resize(P_7^{out}))$
…
$P_3^{out}=Conv(P_3^{in}+Resize(P_4^{out}))$
其中，Resize表示上下采样过程，通常是为了对齐特征图尺寸；Conv表示卷积操作，为了抽取特征。

跨尺度连接

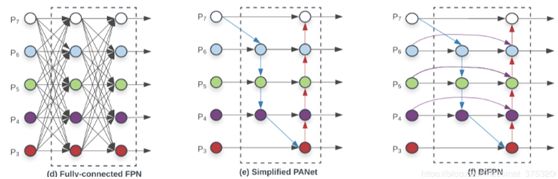
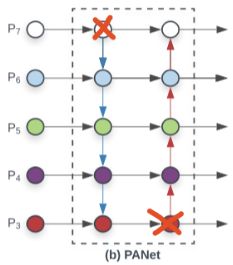
FPN（图a）只有一条top-down路径，PANet（图b）在其基础上又添加了bottom-up路径，而NAS-FPN搜索到了一个较稀疏的连接方式，但是过于抽象。作者对比这三者后发现，PANet效果最好，但带来了较大的参数量和计算量。因此，作者想在PANet的基础上，进行改进：

改进点一：删除入度为1的节点。因为直观认为，如果一个节点只有一个输入边且没有特征融合，那么它将对旨在融合不同特征的特征网络贡献较小。这样，我们从图(b)得到了图(e)。

改进点二：添加跳跃连接。如果原始输入和输出节点处于同一level，则在原始输入和输出节点之间添加一条额外的边，以便在不增加成本的情况下融合更多特征。 这样，我们得到了图(f)，也就是BiFPN的基本单元。

改进点三：将BiFPN视作一个基本单元，重复堆叠。不像PANet那样只有一个top-down和bottom-up路径，BiFPN将一对路径视为一个特征层，然后重复多次以得到更多高层特征融合。

加权特征融合
先前的特征融合方法大多平等地对待所有输入特征。然而，因为不同的特征具有不同的分辨率，他们对特征融合的贡献是不平等的。为解决此问题，本文提出在特征融合期间为每个输入添加一个额外的权重，让网络去学习每个输入特征的重要性。基于这种思想，作者试验了三种不同的加权方法：

无界融合

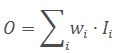
仅依靠一个标量就可以以最小的计算成本达到与其他方法相当的精度。但是，由于标量权重是无界的，容易导致训练不稳定，因此没有采用这种方法，而是采用了权重归一化来限制每个权重的范围

基于Softmax的融合方法

说到归一化权重，一个本能的想法就是使用Softmax，进而使得所有权重被标准化成一个0~1之间的概率值，以表征各个输入的重要性。然而，使用softmax会带来较大的GPU延迟。

快速归一化融合

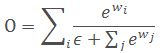
通过ReLU来保证各权重非负，通过添加一个很小的ϵ来保证数值稳定性。因为没有用到指数运算，所以速度较快。后续分解研究表明，这种融合方法较softmax融合具有非常相近的学习行为和准确性，但速度提高了30%。
代码：https://blog.csdn.net/jacke121/article/details/103323698

4、 Hyper column

超列（hypercolumn），指一个输入像素位置往后的所有对应位置的卷积网络单元激活值，组成一列向量。超列，借鉴于神经科学，其区别在于不仅仅指边缘检测器，还包含更多具有语义信息的神经单元。超列的idea，如下图所示：

超列的计算，十分简单。取得一个检测框（可能是正方形），resize到分类网络的固定输入大小（分类网络使用了全连接层），resized图像分块进入分类网络，把各个层的特征图进行bilinear插值，恢复到图像分块大小，取得各个层的对应位置的超列（级联多通道激活值）。
神经网络表示超列分类器，如下图所示

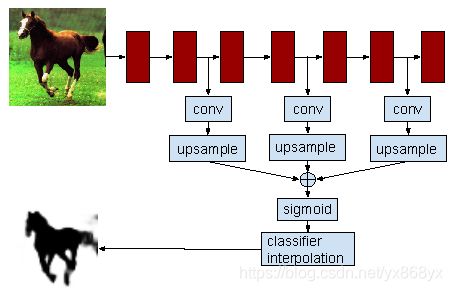
代码：http://blog.christianperone.com/2016/01/convolutional-hypercolumns-in-python/

参考博客：
https://blog.csdn.net/dQCFKyQDXYm3F8rB0/article/details/103708109
https://blog.csdn.net/dcxhun3/article/details/93891615
https://github.com/ruinmessi/ASFF/blob/master/models/yolov3_asff.py
https://blog.csdn.net/TJMtaotao/article/details/104473972
https://blog.csdn.net/TJMtaotao/article/details/103216377
https://github.com/ruinmessi/ASFF
https://blog.csdn.net/qq_36808245/article/details/103603020
https://blog.csdn.net/watermelon1123/article/details/103277773
https://blog.csdn.net/sinat_37532065/article/details/103317753
https://blog.csdn.net/dgyuanshaofeng/article/details/83904764
https://www.it610.com/article/4812523.htm
https://www.cnblogs.com/charlotte77/p/8343700.html