【NLP】n-gram LM & NN LM

n-gram LM

语言模型是生成模型，是一个泛泛的概念，通俗来讲，就是给定一句话的前半部分，预测生成剩余的部分。这里主要介绍一个简单的LM方法，n-gram。

任务描述

输入一个句子的开头单词：比如 I；

输出最有可能生成的完整的句子，比如：I love NLP.

假设S代表了整个句子，包含单词W1,W2,…，则我们的目标是逐个单词生成句子，使得最后的句子的概率P(S)最大。根据极大似然估计：

$$\max P(S)=\max P(W_1,W_2,...,W_N)=\max P(W_1)P(W_2|W_1)P(W_3|W_1,W_2)...P(W_N|W_1,...,W_{N-1})$$

模型结构

n-gram模型假设当前生成的单词只与其前面的n-1个单词有关，即：

$$\text{Bigram/2-gram: }P(W_1,W_2,...,W_N)=\prod _{i=2}^{N}P(W_i|W_{i-1})$$

$$\text{Trigram/3-gram: }P(W_1,W_2,...,W_N)=\prod _{i=3}^{N}P(W_i|W_{i-2},W_{i-1})$$

假设我们这里使用3-gram，那么问题转换成了如何求解每个3-gram对应的概率,假设我们有一个大训练集，里面包含了许多句子语料，那么我们可以根据统计来计算每个3-gram的概率：

$$P(W_3|W_1,W_2)=\frac{Count(W_1,W_2,W_3)}{Count(W_1,W_2)}$$

然后逐个生成句子的下一个单词。

Tricks

在 n-gram LM中有一些小技巧可以帮助提升模型的能力。

Smoothing

当语料库中语料不充分时会发生某些单词组合“0出现”的情况，如果不做提前处理，那么这些单词组合对应的概率都会为0，这显然是不对的，因为我们不能笼统的把未出现的单词的概率一改归结为0。此外，我们也需要保证上述通过count计算概率的公式中分母不为0。这个问题统称为数据稀疏问题。因此这里引入了“smoothing” 平滑技巧。 “smoothing”有很多种类，这里介绍几种常见的。

1. add-1 smoothing，V为预料中单词两两成对出现的种类数，可以把1换为alpha，则进阶成add-alpha smoothing：

$$P(W_3|W_1,W_2)=\frac{Count(W_1,W_2,W_3)+1}{Count(W_1,W_2)+V}$$

$$P(W_3|W_1,W_2)=\frac{Count(W_1,W_2,W_3)+\alpha }{Count(W_1,W_2)+\alpha V}$$

2. back-off 回退, 若n-gram出现次数为0，回退到(n-1)-gram。详细信息参考：https://en.wikipedia.org/wiki/Katz's_back-off_model。

3. Interpolation 插值，和回退类似，只不过回退是只有当n-gram出现为0时才回退到低阶gram，而插值法是直接将所有低阶线性组合起来。详细信息参考：https://blog.csdn.net/baimafujinji/article/details/51297802

Greedy Search vs Beam Search

假设我们使用3-gram，当我们已经得到各个3-gram的条件概率 $P(W_i|W_{i-2},W_{i-1})$ 时,我们怎么根据拥有的概率来选择下一步生成的单词呢？有两种方法：

1. Greedy Search，每一步都选择概率$P(W_i|W_{i-2},W_{i-1})$ 最大的Wi。这么做其实过于绝对，因为很可能下一步生成的单词本身的概率较小，但是当生成整个句子后，整个句子的概率却比较大。
2. Beam Search，第i步选择k个最可能的候选单词，然后第i+1步基于k个候选单词再生成新的单词，再选择k个最可能的，一直到生成句子末尾。可以参考：https://blog.csdn.net/pipisorry/article/details/78404964。

Log化乘为加

在计算 ${\prod }_{i=2}^{N}P(W_i|W_{i-1})$ 时，随着句子长度的增加，乘法会越来特多，计算量增大，我们可以使用log转换成连加，降低计算量 ${\sum }_{i=2}^N\log P(W_i|W_{i-1})$。

关于n-gram LM 可以参考《speech and language processing》。

NN LM

任务描述

同上

模型结构

除了n-gram LM 外， 神经网络也应用于LM。最初的NN LM只是一个简单的前向神经网络。结构如下：

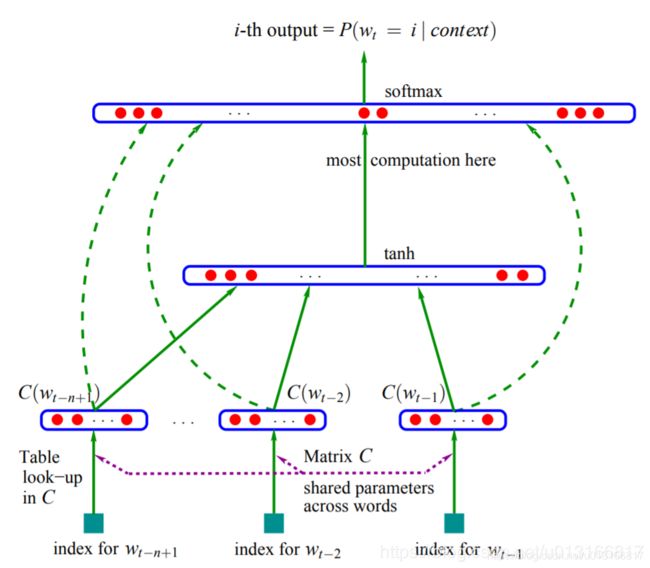
输入单词$w_t$的前几个单词的one-hot表示，经过word embedding（也可以看作是一种look-up），接着是一个tanh非线性，最后送到softmax输出概率$P(w_t|w_{t-n},....,w_{t-1})$。训练网络时的损失函数是：最小化负对数似然函数（通过交叉熵）：$\min [-\sum P(w_t|w_{t-n},....,w_{t-1})]$。优化方法可以使用梯度下降等。

NNLM相比于n-gram LM，优点在于：不需要整个语料库的统计信息，并且softmax本身已经具有smoothing的作用。（注意使用softmax之前要先减去最大值，防止数值向上/下溢出。）

DL vs ML

传统的NLP大多依赖于基于统计的ML，比如上面介绍的生成模型HMM，n-gram模型，此外比如未提到的NB模型和最大熵模型。而DL的发展也使得神经网络逐渐在NLP中处于主导地位，比如这一节的NN LM和下一节将介绍的RNN。那么传统ML 和 DL之间到底是什么关系呢？

1. ML 适合于小数据集，而DL则需要大量的数据来训练模型；
2. ML需要特征工程。而DL是一种end-to-end端到端的模型，可以理解为一个“黑盒子”，不需要特征工程；
3. 由于“黑盒子”的特性，DL模型很难被理解；而传统ML模型由于需要考虑特征，则更易于理解（比如SVM）；
4. 由于“端到端”特性，DL的适应性强，同一个模型不需要太多的调整就可以适用于不同的任务（比如迁移学习）；
5. DL由于大量的运算量，需要GPU的加持。
6. DL是大势。

Word Error Rate

$WER=\frac{S+D+I}{N}$，用来评估一个LM模型的好坏。

S：要替换的单词的数量

D：要被删除的单词的数量

I：要插入的单词的数量